Астронет > Звездные скопления

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Звездные скопления << 9.3 Движение звезд в поле регулярных сил сферического звездного скопления | Оглавление | 9.5 Время релаксации. Диссипация звездных скоплений >>

9.4 Иррегулярные силы. Максвеллово распределение скоростей. Теорема вириала. Динамические массы скоплений

В реальных звездных скоплениях время от времени происходят тесные сближения двух или нескольких звезд в процессе движения их по регулярным орбитам. При этом взаимные ускорения, испытываемые звездами, участвующими в сближениях, по порядку величины оказываются сравнимыми с ускорениями этих звезд, обусловленными действующей на них регулярной силой.

Силы, возникающие в результате звездных сближений, принято называть иррегулярными. Они действуют кратковременно и за время сближения меняют только относительные скорости участвующих в нем звезд. Они носят случайный характер в том смысле, что результат каждого сближения не зависит от результатов предыдущего.

Нарушая движение звезд по регулярным орбитам, иррегулярные силы в то же время устанавливают статистическое распределение остаточных скоростей звезд, т. е. распределение, подчиняющееся некоторому статистическому закону (под остаточными скоростями в данном случае подразумеваются скорости звезд относительно центра масс скопления). Если при этом действии иррегулярных сил все характеристики скопления остаются неизменными с течением времени, то говорят, что скопление находится в состоянии статистического равновесия или в статистически стационарном состоянии. Звездные сближения в скоплениях играют ту же роль, что и столкновения молекул в газах, благодаря которым в газах устанавливается наивероятнейший статистический закон распределения скоростей Максвелла. Используя методы статистической механики, звездная динамика показывает, что при достаточно большом числе звезд наивероятнейшим законом распределения их остаточных скоростей в статистически стационарном скоплении является тот же закон Максвелла:

$dN = N\left(\frac{j}{\sqrt\pi}\right)^3\exp(-j^2[v_\xi^2 + v_\eta^2 + v_\zeta^2])dv_\xi dv_\eta dv_\zeta ,$ (9.16)

где dN - число звезд в элементе объема пространства скоростей dv_ξdv_ηdv_ζ, N - полное число звезд скопления, v_ξ, v_η, v_ζ - компоненты остаточных скоростей v звезд,

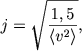
$j = \sqrt{\frac{1,5}{\langle v^2 \rangle}},$ (9.17)

а $\sqrt{\langle v^2 \rangle}$ - средняя квадратичная скорость звезд скопления, характеризующая дисперсию скоростей этих звезд. Символом 〈〉 здесь и в дальнейшем мы будем обозначать среднее значение. Если проинтегрировать выражение (9.16) по бесконечно тонкому сферическому слою в пространстве скоростей, то получится иная форма записи закона Максвелла:

$n(v)dv = \frac{4Nj^3}{\sqrt\pi}e^{-j^2v^2}v^2dv.$ (9.18)

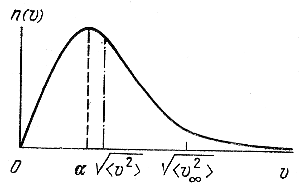
здесь n(v)dv - число звезд, скорости которых заключены n интервале от v до v+dv. График соответствующей кривой n(v) изображен на рис. 140. Максимум ее соответствует наиболее вероятной скорости α, связанной с параметром j соотношением α = j^-1, а со средней квадратичной скоростью - соотношением $\sqrt{\langle v^2 \rangle} = \sqrt{1,5}\alpha = \approx 1,22\alpha$ .

Рис. 140. Схематическое представление максвеллова закона распределения скоростей.

В статистически стационарном скоплении $\sum\limits_{i \ne j} m_im_jr_{ij}^2 = const$ . Из тождества Лагранжа - Якоби (9.8) в этом случае вытекает, что

$2E - \Omega = 0; \quad 2T + \Omega = 0.$ (9.19)

Это так называемая теорема вириала: в статистически стационарной системе ее потенциальная энергия, взятая с противоположным знаком, равна удвоенной кинетической энергии ее членов, а удвоенная полная энергия равна потенциальной. В статистически стационарном звездном скоплении средняя квадратичная скорость звезд связана с его массой М. Эта связь вытекает из теоремы вириала. Для простоты допустим, что все члены скопления имеют одинаковые массы m. Тогда М = Nm,

$2T = M\langle v^2 \rangle,$ (9.20)

а соотношение (9.2) можно записать в виде

$\Omega = -\frac{1}{2}\frac{Gm^2N(N-1)}{\bar R},$ (9.21)

где

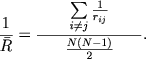
$\frac{1}{\bar R} = \frac{\qquad\sum\limits_{i \ne j}\frac{1}{r_{ij}}\qquad}{\frac{N(N-1)}{2}}.$ (9.22)

Величина $\bar R$ может быть названа средним эффективным радиусом скопления. Ее обратная величина является средним значением обратных величин взаимных расстояний между всеми членами скопления. Практически за $\bar R$ принимают радиус окружности, содержащей в проекции на плоскость половину массы скопления (Кинг, 1958а). Пренебрегая при большом N единицей в числителе выражения (9.21) и принимая во внимание соотношения (9.19), (9.20) и (9.21), находим

$\langle v^2 \rangle = \frac{1}{2}\frac{GM}{\bar R}.$ (9.23)

Если выразить М в единицах массы Солнца, а $\bar R$ - в парсеках, то

$\sqrt{\langle v^2 \rangle} = 0,0463\sqrt{\frac{M}{\bar R}} \, \mbox{км/с}.$ (9.24)

По этой формуле, зная значения М и $\bar R$ , можно определять дисперсию скоростей звезд в скоплении, а определив из наблюдений дисперсию скоростей и величину $\bar R$ , найти массу скопления М. Можно предложить и другие модификации формулы (9.24), зависящие от принятого закона распределения плотности звезд (или массы) в скоплении (см.,например, Курт, 1951).

В ядрах типичных рассеянных скоплений дисперсия скоростей звезд близка к ± 0,5 км/с. В частности, для Плеяд (Титус, 1938), она составляет ± 0,59 км/с, а для скопления Ясли (Схилт, Титус, 1938) ± 0,79 км/с. Соответствующие значения масс этих скоплений оказываются равными 510 и 730 масс Солнца (Минер, 1939; ван Вейк, 1949).

Сходные значения дисперсии скоростей звезд в этих скоплениях получил Джонс (1970а; 1970б; 1971), нашедший несколько более рафинированным методом, что соответствующая наблюдаемой дисперсии масса Плеяд достигает 690, а масса скопления Ясли - 560 масс Солнца.

Дисперсия лучевых скоростей звезд в шаровых скоплениях оказывается на порядок выше (Вилсон, Коффин, 1954; Шварцшильд, Бернстейн, 1955; Фист, Тэккерей, 11)60; Хардинг, 1965). Но ошибки лучевых скоростей слабых звезд, определявшихся до недавнего времени, были столь велики, что найденные перечисленными авторами значения дисперсии могли рассматриваться лишь как верхние пределы значений истинных дисперсий (Гунн, Гриффин, 1979). Правда, Хардинг (1965) по своим измерениям обнаружил даже вращение скопления ω Сеn, но, по-видимому, лишь в работах Иллингворса (1976), а также Да Косты и др. (1977), были получены надежные значения дисперсий скоростей звезд в ядрах нескольких шаровых скоплений.

Гунн и Гриффин (1979), используя фотоэлектрический спектрометр для измерения лучевых скоростей звезд, пoзволяющий определять их с точностью до 0,3 км/с, сумели не только определить дисперсию лучевых скоростей звезд в скоплении М 3 ( ± 4,8 км/с), но и проследить за ее уменьшением с увеличением расстояния от центра скопления, что свидетельствует об анизотропии поля скоростей во внешних областях этой системы. Анализ этих наблюдений и сочетании с анализом различных моделей скоплении, основанных на наблюдаемом распределении его поверхностной яркости, позволил им оценить значение полной массы М 3 (6 · 10⁵ масс Солнца) с большей точностью, чем это можно было бы сделать с помощью формулы (9.24).

Измерения Гунна и Гриффина, проведенные для 111 звезд скопления ярче 14^m,0 V, показали также отсутствие спектрально-двойных систем среди красных гигантов в М 3 и наличие случайных движений в атмосферах этих звезд со скоростями, достигающими нескольких десятых километра в секунду.

Существование максвеллова распределения скоростей с его "хвостом", уходящим в бесконечность, позволяет считать, что хотя и малая, но конечная доля полного числа звезд, скопления может приобретать скорости, достаточные для преодоления притяжения со стороны остальных членов системы. Наименьшая скорость, при которой звезда навсегда покидает изолированное скопление, называется параболической скоростью, или скоростью освобождения, отрыва от скопления. Обозначим ее символом v_∞. Для того, чтобы звезда покинула скопление, ее кинетическая энергия T_∞, должна быть не меньше энергии ее гравитационного взаимодействия с остальными звездами скопления, т. е. взятой с обратным знаком ее потенциальной энергии. Обозначим средние значения этих энергий символами 〈T_∞〉 и 〈Ω;;;_i〉. Условие равенства соответствующих величин приводит к соотношению

$\langle v_{\infty}^2 \rangle = \frac{2GM}{\bar R}.$ (9.25)

Сравнивая (9.23) с (9.25), находим, что

$\sqrt{\langle v_{\infty}^2 \rangle} = 2\sqrt{\langle v^2 \rangle},$ (9.26)

т. е. средняя квадратичная скорость освобождения равна удвоенному значению средней квадратичной скорости звезд в скоплении (см. рис. 140). Теоретически в условиях строгого статистического равновесия должно соблюдаться равнораспределение кинетической энергии между членами скопления, имеющими разные массы:

$m_1\langle v^2(m_1) \rangle = m_2\langle v^2(m_2) \rangle,$ (9.27)

Расчеты на ЭВМ, имитирующие динамическую эволюцию системы (Вилен, 1967), показывают, однако, что в предоставленной самой себе системе гравитационно взаимодействующих n тел с разными массами равнораспределение кинетической энергии не сохраняется. Об этом же свидетельствуют и наблюдения. Так, в Плеядах дисперсия скоростей не возрастает заметно с переходом к звездам меньших масс (Джонс, 1970а).

Следующим важным понятием, на которое опирается статистическая теория динамики звездных скоплений, является понятие времени релаксации.

<< 9.3 Движение звезд в поле регулярных сил сферического звездного скопления | Оглавление | 9.5 Время релаксации. Диссипация звездных скоплений >>

Публикации с ключевыми словами: звезды - Скопление
Публикации со словами: звезды - Скопление

См. также:

Черная дыра разрушает звезду: анимация

Звезды, пыль и туманность в NGC 6559

25 самых ярких звезд на ночном небе

Анимация: черная дыра разрушает звезду

Комета, скопления и туманности

Сравнение размеров звезд

Самая далекая из всех известных звезд?

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце