Астронет > Звездные скопления

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Звездные скопления << 9.2 Основные уравнения и общие интегралы движения. Тождество Лагранжа - Якоби | Оглавление | 9.4 Иррегулярные силы. Максвеллово распределение скоростей. Теорема вириала. Динамические массы скоплений >>

9.3 Движение звезд в поле регулярных сил сферического звездного скопления

Если пренебречь действием иррегулярных сил (влиянием близких и далеких сближений звезд с другими членами скопления), можно определить траекторию звезды, описываемую ею под действием регулярной силы, обусловленной сглаженным гравитационным полом всего скопления. Эту траекторию иногда называют регулярной орбитой. Рассмотрим регулярные орбиты звезд в сферическом скоплении, концентрирующемся к центру. Решение задачи сводится к анализу движения материальной точки с массой m вокруг точки с переменной массой M(r) (см., например, Э. Стремгрен, 1916).

Если f(r) - пространственная плотность звезд в скоплении на расстоянии r от его центра, то масса скопления, заключенная в сфере радиуса r,

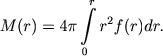
$M(r) = 4\pi\int\limits_0^r r^2 f(r)dr.$ (9.9)

Если f(r) изменяется по закону Шустера (8.33), то, принимая в нем для простоты f(0) = 1, r₀ = 1, можно написать

$f(r) = \frac{1}{(1+r^2)^{5/2}}.$ (9.10)

В таком случае M(r) легко вычисляется по формуле

$M(r) = \frac{4\pi}{3}\frac{r^3}{(1+r^2)^{3/2}},$ (9.11)

сила K(r), притягивающая звезду m к центру такого скопления, изменяется по закону

$K(r) = \frac{GmM(r)}{r^2} = \frac{4\pi}{3}\frac{Gmr}{(1+r^2)^{3/2}},$ (9.12)

Теперь можно написать систему дифференциальных уравнений движения и проинтегрировать ее.

Получаемые при этом регулярные орбиты звезд имеют вид эллипсов с вращающимися линиями апсид (рис. 139). Возможны также устойчивые круговые орбиты и движения по прямым, проходящим через центр масс скопления. Плоскости орбит во всех случаях проходят через центр.

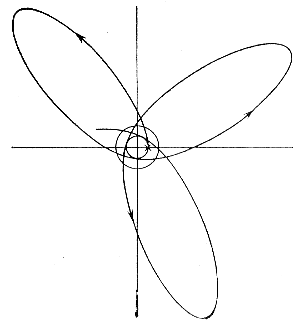
Рис. 139. Регулярная орбита звезды в шаровом скоплении (Э. Стремгрен, 1916).

Точное решение уравнений движения звезды оказывается возможным также в более общем случае так называемых изохронных скоплений, рассмотренных, в частности, Эноном (1959а; 1959б; 1960а). Потенциал таких скоплений определяется выражением

$\Phi (r) = \frac{(2r^2 + 1 - \sqrt{4r^2 + 1})}{2r^2}.$ (9.13)

В общем случае орбитальный период звезды в скоплении зависит от ее полной энергии Е и углового момента. В изохронном скоплении он зависит только от величины Е. Пространственная плотность f(r) при этом находится из выражения

$4\pi Gf(r) = \frac{2[1-\Phi (r)]^4[3+\Phi (r)]}{[1+\Phi (r)]^3},$ (9.14)

а видимая F(r) - по формуле

$4\pi GF(r) = \frac{1}{r^3} \left(\arctg 2r - \frac{2r}{1+4r^2} \right).$ (9.15)

Наблюдаемое распределение F(r) в шаровых скоплениях М 5, М 15, М 92, ω Сеn и 47 Тuс неплохо представляется формулой (9.15). Орбиты звезд в изохронных скоплениях сходны с изображенной на рис. 139. Обобщенные изохронные модели скоплений были предложены Велтманном (1965б), а также Кузминым и Велтманном (1972). На их описании мы уже не можем останавливаться.

<< 9.2 Основные уравнения и общие интегралы движения. Тождество Лагранжа - Якоби | Оглавление | 9.4 Иррегулярные силы. Максвеллово распределение скоростей. Теорема вириала. Динамические массы скоплений >>

Публикации с ключевыми словами: звезды - Скопление
Публикации со словами: звезды - Скопление

См. также:

Черная дыра разрушает звезду: анимация

Звезды, пыль и туманность в NGC 6559

25 самых ярких звезд на ночном небе

Анимация: черная дыра разрушает звезду

Комета, скопления и туманности

Сравнение размеров звезд

Самая далекая из всех известных звезд?

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце