8.9 Общие законы распределения плотности в звездных скоплениях. Закон Шустера. Закон Кинга
Неоднократно делались попытки найти общие законы распределения плотности в звездных скоплениях. Как правило, при этом рассеянные и шаровые скопления рассматривались раздельно. Первые поиски общего закона распределения пространственной плотности звезд в звездных скоплениях были связаны с представлением о возможности проведения аналогии между звездными скоплениями и газовыми шарами. Пламмер (1911; 1916) аппроксимировал распределение плотности f(r), наблюдаемое в ярких шаровых скоплениях, изученных Пиккерингом (1897) и Бэйли (1916), законом Шустера, предложенным последним для представления внутреннего строения звезд:
|
|
(8.33) |
где r0 - некоторая постоянная. Популярности этого закона, по справедливому замечанию Костицына (1922), немало способствовала его простота. Поскольку закон Шустера - Пламмера удовлетворял наблюдениям далеко не всегда (Цейпель, 1913; Костицын, 1922), возникла необходимость его обобщения, впервые предложенного Валленквистом (1933):
|
|
(8.34) |
где β - постоянная, могущая меняться от скопления к скоплению. Согласно Ломану (1964), рассмотревшему распределение плотности в 67 рассеянных скоплениях по данным Валленквиста (см. ниже), в 80% случаев оно удовлетворительно представляется законом (8.34) при 2,0 < р < 4,4.
В 1959 г. Валленквист (1959) опубликовал результаты своей почти тридцатилетней работы по изучению структуры 67 рассеянных скоплений. Его исследование относится, в сущности, как мы теперь знаем, только к ядрам скоплений и даже в ряде случаев лишь к внутренним зонам этих ядер (за исключением Гиад). Для однородности исследования он подсчитывал звезды в пределах четырех величин, начиная от самых ярких.
Валленквист нашел, что распределение пространственной плотности в ядрах всех скоплений лучше всего представляется законом
|
|
(8.35) |
где расстояние от центра r выражается в долях радиуса скопления (вернее, в долях радиуса ядра), принятого Валленквистом: 0 ≤ 1 - r ≤ 1.
Постоянная с называется степенью концентрации. При с = 0 f(r) не зависит от r и равна центральной плотности f(0). Чем больше с, тем быстрее изменяется f(r), тем сильнее концентрируются звезды в ядре скопления к его центру.
Корреляции величин с с классами концентрации Трюмплера (1930а) не обнаружено. По-видимому, как и в случае шаровых скоплений, невозможно сравнивать реальные количественные показатели степени концентрации с простыми оценками этой величины, основанными на непосредственном зрительном восприятии внешнего вида системы. Наиболее существенной закономерностью, обнаруженной Валленквистом, является увеличение степени концентрации звезд в ядре скопления к его центру с увеличением линейных размеров ядра, что связано, очевидно, с ростом массы последнего.
Перейдем теперь к рассмотрению работы Кинга (1962), которому удалось, по-видимому, найти действительно общий эмпирический закон распределения видимой плотности звезд в звездных скоплениях (как шаровых, так и рассеянных.) и карликовых эллиптических галактиках.
Оказалось, что видимая плотность F(r) во внешних частях проекции шаровых звездных скоплений па небесную сферу, исправленная за плотность звезд фона, меняется с изменением r по закону
|
|
(8.36) |
где F1 = const, a rt - значение r, при котором F(r) = 0. На графике ![]() мы должны получить прямую линию. Нa рис. 134 (Кинг, 1962) изображен ход F(r) по подсчетам звезд в шаровом скоплении М 15. Мы видим, что закон (8.36) хорошо соблюдается в наружных областях скопления. Пересечение получаемой прямой линии с осью абсцисс определяет радиус скопления rt, при котором F(r) достигает нуля.
мы должны получить прямую линию. Нa рис. 134 (Кинг, 1962) изображен ход F(r) по подсчетам звезд в шаровом скоплении М 15. Мы видим, что закон (8.36) хорошо соблюдается в наружных областях скопления. Пересечение получаемой прямой линии с осью абсцисс определяет радиус скопления rt, при котором F(r) достигает нуля.
Уклонения от закона (8.36) на рис. 134 заметны при 1/r > 1,5; для центральных частей скоплений он явно неприменим, так как там он приводит к бесконечно большим значениям плотностей, и нужно искать другой закон.
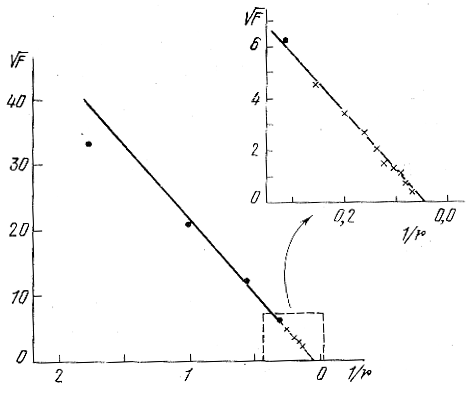
Рис. 134. Проверка закона (8.36) по подсчетам звезд во внешних
областях скопления М 15 (Кинг, 1962).
Анализируя данные поверхностной фотометрии Гаскойна и Барра (1956) для скопления 47 Тuс, о которых мы уже говорили, Кинг пришел к выводу, что распределение поверхностной яркости F(r) в этом случае можно представить формулой
|
|
(8.37) |
где F0 - центральная поверхностная яркость, а rс - так называемый масштабный множитель, который Кинг называет радиусом сердцевины (core) скопления. Как отмечает Кинг, радиус rс определяется внутренней энергией системы, а радиус rt - внешними приливными силами. В свое время Моубрэй (1946) определил для 64 шаровых скоплений диаметры d0,5 их изображений, при которых поверхностная яркость падает до половины центральной поверхностной яркости системы. Значения rс близки к ½d0,5. Эти значения не соответствуют значениям радиусов ядер скоплений, определение которых дано нами в § 8.4. Так, например, для скопления М 3 мы принимаем, что радиус ядра равен 5',3. Соответствующее значение d0,5 Моубрэя составляет 0',7.
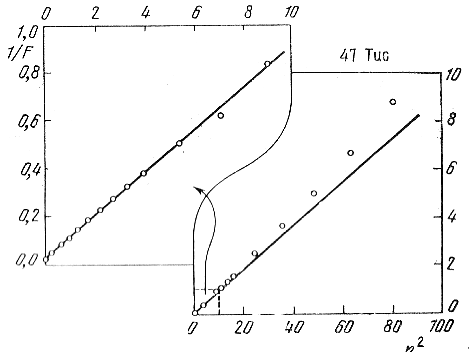
Рис. 135. Проверка закона (8.37) по распределению поверхностной яркости в центральной области скопления 47 Тuс (Кинг, 1962).
В сущности, как подчеркивают Петерсон и Кинг (1975), гс является радиусом области почти постоянной плотности близ центра скопления, т. е. радиусом центральной зоны ядра, по нашей терминологии (см. § 8.4). В самом деле, радиус, центральной зоны ядра скопления М 3 по нашим данным равен 0',5, что близко к приведенному выше значению 0',7 или к половине его. Если откладывать по оси ординат 1/F, а по оси абсцисс r2, то на графике должна получиться прямая линия. На рис. 135 (Кинг, 1962) изображен ход поверхностной яркости в центральной области скопления 47 Тuс. От 0 до 5' наблюдения достаточно хорошо согласуются с законом (8.37). Соотношение же (8.36) удовлетворяет в данном случае наблюдениям от границ скопления до 2' от его центра.
Позже Кинг (1966б) опубликовал результаты фотоэлектрической поверхностной фотометрии внутренних областей девяти ярких шаровых скоплений, подтвердившие правильность формулы (8.37). Единая формула, объединяющая свойства обеих формул и представляющая распределение плотности во всем скоплении, имеет вид
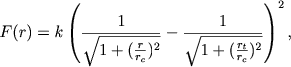
|
(8.38) |
В типичном шаровом скоплении rt/rc ≈ 30. Если r/rc мало или не очень велико, то, вынося в (8.38) первый член за скобки, получаем выражение (8.37) с
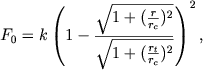
|
где разность в скобках не очень сильно отличается от 1. Выражение (8.38) можно записать также в виде
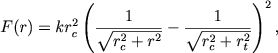
|
(8.39) |
показывающем, что при r 》 rc и rt 》 rc оно переходит в выражение (8.36) с F1 = krc2.
Для сравнения закона (8.38) с наблюдениями Кинг построил стандартные кривые lgF(r) для разных значений логарифма параметра с = rt/rc, который можно называть просто концентрацией. Эти кривые изображены на рис. 136 и 137 (Кинг, 1962). Рис. 136 удобен для анализа распределения плотности во внутренних областях скоплений, рис. 137 - во внешних.
Значения с заключены в пределах от 3,5 до 125. Они довольно хорошо коррелируют с тремя классами концентрации излучения, найденными Кроном и Мейаллом (1960). Чем больше значение с, тем выше концентрация звезд к центру системы. В то же время, как и следовало ожидать, корреляция этого параметра с классами концентрации Шепли - Сойер и Моубрэя (см. § 2.3) очень слаба.
Результаты подсчетов звезд и кривые lgF(r), lgr для 54 шаровых скоплений приведены в статье Кинга и др. (1968), а еще для 23 скоплений - в статье Петерсона (1976). Значения rt и rc для большого числа скоплений можно найти в статьях Петерсона и Кинга (1975), а также Петерсона (1976), в которых в качестве параметра концентрации с принимается уже не значение rt/rc, a lg(rt/rc).
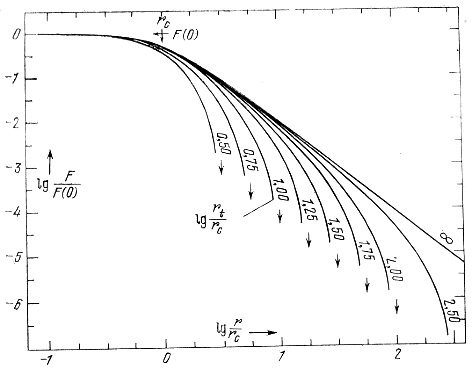
Рис. 136. Кривые распределения видимой плотности во внутренних областях скоплений для разных значений параметра концентрации
с (Кинг, 1962).
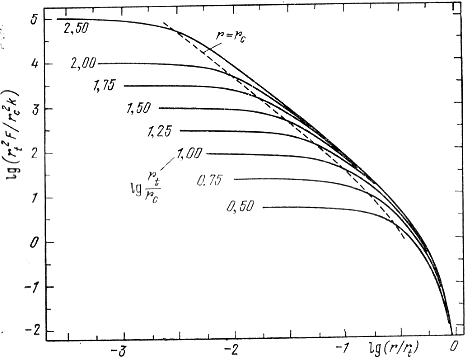
Рис. 137. Кривые распределения видимой плотности во внешних областях скоплений для разных значений параметра концентрации
с (Кинг, 1962).
Сравним рис. 136 и 137 с рис. 128 и 129 (см. § 8.6). Хотя в первом; случае мы имеем дело с кривыми F(r), а во втором - с f(r), рисунки очень сходны. Формулы (8.21) и рис. 120 показывают, что значения f(r) ≈ 0,1F(r). Несомненно, как те, так и другие кривые иллюстрируют одни и те же закономерности строения звездных скоплений. Кривые Кинга, естественно, более сглажены.
По аналогии с обобщением закона Шустера Велтманн (1965а) предложил своеобразное обобщение формулы Кинга (8.38):
![$$
F(r) = F_0 \left(\frac{1}{[1+(\frac{r}{r_0})^{\gamma}]^{\beta / k}} - \frac{1}{[1+(\frac{r_t}{r_0})^{\gamma}]^{\beta / k}}\right)^k,
$$](https://images.astronet.ru/pubd/2011/06/28/0001252610/tex/formula215.gif)
|
(8.40) |
где k, β, γ - некоторые постоянные. Соотношение (8.40) переходит в (8.38)) при k = 2, β = 1, γ = 2. Однако вряд ли формула (8.40) применялась на практике при других значениях постоянных.
Кинг (1962) нашел также общий закон распределения пространственной плотности f(r) во всем скоплении путем подстановки выражения (8.38) в решение уравнения Абеля (8.7):
|
|
(8.41) |
Этот закон используется при проведении исследований, посвященных динамике звездных скоплений.
Еще один закон распределения плотности, - в так называемых изохронных скоплениях, - будет рассмотрен в следующей главе (§ 9.3) в связи с описанием динамических свойств звездных скоплений, неразрывно связанных с их структурными особенностями.
В заключение - несколько замечаний о кубоидальных звездных скоплениях (см. Карсдем, 1974). До сих пор не удалось обнаружить ни одного такого скопления. Поэтому Карсдем не нашел никаких признаков того, что эти скопления концентрируются к галактической плоскости, а также пришел к не совсем, правда, убедительному выводу, что вся совокупность данных об этих объектах не подтверждает весьма распространенную гипотезу об образовании звезд из облаков межзвездной среды.
<< 8.8 Анализ распределения поверхностной яркости в шаровых скоплениях. Кривые концентрации излучения | Оглавление | 9.1 Вводные замечания >>
|
Публикации с ключевыми словами:
звезды - Скопление
Публикации со словами: звезды - Скопление | |
См. также:
Все публикации на ту же тему >> | |