Звездные скопления
<< 8.7 Процентное содержание звезд разных типов в ядрах и коронах скоплений | Оглавление | 8.9 Общие законы распределения плотности в звездных скоплениях. Закон Шустера. Закон Кинга >>
8.8 Анализ распределения поверхностной яркости в шаровых скоплениях. Кривые концентрации излучения
В § 8.1 мы уже упоминали о работе Схилта (1928), проанализировавшего эллиптичность ω Сеn методом фотографической поверхностной фотометрии. С появлением электрофотометрии этот метод, естественно, уступил место фотоэлектрическому, впервые примененному Гаскойном и Барром (1956) к скоплениям ω Сеn и 47 Тuс.
Анализ распределения излучения в звездном скоплении может привести к результатам, совпадающим с результатами звездных подсчетов, только в том случае, если мы уверены в тождественности радиального распределения звезд разной светимости, иными словами, если функция светимости звезд в скоплении не зависит от расстояния от его центра.
В случае рассеянных скоплений это заведомо не имеет места. Достаточно обратиться к рис. 131, чтобы убедиться и том, что в центрах рассеянных скоплений распределение поверхностной яркости определяется плотностью их наиболее массивных ярких звезд, а на периферии - распределением более многочисленных и менее массивных слабых. Анализ радиального распределения поверхностной яркости в таком случае не сможет дать реальной картины распределения масс или пространственной плотности звезд в данном скоплении.
Однако в случае шаровых скоплений, если их поверхностная яркость определяется звездами более яркими, чем звезды верхнего конца главной последовательности, имеющими, по современным представлениям, почти одинаковые массы, такой анализ может дать сведения о реальном распределении пространственной звездной плотности в системе. Правда, и в этом случае, поскольку мы уже знаем о явлениях быстрой потери массы звездами при переходе с верхнего конца ветви гигантов на горизонтальную ветвь, можно предвидеть осложнения в интерпретации наблюдаемой картины, если скорость динамической эволюции подсистемы звезд, потерявших массу, окажется достаточной для заметного изменения распределения плотности в этой подсистеме за время сохранения ее членами соответствующих физических характеристик.
Большой интерес представляют проведенные Кроном и Мейаллом (1960) с помощью электрофотометра, снабженного набором диафрагм, наблюдения 187 шаровых и рассеянных скоплений в нашей Галактике, Магеллановых Облаках, системе Печи и галактиках М 31, М 33, NGC 185 и NGC 205. Наблюдения велись в системах Р, V, I. Для каждого скопления были получены интегральные величины Vi, для 117 - интегральные показатели цвета Р - V и V - I, а для 77 - значения угловых диаметров d0,9, в пределах которых заключено 0,9 интегрального излучения скопления.
Для каждого скопления, измерявшегося через диафрагмы с различными отверстиями, строились графики Δ m, 5 lgd (рис. 133), где d - диаметр отверстия, выраженный в минутах дуги. Если бы яркость в каждой точке видимого диска скопления была постоянной, то приращения видимой величины скопления Δ m с переходом к диафрагме большего диаметра были бы пропорциональны приращениям lgd. В самом деле, количество излучения I, проходящего через диафрагму, пропорционально площади ее отверстия: I ∝ πd2, откуда lgI ∝ lgd, но Δ lgI ∝ Δ m, следовательно, Δ (lgd) ∝ Δ m. Так как, однако, яркость дисков скоплений падает к краю, то с удалением от центра скопления данному приращению величины 5 lgd соответствует меньшее приращение Δ m, причем тем меньшее, чем быстрее падает яркость, чем сильнее излучение концентрируется к центру системы. Поэтому кривые, изображенные на рис. 133, можно назвать кривыми концентрации излучения. Нетрудно видеть, что их форма зависит лишь от закона распределения яркости по диску скопления и не зависит от размеров скопления и расстояния до него.
Взаимное сравнение этих кривых показало, что около 80% всех наблюдавшихся скоплений можно разбить на три класса по степени центральной концентрации излучения: а - малая концентрация, b - средняя, с - высокая (см. рис. 133). При отсутствии концентрации (диск равномерной яркости) кривая превращается в прямую; чем сильнее концентрация, тем больше кривизна кривых.
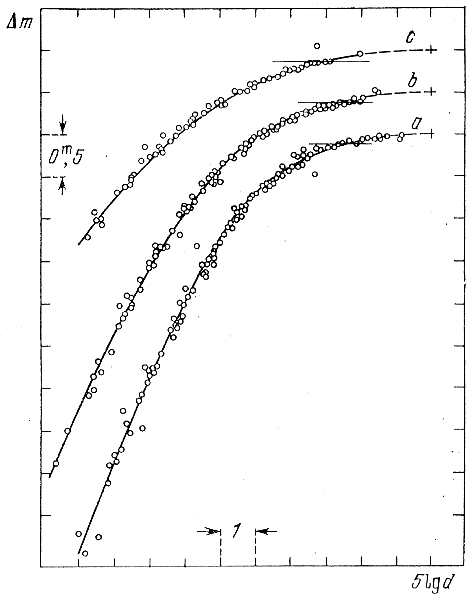
Рис. 133. Кривые концентрации излучения (Крон, Мейалл, 1960).
Корреляция между классами концентрации шаровых скоплений по Шепли и Сойер и классами концентрации получения практически отсутствует. Так, например, скопление М 13 (V класса концентрации) относится к классу a, а скопление М 15 (практически того же - IV класса концентрации) - к классу c. Возвращаясь к рис. 126, отметим, что скопление М 2 относится к классу a, скопление М 3 - к классу b, и еще рано связывать наличие колебаний плотности в объеме скопления с классом его концентрации.
<< 8.7 Процентное содержание звезд разных типов в ядрах и коронах скоплений | Оглавление | 8.9 Общие законы распределения плотности в звездных скоплениях. Закон Шустера. Закон Кинга >>
|
Публикации с ключевыми словами:
звезды - Скопление
Публикации со словами: звезды - Скопление | |
См. также:
Все публикации на ту же тему >> | |
