Астронет > Звездные скопления

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Звездные скопления << 9.1 Вводные замечания | Оглавление | 9.3 Движение звезд в поле регулярных сил сферического звездного скопления >>

9.2 Основные уравнения и общие интегралы движения. Тождество Лагранжа - Якоби

Рис. 138. Схема, поясняющая вывод формул (9.1) - (9.4).

Рассмотрим уравнения движения звезд в изолированном звездном скоплении, состоящем из n звезд с разными массами m₁, m₂, ..., m_n. Пусть r_ij - расстояние между двумя из них, имеющими массы m_i и m_j (рис. 138). По закону Ньютона они притягиваются друг к другу с силой Gm_im_ir_ij^-2. На звезду m_i со стороны звезды m_j действует сила с компонентами $-Gm_i m_j(x_i - x_j)r_{ij}^{-3}, \quad -Gm_i m_j(y_i - y_j)r_{ij}^{-3}, \quad -Gm_i m_j(z_i - z_j)r_{ij}^{-3}$ . Эти компоненты можно выразить через величину $\Omega_{ij} = -Gm_im_jr_{ij}^{-1}$ , т. е. потенциальную энергию звезды m_i относительно звезды m_j: $-\frac{\partial\Omega_{ij}}{\partial x_i}, \quad -\frac{\partial\Omega_{ij}}{\partial y_i}, \quad -\frac{\partial\Omega_{ij}}{\partial z_i}$ . Все звезды скопления действуют на звезду m_i с силой, компоненты которой равны $-\frac{\partial\Omega_{i}}{\partial x_i}, \quad -\frac{\partial\Omega_{i}}{\partial y_i}, \quad -\frac{\partial\Omega_{i}}{\partial z_i}$ , где

$\Omega_i = \sum\limits_j \Omega_{ij} = -Gm_i \sum\limits_j \frac{m_j}{r_{ij}}$ (9.1)

при j ≠ i, Ω;;;_i - потенциальная энергия звезды m_i.

Потенциальная энергия всего скопления, т. е. энергия взаимного притяжения всех звезд скопления,

$\Omega = -G \sum\limits_{i \ne j} \frac{m_im_j}{r_{ij}}$ (9.2)

где суммирование производится по всем различным парам звезд. Нетрудно видеть, что

$\Omega = \frac{1}{2}\sum\limits_i \Omega_{i}.$ (9.3)

Дифференциальные уравнения движения звезд скопления имеют вид

$m_i \ddot x_i = -\frac{\partial\Omega}{\partial x_i}, \quad m_i \ddot y_i = -\frac{\partial\Omega}{\partial y_i}, \quad m_i \ddot z_i = -\frac{\partial\Omega}{\partial z_i},$ (9.4)

где i = 1, 2, ..., n. Интегрируя систему этих уравнений, можно получить 10 общих интегралов движения, т. е. соотношений, связывающих между собой искомые функции x_i(t), y_i(t), z_i(t) и принимающих постоянное значение, если в них вместо неизвестных функций подставить решение системы. Шесть из них - интегралы движения центра масс скопления, показывающие, что в абсолютной системе координат он движется равномерно и прямолинейно в некотором направлении. Три из них - это интегралы площадей или угловых моментов:

$\sum\limits_i m_i(y_i\dot z_i - z_i\dot y_i) = c_1, \quad \sum\limits_i m_i(z_i\dot x_i - x_i\dot z_i) = c_2, \quad \sum\limits_i m_i(x_i\dot y_i - y_i\dot x_i) = c_3,$ (9.5)

где с₁, с₂, с₃ - постоянные. Наконец, десятый интеграл - это интеграл энергии

$\frac{1}{2}\sum\limits_i m_i (\dot x_i^2 + \dot y_i^2 + \dot z_i^2) + \Omega = h,$ (9.6)

где h - постоянная энергии, означающий, что во время движения изолированной системы полная энергия ее Е, являющаяся суммой кинетической (T) и потенциальной энергии (Ω;;;), остается постоянной.

Если рассматривать движение звезд скопления относительно центра его масс, имеющего координаты $\bar x, \, \bar y, \, \bar z$ и ввести координаты звезд относительно этого центра $\xi_i = x_i - \bar x, \, \eta_i = y_i - \bar y, \, \zeta_i = z_i - \bar z$ , то для описания движения останутся только три интеграла площадей и интеграл энергии, которые примут вид

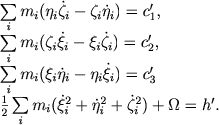
$\begin{array}{l} \sum\limits_i m_i (\eta_i\dot \zeta_i - \zeta_i\dot \eta_i) = c'_1, \\ \sum\limits_i m_i (\zeta_i\dot \xi_i - \xi_i\dot \zeta_i) = c'_2, \\ \sum\limits_i m_i (\xi_i\dot \eta_i - \eta_i\dot \xi_i) = c'_3 \\ \frac{1}{2}\sum\limits_i m_i (\dot \xi_i^2 + \dot\eta_i^2 + \dot \zeta_i^2) + \Omega = h'. \end{array}$ (9.7)

Кроме того, в этой системе отсчета всегда удовлетворяется так называемое тождество Лагранжа - Якоби

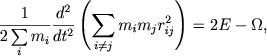
$\frac{1}{2\sum\limits_i m_i}\frac{d^2}{dt^2}\left(\sum\limits_{i \ne j} m_i m_j r_{ij}^2\right) = 2E - \Omega,$ (9.8)

из которого можно извлечь необходимое условие устойчивости звездного скопления. В самом деле, величина Ω;;; всегда отрицательна; следовательно, если Е > 0, то 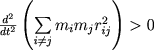$\frac{d^2}{dt^2}\left(\sum\limits_{i \ne j} m_i m_j r_{ij}^2\right) > 0$ , т.е выражение 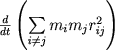$\frac{d}{dt}\left(\sum\limits_{i \ne j} m_i m_j r_{ij}^2\right)$ неограниченно возрастает с течением времени. Даже если оно первоначально было отрицательным, то через некоторое время станет положительным, и величина $\sum\limits_{i \ne j} m_i m_j r_{ij}^2$ начнет возрастать. Это значит, что по крайней мере одно из расстояний r_ij будет стремиться к бесконечности.

Таким образом, необходимым (но не достаточным) условием устойчивости звездного скопления является отрицательность его полной энергии: Е < 0. Если Е > 0, система не может быть динамически устойчивой, стационарной.

Пользуясь методами классической небесной механики для описания общих динамических свойств скоплений, мы можем опираться только на приведенные выше интегралы площадей, энергии и тождество Лагранжа - Якоби, дающие лишь самое общее представление об этих свойствах. Чтобы получить более конкретные представления о динамической эволюции скоплений, можно идти двумя путями. Первый из них - это применение к звездным скоплениям методов статистической физики, второй - численное интегрирование с помощью ЭВМ строгих уравнений движения n тел при разных начальных условиях.

В первом случае используется понятие фазовой плотности системы, т. е. функции распределения числа ее членов в единице объема фазового шестимерного пространства (координат и скоростей) как функции времени, удовлетворяющей уравнению Больцмана (см., например, Огородников, 1958, с. 243).

Несмотря на большие успехи, достигнутые на пути использования ЭВМ, возможности ЭВМ еще ограничены, и с их помощью до сих пор удается строго анализировать поведение систем, число членов которых n ≲ 500 (Вилен, 1974). Поэтому по-прежнему продолжается развитие статистических методов решения проблемы, результаты применения которых неплохо согласуются с результатами, полученными с помощью ЭВМ.

Прежде чем перейти к описанию статистических методов, рассмотрим движение звезд в поле регулярных сил скопления, определяемом только его потенциалом.

<< 9.1 Вводные замечания | Оглавление | 9.3 Движение звезд в поле регулярных сил сферического звездного скопления >>

Публикации с ключевыми словами: звезды - Скопление
Публикации со словами: звезды - Скопление

См. также:

Черная дыра разрушает звезду: анимация

Звезды, пыль и туманность в NGC 6559

25 самых ярких звезд на ночном небе

Анимация: черная дыра разрушает звезду

Комета, скопления и туманности

Сравнение размеров звезд

Самая далекая из всех известных звезд?

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце