Астронет > Звездные скопления

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Звездные скопления << 9.4 Иррегулярные силы. Максвеллово распределение скоростей. Теорема вириала. Динамические массы скоплений | Оглавление | 9.6 Изотермические ядра скоплений. Определение относительных масс звезд в звездных скоплениях >>

9.5 Время релаксации. Диссипация звездных скоплений

Под временем релаксации скопления τ в звездной динамике принято подразумевать промежуток времени, в течение которого в системе под действием иррегулярных сил успевает восстановиться нарушенное максвеллово распределение скоростей. Чем больше τ, тем меньше влияние звездных сближений на движение звезд скопления. На практике для нахождения τ вводятся различные определения этого понятия. В результате сближения двух звезд наблюдается отклонение направлений их движения от первоначальных и обмен кинетическими энергиями Δ E между ними. В динамике звездных систем (см., например, Чандрасекар, 1948) показывается, как можно получить формулы для вычисления величины &Sigma(Δ E)² для одной звезды и определить зависимость этой величины от времени t. Когда величина $\sqrt{\langle \Sigma (\Delta E)^2 \rangle}$ становится сравнимой с начальной кинетической энергией звезды, мы говорим, что время τ_E, необходимое для этого, есть время релаксации скопления. Можно дать и другие определения времени релаксации, например, оценить время τ_D, в течение которого &Sigma sin²φ, где φ - угол отклонения звезды при рассматриваемом сближении от первоначального направления движения, становится равной 1. При всех таких определениях значения τ_E, τ_D и т. п. оказываются величинами одного порядка. По Чандрасекару (1948), с поправкой Спитцера и Херма (1958),

$\tau = 0,1357\sqrt{\frac{N\bar R^3}{Gm}}\frac{1}{\ln \frac{N}{2}},$ (9.28)

где N - число звезд в скоплении, $\bar R$ - его средний эффективный радиус, определяемый соотношением (9.22), m - масса звезды, принимаемая одинаковой для всех членов скопления, G - постоянная тяготения. Эта формула выведена путем использования средней дисперсии скоростей для всего объема скопления. Так как в действительности плотность в скоплении быстро убывает с удалением от его центра, сближения между звездами должны при этом происходить реже, становясь менее эффективными. Соответственно, в корональной области скопления время релаксации должно быть больше, чем в области ядра.

Кинг (1958а; 1958в; 1959) показал, что учет концентрации звезд к центру скопления при условии, что плотность в скоплении меняется по закону Шустера, приводит к замене числового множителя в выражении (9.28) на 0,35, т. е. увеличивает время релаксации скопления по сравнению с получаемым по формуле (9.28) в 2,6 раза.

Расчет показывает, что для ядра Плеяд, например, τ = 8 · 10⁷ лет. Так как возраст этого скопления близок к 2 · 10⁷ лет, можно думать, что в ядре его еще не успело установиться максвеллово распределение скоростей. Не исключено, однако, что время релаксации при образовании скопления, в момент начального коллапса системы (см. § 9.8), оказывается намного меньше времени релаксации, соответствующего нынешнему состоянию системы.

Пользуясь понятием времени релаксации, можно оценить скорость потери звезд скоплением. Звезды, находящиеся в "хвосте" максвеллова распределения, скорости которых превышают скорость отрыва, покидают скопление. Распределение скоростей, как говорят, является усеченным при скорости отрыва. Это явление имеет огромное значение для эволюции скоплений. Впервые оно было независимо рассмотрено Амбарцумяном (1938) и Спитцером (1940). Обозначим долю звезд скопления, находящихся в хвосте максвеллова распределения скоростей, скорости которых превышают параболическую, буквой K. Произведя соответствующее интегрирование, нетрудно найти, что K = 0,0074. Принимая, что по истечении времени релаксации τ максвеллово распределение восстанавливается и новые 0,74% звезд скопления приобретают скорости, превышающие скорость отрыва, можно найти долю звезд, покидающих скопление за единицу времени (K/τ); скорость потери звезд скоплением определится уравнением

$\frac{1}{N}\frac{dN}{dt} = -\frac{K}{\tau}.$ (9.29)

Полный распад скопления должен, как кажется, произойти за время, не превышающее τ/K. Однако реальная картина диссипации скопления, сопровождающей его динамическую эволюцию, намного сложнее.

Кинг (1958а) перечислил ряд факторов, влияющих на характер и темп диссипации, совместный учет которых еще невозможен. Некоторые из них уже упомянуты в § 9.1. Рассмотрим бегло остальные факторы, изученные в дальнейшем Кингом (1958б; 1958в; 1959; 1960).

Тесные сближения звезд, учитывавшиеся при первых исследованиях полей иррегулярных сил в скоплениях, происходят сравнительно редко. Значительную роль в перераспределении энергии между членами скопления играют слабые взаимодействия звезд, обусловленные их далекими сближениями, суммарное воздействие которых на движение данной звезды может быть очень существенным. Впервые этот эффект был учтен Чандрасекаром (1943а, б, в), который применил так называемое уравнение Фоккера - Планка для описания изменений, вносимых далекими звездными сближениями в распределение скоростей звезд.

Чандрасекар обратил внимание на то, что звезды, приобретшие скорость, превышающую скорость отрыва, не обязательно должны покинуть скопление, так как дальнейшие сближения могут затормозить их движение. Чандрасекар (1943а) ввел даже понятие "динамического трения", показав, что звезды, имеющие более быстрое движение относительно окружающих, в среднем замедляют свое движение. Кинг (1959) показал, что сближения уходящих звезд с остающимися увеличивают эффективное время релаксации на время, требующееся для того, чтобы уходящая звезда покинула скопление. Для массивных скоплений с большим временем релаксации этим эффектом можно пренебречь, но для скоплений с небольшим числом членов он увеличивает эффективное время релаксации на 10-30%. Следует иметь в виду также, что уход звезд из скопления происходит непрерывно, а не после того, как в хвосте максвеллова распределения накапливается нужный процент звезд со скоростями, превышающими параболическую.

Результаты Чандрасекара, связанные с учетом влияний далеких сближений, были уточнены Спитцером и Хермом (1958), а затем Кингом (1960).

С другой стороны, Энон (1960б) пришел к выводу, что далекие сближения не могут привести к приобретению звездой энергии, превышающей энергию отрыва, и вновь подчеркнул важность рассмотрения близких сближений для решения проблемы диссипации звездных скоплений, на порядок уменьшив величину скорости диссипации, найденную Кингом (1958а).

В связи с большой неопределенностью подобных оценок, расходящихся между собою иногда на два порядка, мы не будем останавливаться на описании других работ, посвященных этой проблеме; обзор многих из них можно найти в уже упоминавшейся статье Петровской (1968).

До сих пор мы подразумевали, что скопление состоит из звезд с одинаковыми массами. Однако массы членов реальных звездных скоплений различны. Некоторое представление о скорости диссипации звезд разных масс из звездных скоплений дают работы Спитцера и Херма (1958), Агекяна (1959), Энона (1961), Вулли и Диккенса (1962), а также Мичи (1963). Звезды, масса которых на порядок меньше средней массы звезд скопления, диссипируют из скопления в 15-30 раз быстрее звезд средней массы. Этому выводу, однако, противоречат результаты расчетов динамической эволюции моделей скоплений (Вилен, 1967), согласно которым процент звезд, покидающих сформировавшееся скопление, не зависит от их массы (см. § 9.8). Звезды значительно более массивные, чем звезды средней массы, практически не покидают скопления. Если они сохраняются в ядрах скоплений в виде черных дыр, их влияние на динамическую эволюцию скопления было бы трудно переоценить. Но, по-видимому, постепенно они все же выбрасываются из скоплений при кратных взаимных сближениях.

Еще Спитцер (1940) отметил, что в процессе динамической эволюции плотное изолированное скопление, теряя звезды, должно сжиматься. Количественно этот процесс был изучен Гуревичем и Левиным (1950), Кингом (1958б) и Хёрнером (1958). Рассмотрим ход рассуждений Кинга.

Из теоремы вириала (9.19) следует, что

$E = \frac{1}{2}\Omega$ (9.30)

и

$\frac{1}{E}\frac{dE}{dt} = \frac{1}{\Omega}\frac{d\Omega}{dt} = \frac{L}{\tau},$ (9.31)

где L - отношение энергии, уносимой уходящими звездами, находящимися в хвосте максвеллова распределения скоростей, к абсолютному значению полной энергии E. Так как E < 0, ее абсолютное значение возрастает. Из соотношения (9.21) с заменой множителя N-1 на N вытекает равенство

$\frac{1}{\Omega}\frac{d\Omega}{dt} = \frac{2}{N}\frac{dN}{dt} - \frac{1}{\bar R}\frac{d\bar R}{dt}.$ (9.32)

Исключая τ из соотношений (9.29), (9.31) и (9.32), находим

$\frac{d\bar R}{\bar R} = \left(2+\frac{L}{K}\right)\frac{dN}{N},$ (9.33)

откуда

$\frac{\bar R}{\bar R_0} = \left(\frac{N}{N_0}\right)^{2+\frac{L}{K}},$ (9.34)

где $\bar R_0$ и N₀ - начальные значения $\bar R$ и N соответственно. По этому закону уменьшается средний эффективный радиус изолированного скопления с уменьшением числа N остающихся в нем звезд.

Рассмотрим теперь, как меняется τ с изменением N. Соотношение (9.28) с поправками Кинга (1958а, в; 1959), описанными выше, принимает вид

$\tau = 0,35\sqrt{\frac{N\bar R^3}{Gm}}\frac{1}{\ln \frac{N}{2}}.$ (9.35)

Подставляя сюда $\bar R$ из соотношения (9.34), находим

$\tau = \tau_0\left(\frac{N}{N_0}\right)^p\frac{\ln \frac{N_0}{2}}{\ln \frac{N}{2}},$ (9.36)

где τ₀ есть начальное значение τ (при N = N₀, $\bar R$ = $\bar R_0$ ), а p = 7/2 + 3/2L/K.

Подстановка выражения (9.36) в (9.29) позволяет получить дифференциальное уравнение для определения зависимости N(t).

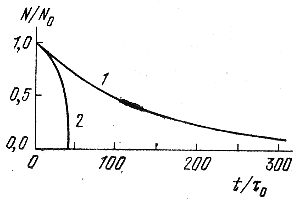
Рис. 141. Число звезд, остающихся в скоплении с течением времени (Кинг, 1958б).

На рис. 141 (Кинг, 1958б) показана полученная Кингом для N₀ = 250 и р = 7/2 кривая 2 изменения отношения N/N₀, с течением времени t/τ₀ в скоплении, плотность в котором меняется по закону Шустера. Процесс потери звезд идет с большим ускорением. Кривая 1, приведенная для сравнения на том же рисунке, соответствует экспоненциальному закону убывания числа звезд, который наблюдался бы в случае, если бы время релаксации оставалось постоянным.

Для очень широкого диапазона значений N₀, от 30 до 10 000, продолжительность существования рассматриваемого плотного изолированного скопления оказывается заключенной в очень узких пределах - от 44,7 τ₀ до 39,6 τ₀. Однако такие скопления встречаются только в воображении исследователей. Описанный выше процесс не учитывает наличия вокруг ядер скоплений массивных протяженных корональных областей, и его, строго говоря, можно отнести лишь к ядрам скоплений, которые, как уже неоднократно подчеркивалось нами, до сравнительно недавнего времени полностью отождествлялись с самими скоплениями. Достижение звездой скорости отрыва от ядра скопления вовсе не означает, что она может покинуть скопление. Выйдя из ядра, она может затормозиться в короне скопления и даже вновь вернуться в ядро. Таким образом, ускоренный распад ядра не означает ускоренного распада скопления в целом. Как показал позже тот же Кинг (1966а), изменивший свою точку зрения, обширная корона (называемая им оболочкой скопления), окружающая концентрированное ядро, препятствует потере звезд скоплением. Общая скорость потери звезд реальным скоплением практически не зависит от степени его концентрации к центру и определяется только полным числом членов скопления и действующей на скопление приливной силой, очень мало меняясь с течением времени.

<< 9.4 Иррегулярные силы. Максвеллово распределение скоростей. Теорема вириала. Динамические массы скоплений | Оглавление | 9.6 Изотермические ядра скоплений. Определение относительных масс звезд в звездных скоплениях >>

Публикации с ключевыми словами: звезды - Скопление
Публикации со словами: звезды - Скопление

См. также:

Черная дыра разрушает звезду: анимация

Звезды, пыль и туманность в NGC 6559

25 самых ярких звезд на ночном небе

Анимация: черная дыра разрушает звезду

Комета, скопления и туманности

Сравнение размеров звезд

Самая далекая из всех известных звезд?

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце