Астронет > Звездные скопления

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Звездные скопления << 9.5 Время релаксации. Диссипация звездных скоплений | Оглавление | 9.7 Динамическая эволюция звездных скоплений >>

9.6 Изотермические ядра скоплений. Определение относительных масс звезд в звездных скоплениях

При изучении звездных скоплений оказывается удобным и возможным пользоваться некоторыми терминами и выводами теории строения газовых шаров, например, понятием "температура". В газовых шарах температура определяется энергией движения молекул, в звездных скоплениях соответствующее понятие связано с энергией движения звезд. Рассмотрим максвеллово распределение скоростей (9.18). В газовых шарах роль параметра j² играет отношение m/2kT, где m - масса молекул, T - температура, k - постоянная Больцмана. Если T постоянна во всем объеме шара, то говорят об изотермическом газовом шаре. По аналогии можно говорить об "изотермическом" звездном скоплении, подразумевая под этим, что в нем повсюду господствует максвеллов закон распределения скоростей, причем параметр j этого закона всюду одинаков (т. е. дисперсия скоростей звезд данной массы всюду одинакова).

В самогравитирующей звездной системе потенциал Ф(r) и распределение звездной плотности f(r), отождествляемой в нашем случае с плотностью массы, связаны между собой уравнением Пуассона

$\frac{d^2\Phi (r)}{dr^2} + \frac{2}{r}\frac{d\Phi (r)}{dr} + 4\pi Gf(r) = 0.$ (9.37)

Вто же время в любом скоплении распределение f(r) определяется господствующим в нем распределением скоростей его членов. Поэтому изотермическое скопление должно иметь совершенно определенное строение, соответствующее закону

$f(r) = f(0)e^{-2j^2\Phi (r)}.$ (9.38)

Наблюдения показывают, что ни одно звездное скопление не является изотермическим во всем его объеме, хотя бы потому, что изотермическая газовая сфера имеет бесконечную массу, растущую пропорционально радиусу сферы. С достаточной степенью точности можно принять, что в состоянии изотермического равновесия находятся центральные области ядер скоплений, а во внешних частях плотность падает быстрее, чем если бы они представляла собой продолжение центральной изотермической сферы. Зная распределение плотности в изотермических ядра скоплений, можно теоретически обосновать возможность определения относительных масс звезд в звездных скоплениях (Хёрнер, 1957). Из соотношений (9.38) и (9.17) следует

$f(r) = f(0)e^{-\frac{3\Phi (r)}{\langle v^2 \rangle}}.$ (9.39)

При условии выполнения закона равнораспределения энергии (9.24) для звезд с массами m и m₀ можно написать

$\left. \begin{array}{l} f(r,m) = f(0,m)\exp[-\frac{3\Phi (r)m}{m_0 \langle v^2(m_0) \rangle}], \\ f(r,m_0) = f(0,m_0)\exp[-\frac{3\Phi (r)}{\langle v^2(m_0) \rangle}]. \end{array} \right\}$ (9.40)

Введем обозначения: m/m₀ = μ , g(r, m) = f(r, m)/f(0, m). Тогда

$g(r, m) = [g(r, m_0)]^\mu,$ (9.41)

$\lg g(r, m) = \mu\lg g(r, m_0)],$ (9.42)

или

$\lg f(r, m) = const + \frac{m}{m_0}\lg f(r, m_0).$ (9.43)

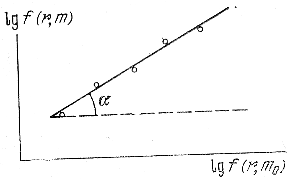
Рис. 142. Диаграмма относительных концентраций.

Если сопоставить между собой величины lgf(r, m) и lgf(r, m₀), соответствующие одним и тем же значениям r, то можно получить так называемую диаграмму относительных масс или относительных концентраций (рис. 142). Тангенс угла наклона α прямой, получающейся на этой диаграмме, равен μ, т. е. отношению масс звезд рассматриваемых групп. Этот метод определения относительных масс звезд в звездных скоплениях предложил и использовал еще Цейпель (1921).

К сожалению, ошибки в определении угла наклона прямой на рис. 142 очень велики (Холопов, 1955б). Этот наклон весьма чувствителен к выбору центра ядра скопления, к учету степени эллиптичности ядра. На рис. 143 (Хёрнер, 1957), показана зависимость масса - светимость ( $\mathfrak M$ , М_{p_v}) для звезд шаровых скоплений М 3 и М 92, полученная Хёрнером с помощью использования диаграмм относительных концентраций групп звезд разных абсолютных величин М_{p_v} в этих скоплениях. Здесь масса звезд $\mathfrak M$ выражена в единицах массы звезд с М_{p_v} = 0. Для сравнения показана зависимость масса - светимость для звезд в окрестностях Солнца по данным Салпитера (кривая а). Хёрнер считает, что ход зависимости для звезд скопления М 92 неплохо согласуется с результатами, предсказываемыми современной теорией эволюции звезд шаровых скоплений (кривая б). Соответствующая зависимость для звезд скопления М 3 хуже согласуется с этой теорией, но, учитывая большие ошибки определения относительных масс звезд по методу Цейпеля, следует признать, что и в этом случае нет оснований для беспокойства и отношении правильности упомянутой теории.

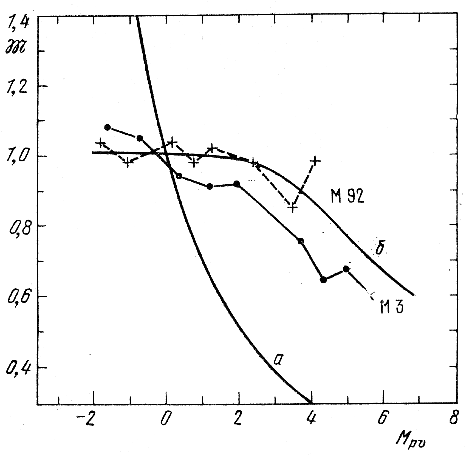
Рис. 143. Зависимость масса - светимость для звезд шаровых скоплений М 3 и М 92 (Хёрнер, 1957); а - зависимость масса - светимость для звезд в окрестностях Солнца, б - соответствующая теории эволюции зависимость для проэволюционировавшх звезд шаровых скоплений.

<< 9.5 Время релаксации. Диссипация звездных скоплений | Оглавление | 9.7 Динамическая эволюция звездных скоплений >>

Публикации с ключевыми словами: звезды - Скопление
Публикации со словами: звезды - Скопление

См. также:

Черная дыра разрушает звезду: анимация

Звезды, пыль и туманность в NGC 6559

25 самых ярких звезд на ночном небе

Анимация: черная дыра разрушает звезду

Комета, скопления и туманности

Сравнение размеров звезд

Самая далекая из всех известных звезд?

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

$g(r, m) = [g(r, m_0)]^\mu,$	(9.41)
$\lg g(r, m) = \mu\lg g(r, m_0)],$	(9.42)