<< 5.6 Поиски солнечных нейтрино | Оглавление | 6.2 Соотношение масса-светимость >>
6. Строение и устойчивость звезд
Subsections
- 6.1 Уравнения звездой структуры
- 6.2 Соотношение масса-светимость
- 6.3 Тепловая устойчивость звезд
- 6.4 Эволюция звезд главной последовательности
- 6.5 Горение гелия: 3
 -реакция
-реакция
- 6.6 Определение возраста скоплений
- 6.7 Качественная картина эволюции звезды
6.1 Уравнения звездой структуры
В самой общей постановке расчет внутреннего строения звезд сводится к интегрированию четырех дифференциальных уравнений, каждое из которых мы подробно рассматривали в предыдущих главах. Выпишем сейчас их вместе.
1. Уравнение массы:
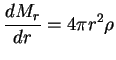 или
или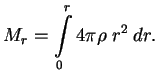
2. Уравнение гидростатического равновесия:
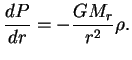
3. Уравнение переноса энергии в диффузионном приближении:
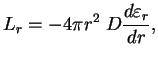
Перепишем это уравнение в виде
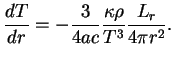
4. Уравнение энергетического баланса:
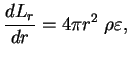
Эти дифференциальные уравнения следует дополнить уравнением состояния
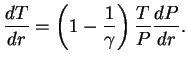
Только что обособившуюся в результате конденсации межзвездного газа звезду разумно
считать химически однородной. Как показывают расчет, эволюция звезды идет различными
путями в зависимости от того, остается ли звезда химически однородной или же
изменения химического состава происходят только там, где протекают ядерные
реакции, т. е. в ее центральных областях. У маломассивных звезд(
![]() )
конвекцией может быть охвачена большая часть звезды, поэтому здесь перемешивание
приводит к тому, что химический состав меняется у всей звезды в целом. У более
массивных звезд конвекция отсутствует вообще либо происходит в небольшой
центральной части, где выделяется энергия, и для них изменение химического состава
является функцией только лагранжевой координаты и пропорционально скорости выделения
ядерной энергии:
)
конвекцией может быть охвачена большая часть звезды, поэтому здесь перемешивание
приводит к тому, что химический состав меняется у всей звезды в целом. У более
массивных звезд конвекция отсутствует вообще либо происходит в небольшой
центральной части, где выделяется энергия, и для них изменение химического состава
является функцией только лагранжевой координаты и пропорционально скорости выделения
ядерной энергии:
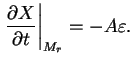
В дальнейшем будем рассматривать модели без конвекции. Итак, имеем четыре дифференциальных
уравнения для величин
![]() и
и ![]() с граничными условиями:
с граничными условиями:
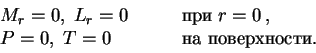
В центре можно варьировать два параметра ![]() и
и ![]() .
.
Если теперь мы будем интегрировать эти уравнениями с фиксированными начальными
параметрами, то не всегда ![]() и
и ![]() обратятся в нуль одновременно на поверхности
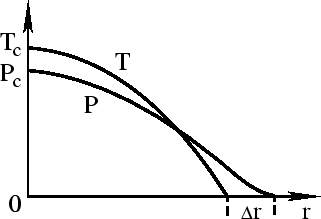
(рис. 31). Это условие (
обратятся в нуль одновременно на поверхности
(рис. 31). Это условие (
![]() ) накладывает дополнительное ограничение на
) накладывает дополнительное ограничение на
![]() и
и ![]() . Поэтому семейство решений будет однопараметрическим (по
. Поэтому семейство решений будет однопараметрическим (по ![]() или
или
![]() ). При данном
). При данном ![]() есть одно
есть одно ![]() , такое что
, такое что
![]() . Итак, при
учете этого условия
. Итак, при
учете этого условия
![]() . Если бы мы рассматривали только
механическое равновесие, то можно было бы варьировать два параметра (скажем
. Если бы мы рассматривали только
механическое равновесие, то можно было бы варьировать два параметра (скажем ![]() и
и
![]() ). Но еще необходимо, чтобы выделение энергии и ее отвод компенсировали друг
друга (условие теплового баланса). Это дополнительное условие ограничивает
количество решений: для данного
). Но еще необходимо, чтобы выделение энергии и ее отвод компенсировали друг
друга (условие теплового баланса). Это дополнительное условие ограничивает
количество решений: для данного ![]() есть единственная модель с одним значением
массы, следовательно, для данной массы есть определенное значение
есть единственная модель с одним значением
массы, следовательно, для данной массы есть определенное значение ![]() и определенная
светимость6.1.
и определенная
светимость6.1.
<< 5.6 Поиски солнечных нейтрино | Оглавление | 6.2 Соотношение масса-светимость >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |