<< 6.2 Соотношение масса-светимость | Оглавление | 6.4 Эволюция звезд главной ... >>
6.3 Тепловая устойчивость звезд
Раньше мы рассматривали вопросы механического равновесия звезд. Теперь нас будет интересовать их тепловая устойчивость, т. е. мы попытаемся понять, почему Солнце и другие звезды, обладая огромными запасами взрывоопасного вещества, весьма ``разумно'' расходует его на протяжении миллионов и даже миллиардов лет.
Тепловое равновесие вообще определяется равенством скоростей процессов энерговыделения и энергоотвода. Система устойчива в тепловом отношении в том случае, когда при небольшом возмущении температуры эти процессы меняются так, чтобы ликвидировать начальное возмущение.
Пусть в центре звезды ``горит'' водород и выделяющаяся энергия отводится теплопроводностью. Что произойдет при небольшом изменении температуры?
Из уравнения диффузии излучения получаем, что отвод тепла (светимость звезды) следующим образом зависит от физических величин:
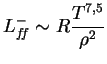
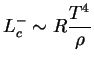
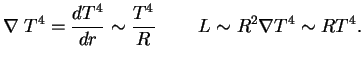
Как обстоит дело с подводом тепла ![]() ? Из полученных в предыдущем параграфе
соотношений имеем:
? Из полученных в предыдущем параграфе
соотношений имеем:
Почему в ![]() плотность
плотность ![]() входит в первой степени? Вероятность процесса на
атом пропорциональна
входит в первой степени? Вероятность процесса на
атом пропорциональна ![]() , на единицу объема
, на единицу объема
![]() . Следовательно, по
всей массе звезды
. Следовательно, по
всей массе звезды
![]() .
.
В CNO-цикле есть процессы типа
![]() , вероятность
которых не зависит от
, вероятность
которых не зависит от ![]() , но они быстры (см. 5.5),
а процессы типа столкновений
(в которые
, но они быстры (см. 5.5),
а процессы типа столкновений
(в которые ![]() входит) медленны. Именно последние и лимитируют выделение
энергии, т. е. они определяют скорость подвода тепла.
входит) медленны. Именно последние и лимитируют выделение
энергии, т. е. они определяют скорость подвода тепла.
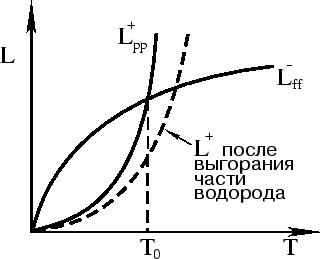
Итак, в равновесии ![]() при некотором фиксированном значении температуры (см.
рис. 32).
при некотором фиксированном значении температуры (см.
рис. 32).
Является это равновесие устойчивым? На первый взгляд кажется, что небольшое увеличение температуры приведет к возрастанию энерговыделения, что в свою очередь поднимает температуру дальше и ведет к взрыву звезды. При уменьшении температуры отвод энергии становиться больше, чем ее выделение, и, казалось бы, звезда должна остыть. Подобная ситуация возникает при неустойчивости горения обычных веществ на Земле.
Однако звезды устойчивы. Где ошибка в наших рассуждениях? Мы не учли факт, что звезда имеет отрицательную теплоемкость. В общем случае изменение температуры со временем определяется уравнением
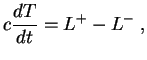
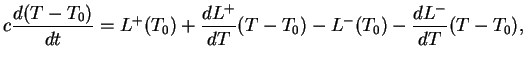
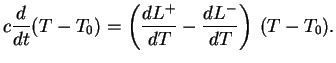
Для звезды полная энергия
Следует помнить, что эти рассуждения справедливы только в тех случаях, когда,
во-первых, при малых возмущениях звезда расширяется (или сжимается) как целое и,
во-вторых, тепловая энергия ![]() пропорциональна температуре
пропорциональна температуре ![]() , т. е. когда звезда
невырождена. Когда эти условия не выполняются, то может возникнуть неустойчивость.
, т. е. когда звезда
невырождена. Когда эти условия не выполняются, то может возникнуть неустойчивость.
Рассмотрим теперь, как изменяется со временем положение теплового равновесия по
мере выгорания водорода. Ясно, что с уменьшением общего количества водорода в центре
кривая ![]() будет со временем понижаться
(см. рис. 32).
Как видно, температура в
центре постепенно растет, увеличивается центральная плотность звезды, растет светимость.
Как показывают расчеты, радиус звезды изменяется в ту или другую сторону в
зависимости от наличия перемешивания. В отсутствии конвекции, когда звезда со
временем становится химически неоднородной, размеры ее увеличиваются, т. е. звезда
постепенно ``разбухает''. Однако до тех пор, пока водород не выгорит в центре, все
эти изменения столь медленны и незначительны, что в первом приближении можно считать
звезду почти неизменной. Поскольку калорийность водорода велика, звезда долго
находится в состоянии горения водорода в ее центральных частях. В этом состоянии
проходит большая часть ее жизни, именно поэтому преобладающее большинство звезд
сконцентрировано на главной последовательности диаграммы Гершпрунга-Рессела.
Приведем время жизни в годах на главной последовательности для нескольких
значений масс звезд:
будет со временем понижаться
(см. рис. 32).
Как видно, температура в
центре постепенно растет, увеличивается центральная плотность звезды, растет светимость.
Как показывают расчеты, радиус звезды изменяется в ту или другую сторону в
зависимости от наличия перемешивания. В отсутствии конвекции, когда звезда со
временем становится химически неоднородной, размеры ее увеличиваются, т. е. звезда
постепенно ``разбухает''. Однако до тех пор, пока водород не выгорит в центре, все
эти изменения столь медленны и незначительны, что в первом приближении можно считать
звезду почти неизменной. Поскольку калорийность водорода велика, звезда долго
находится в состоянии горения водорода в ее центральных частях. В этом состоянии
проходит большая часть ее жизни, именно поэтому преобладающее большинство звезд
сконцентрировано на главной последовательности диаграммы Гершпрунга-Рессела.
Приведем время жизни в годах на главной последовательности для нескольких
значений масс звезд: ![]() ,
, ![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
, ![]() .
.
<< 6.2 Соотношение масса-светимость | Оглавление | 6.4 Эволюция звезд главной ... >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |
![$\displaystyle \cdot\exp\left[\left({dL^+\over{dT}}-{dL^-\over{dT}}\right) {t \over c} \right]\,.$](https://images.astronet.ru/pubd/2008/02/15/0001226214/img1311.gif)