<< 6.1 Уравнения звездой структуры | Оглавление | 6.3 Тепловая устойчивость звезд >>
6.2 Соотношение масса-светимость
Вид уравнений позволяет найти ряд соотношений для интегральных характеристик звезд
(масса, светимость, радиус), не решая численно систему. Это можно сделать в том
случае, когда непрозрачность ![]() и энерговыделение
и энерговыделение
![]() степенным образом
зависят от плотности и температуры. На самом деле эти зависимости различны для
различных слоев, и, более того, в некоторых случаях вообще нельзя применять степенную
аппроксимацию. Тем не менее для широкого класса ``гладких'' моделей получающиеся
соотношения подтверждаются прямым численным расчетом.
степенным образом
зависят от плотности и температуры. На самом деле эти зависимости различны для
различных слоев, и, более того, в некоторых случаях вообще нельзя применять степенную
аппроксимацию. Тем не менее для широкого класса ``гладких'' моделей получающиеся
соотношения подтверждаются прямым численным расчетом.
В выражениях для непрозрачности будем пользоваться при низких температурах законом Крамерса:
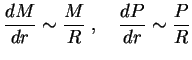 и т. д.
и т. д.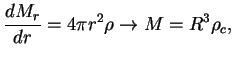
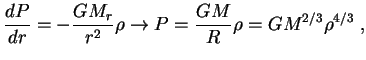
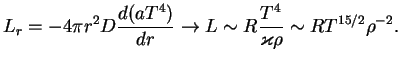
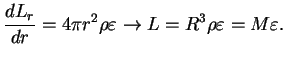
В случае томсоновской непрозрачности (высокие температуры)
<< 6.1 Уравнения звездой структуры | Оглавление | 6.3 Тепловая устойчивость звезд >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |
Астрометрия
-
Астрономические инструменты
-
Астрономическое образование
-
Астрофизика
-
История астрономии
-
Космонавтика, исследование космоса
-
Любительская астрономия
-
Планеты и Солнечная система
-
Солнце