Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Физические основы строения и эволюции звезд
<< 5.4 Слабое взаимодействие | Оглавление | 5.6 Поиски солнечных нейтрино >>

5.5 Ядерные реакции в звездах

Эйнштейновское соотношение между массой и энергией вещества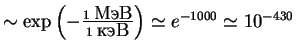 $ E=mc^2$ показывает, что ядерные реакции могут быть источником энергии звезд. В самом деле, масса четырех протонов больше массы ядра гелия: $ 4m_p>m_{\rm He}$, и образование последнего в результате слияния четырех протонов должно происходить с огромным выделением энергии, равным разности массы -- дефекту масс $ \Delta E=(4m_p-m_{\rm He})c^2$. Однако долгое время до появления квантовой механики казалось, что температура вещества в центре звезды, $ T\sim GM/({\cal R}R)\sim 1\;$кэВ, слишком низка. Для преодоления кулоновского отталкивания при столкновении двух протонов необходима энергия порядка 1 МэВ. При максвелловском распределении с температурой $ \sim$1 кэВ энергией в 1 МэВ обладает доля частиц $ \sim\exp\left(-{1\;\mbox{МэВ}\over{1\; \mbox{кэВ}}}\right)\simeq e^{-1000}\simeq 10^{-430}$ (отметим, что в Солнце всего $ 10^{57}$ частиц, т.е. классическая вероятность взаимодействия двух протонов ничтожна). Тем не менее один из основателей теории внутреннего строения звезд А. Эддингтон, первый указавший на возможность реакции $ \mathrm{H}\to{}^{4}{\mathrm{He}}$, не сдавался, когда ему указывали на малую вероятность из-за недостаточно высокой температуры, и говорил: ``Поищите-ка место погорячее!''.

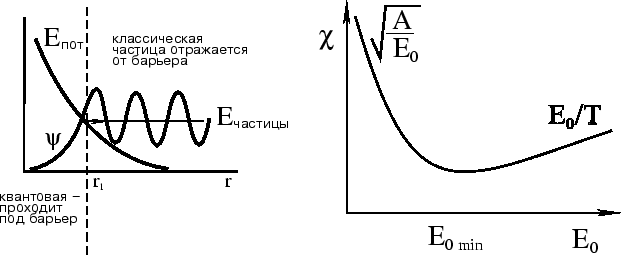
С развитием квантовой механики стало ясно, что Эддингтон прав! Вероятность ядерных реакций увеличивается благодаря подбарьерному переходу (туннельный эффект).

Оценим скорость ядерных реакций с учетом законов квантовой механики. Напомним известное соотношение Де Бройля, связывающее длину волны $ \lambda$ (волновое число $ k=2\pi/ \lambda$) и импульс частицы $ p$: $ k=p/\hbar$. Движению с импульсом $ p$ соответствует волновая функция $ e^{ikx}\to e^{{ipx\over \hbar}}$ или $ e^{{i\over\hbar}\int pdx}$, если $ p$ является функцией координат. Для частиц с массой покоя $ m$ импульс $ p$ найдем из закона сохранения энергии

$\displaystyle p^2/(2m)=E_{\mbox{кин}}=E_{\mbox{полн}}-U=E_0-U\;. $

Отсюда

$\displaystyle p=\sqrt{2m(E_0-U)}\;. $

Для двух частиц с зарядами $ Z_1,Z_2$ энергия отталкивания

$\displaystyle U=Z_1Z_2e^2/r\;. $

В классической механике частица с энергией $ E$ при достижении точки $ r_1$, где $ p=0$, т.е. $ r_1=Z_1Z_2/E$, поворачивает и движется в обратную сторону. В квантовой теории при $ r<r_1\;p=i\sqrt{2m(U-E_0)}$, и в волновую функцию частицы, идущей с бесконечности, войдет множитель

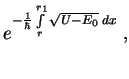
$\displaystyle e^{-{1\over\hbar}\int\limits_r^{r_1}\sqrt{U-E_0}\;dx}\;, $

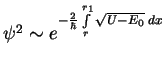т.е. существует конечная вероятность $ \psi^2\sim e^{-{2\over\hbar}\int\limits_r^{r_1} \sqrt{U-E_0}\;dx}$ прохождения частицы в область $ r<r_1$ (см. рис. 29).

Рассмотрим интеграл

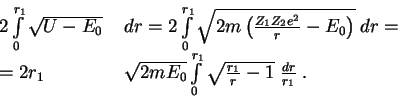
\begin{displaymath} \begin{array}{ll} 2\int\limits_0^{r_1}\sqrt{U-E_0}\;&dr=2\in... ...{r_1}\sqrt{{r_1\over {r}}-1}\;{dr\over{r_1}}\;. \cr \end{array}\end{displaymath}

Пусть

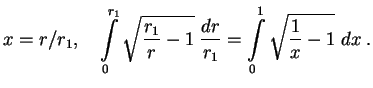
$\displaystyle x=r/r_1,\quad \int\limits_0^{r_1}\sqrt{{r_1\over {r}}-1}\;{dr\over{r_1}}=\int\limits_0^1\sqrt{{1\over{x}} -1}\;dx\;. $

При $ x\to 0$ подынтегральное выражение $ \to \infty$, однако интеграл сходится:

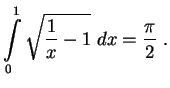
$\displaystyle \int\limits_0^1\sqrt{{1\over{x}}-1}\;dx={\pi \over 2}\;. $

Отметим, что сходимость интеграла позволяет нам вести интегрирование от нуля, а не от радиуса ядерного взаимодействия $ r_2$, который составляет $ \sim 10^{-3}r_1$. Ясно, что такое приближение (замена $ r_2\to 0$) даст лишь небольшой поправочный множитель.

При точном вычислении вероятности перед экспонентой есть еще степенные множители, которые мы не учитываем. Для нас сейчас важна только экспонента.

Итак, $ \psi^2(0)=e^{-\varphi}$, где

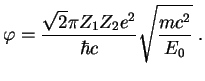
$\displaystyle \varphi={\sqrt{2}\pi Z_1Z_2e^2\over{\hbar c}}\sqrt{{mc^2\over{E_0}}}\;. $

Рис. 29.Рис. 30.

Выше предполагалось, что одно из ядер покоится ( $ m_2=\infty$). На самом деле при расчете в системе центра масс вместо $ m$ следует, как обычно, подставить приведенную массу $ \mu={m_1m_2\over{m_1+m_2}}$. Тогда

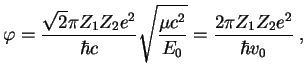
$\displaystyle \varphi={\sqrt{2}\pi Z_1Z_2e^2\over{\hbar c}}\sqrt{{\mu c^2\over{E_0}}}={2\pi Z_1Z_2e^2 \over{\hbar v_0}}\;, $

где $ v_0$ -- относительная скорость частиц на бесконечности. В таком виде видна безразмерность $ \varphi$ (аналогично $ e^2/(\hbar c)$).

Мы получили вероятность подбарьерного сближения частиц с данной энергией $ E_0$: $ \sim e^{-\sqrt{{A\over{E_0}}}}$, где $ A={2\pi^2Z_1^2Z_2^2e^4\over{\hbar^2}}\cdot {A_1A_2\over{A_1+A_2}}m_u\;$($ A_1$, $ A_2$ -- атомные массы ядер). В тепловом равновесии (при температуре $ T$) количество частиц с энергией $ E_0$ пропорционально $ e^{-{E_0\over{T}}}$ и полная вероятность

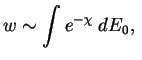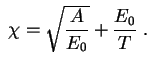
$\displaystyle w\sim\int e^{-\chi}\;dE_0,\;$где$\displaystyle \;\chi=\sqrt{{A\over{E_0}}}+{E_0\over{T}}\;. $

Функция $ \chi(E_0)$ имеет минимум при некотором значении $ E_{0\,\min}$ (см. рис. 30). Очевидно, что область минимума даст главный вклад в интеграл, так как $ e^{-\chi}$ в этой точке имеет острый максимум. Вычисление таких интегралов проводится методом перевала. Сначала находим экстремум:

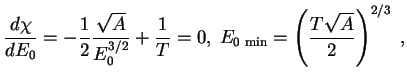
$\displaystyle {d\chi\over{dE_0}}=-{1\over2}{\sqrt{A}\over{E_0^{3/2}}}+{1\over T}=0,\;E_{0\,\min}=\left( {T\sqrt{A}\over 2}\right)^{2/3}\;, $

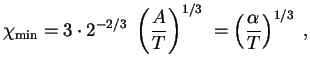
$\displaystyle \chi_{\min}=3\cdot 2^{-2/3}\;\left({A\over T}\right)^ {1/3}\;=\left({\alpha\over T}\right)^{1/3}\;, $

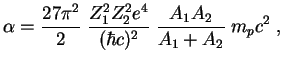
$\displaystyle \alpha={27\pi^2\over2}\;{Z_1^2Z_2^2e^4 \over{(\hbar c)^2}}\;{A_1A_2\over{A_1+A_2}}\;m_pc^2\;, $

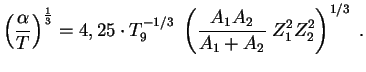
$\displaystyle \left({\alpha\over T}\right)^ {1\over3}=4,25\cdot T_9^{-1/3}\;\left({A_1A_2\over{A_1+A_2}}\;Z_1^2Z_2^2\right)^{1/3}\;. $

Здесь $ T_9=T/10^9$ K -- температура в млрд. градусов. Теперь можно разложить $ \chi(E_0)$ в ряд Тейлора в окрестности точки $ E_{0\,\min}$:

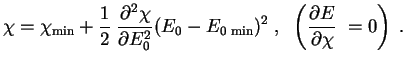
$\displaystyle \chi=\chi_{\min}+{1\over2}\;{\partial^2\chi\over\partial E_0^2}(E_0-E_{0\,\min})^2 \;,\;\;\left({\partial E\over\partial\chi}\;=0\right)\;. $

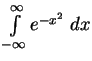Итак, $ w =e^{-\chi_{\min}}$ с некоторым множителем, получающимся от интегрирования второго члена, которое сводится к интегралу вида $ \int\limits_{-\infty}^{\infty}e^{-x^2}\;dx$ (проведите это интегрирование!). Так мы нашли только вероятность сближения ядер. Полная вероятность реакции получится после умножения на вероятность соответствующего взаимодействия.

Перейдем к конкретным реакциям.

$\displaystyle 1)\quad p+p=\mathrm{D}+e^++\nu. $

Выделение энергии в этой реакции $ Q=1,442\;$МэВ, в том числе $ \sim0,25\;$МэВ уносят нейтрино.

Число ядер дейтерия D, рождающихся в 1 см$ ^3$ на 1 с, равно

$\displaystyle {d[\mathrm{D}]\over{dt}}={1\over2}\;{n^2_p\over{6\cdot 10^{23}}}\... ...{-15}T^{-2/3} _9e^{-3,38/T_9^{1/3}}\left[\mbox{с}^{-1}\,\mbox{см}^{-3}\right]. $

Вводя весовые доли для химических элементов

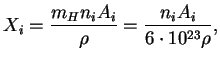
$\displaystyle X_i={m_Hn_iA_i\over{\rho}}={n_iA_i\over{6\cdot 10^{23}\rho}}, $

получим

$\displaystyle {dX_{\rm D}\over{dt}}=4,2\cdot 10^{-15}\rho X_{\rm H}^2T^{-2/3}_9e^{-3,38/T_9^{1/3}} \left[\mbox{с}^{-1}\right]. $

$\displaystyle 2)\quad \mathrm{D}+p\to {}^{3}{\mathrm{He}}+\gamma,\quad Q=5,494\;$МэВ$\displaystyle , $

$\displaystyle {dX_{{}^{3}\mathrm{He}}\over{dt}}=3,98\cdot 10^3\cdot X_{\rm H}X_{\rm D}\rho T^{-2/3}_9e^{-3,72/T_9^{1/3}}\left[\mbox{с}^{-1}\right]. $

Укажем на большую разницу (10$ ^{18}$ раз) в отношении коэффициентов в первой и во второй реакции. Это объясняется тем, что первая реакция идет со слабым взаимодействием на лету, а во второй все определяется электромагнитным взаимодействием. Отметим также, что вторая реакция в условиях земных морей и океанов ``зарезается'' экспонентой, несмотря на большой множитель, стоящий перед ней.

$\displaystyle 3)\quad {}^{3}{\mathrm{He}}+{}^{3}{\mathrm{He}}\to {}^{4}{\mathrm{He}}+2p,\quad Q=12,86\;$МэВ$\displaystyle . $

Скорость реакции:

$\displaystyle {dX_{{}^4\mathrm{He}}\over{dt}}=1,3\cdot 10^{10}\rho X_{{}^3\mathrm{He}}^2T^{-2/3}_9 e^{-{12,28\over{T_9^{1/3}}}}\left[\mbox{c}^{-1}\right]. $

Здесь множитель еще больше, так как реакция идет по сильному взаимодействию.

Итак, мы видим, что благодаря цепочке реакций 1), 2), 3) возможно превращение четырех ядер водорода в ядро гелия с выделением энергии $ (m_{\rm He}^4-4m_{\rm H})c^2$. Эта цепочка реакций может идти при достаточно высокой температуре в абсолютно чистом водороде и называется протон-протонным (или $ pp$-) циклом. Возможны и другие цепочки протон-протонного цикла.

Расчет показывает, что при низких температура $ (T<2\cdot 10^7$ K реакции идут в основном по двум следующим схемам:

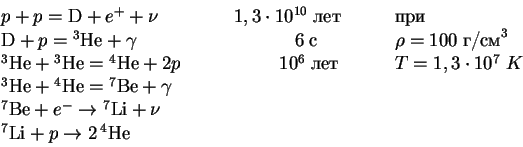
\begin{displaymath} \begin{array}{lcl} %% здесь !!!!!!!!!!! p+p=\mathrm{D}+e^++\... ... {}^{7}{\mathrm{Li}}+p\to 2\, {}^{4}{\mathrm{He}} \end{array}\end{displaymath}

Справа указано характерное время реакций (как оно вычислено?).

Ясно, что без участия слабого взаимодействия водород в He не превратить, так как из протонов надо получить нейтроны. свободный протон в нейтрон не превращается -- это возможно только в поле другого протона, который его подхватывает. На одно ядро $ {}^{4}{\mathrm{He}}$ должно пройти две реакции $ p+p\to \mathrm{D}+e^++\nu$. На каждую реакцию $ p+p$ во всем $ pp$-цикле выделяется 13,086 МэВ энергии.

Вторая цепочка интересна потому, что дает побочные продукты:

$\displaystyle {}^{7}{\mathrm{Be}}+p\to {}^{8}{\mathrm{B}}+\gamma, $

$\displaystyle {}^{8}{\mathrm{B}}\to {}^{8}{\mathrm{Be}}+e^++\nu. $

Последний распад замечателен тем, что он дает нейтрино высокой энергией, в среднем $ E=8$-9 МэВ, которые можно детектировать на Земле (см. ниже).

Очевидно, что скорость выделения энергии в $ pp$-цикле равна скорости, с которой идет первая реакция:

$\displaystyle p+p=\mathrm{D}+e^++\nu. $

Дейтерий тут же вступает в реакцию с протоном. Поэтому он не накапливается и стационарная концентрация

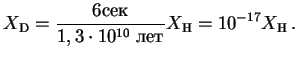
$\displaystyle X_{\rm D}={6\mbox{сек}\over{1,3\cdot10^{10}\;\mbox{лет}}}X_{\rm H}=10^{-17}X_{\rm H}\,. $

Выпишем полную скорость энерговыделения в $ pp$-цикле:

$\displaystyle \varepsilon_{pp}=\rho X_{\rm H}^2\;\varepsilon_0(T/T_0)^n\;[$эрг/(г$\displaystyle \cdot$c)$\displaystyle ] $

$ T_0/10^6$ $ \varepsilon_0$ $ n$
1 $ 4\cdot 10^{-9}$ 10,6
5 $ 1,8\cdot10^{-3}$ 5,95
10 $ 6,8\cdot10^{-2}$ 4,60
15 0,377 3,95
20 1,09 3,64
30 4,01 3,03

При температурах более высоких, чем солнечные (в более массивных звездах), идет CNO-цикл (он возможен только в присутствии катализатора углерода)

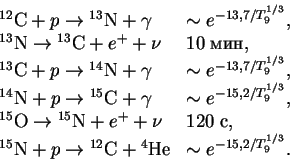
\begin{displaymath} \begin{array}{ll} {}^{12}{\mathrm{C}}+p\to{}^{13}{\mathrm{N}... ...{C}}+{}^{4}{\mathrm{He}}& \sim e^{-15,2/T_9^{1/3}}. \end{array}\end{displaymath}

Обратите внимание на то, что в последней реакции снова образуется ядро $ {}^{12}{\mathrm{C}}$, с которого начиналась первая реакция. Отметим, что в отличии от $ pp$-цикла здесь слабое взаимодействие идет не на лету, т.е. слабое взаимодействие и подбарьерный переход разделены. Поскольку в CNO-цикле участвуют ядра с более высоким зарядами, он идет при более высокой температуре, причем зависимость от температуры более крутая, чем в $ pp$-цикле. Энерговыделение во всем CNO-цикле в расчете на одну реакцию $ {}^{14}{\mathrm{N}}+p$ (самую медленную) равно 24,97 МэВ. Выпишем полную скорость энерговыделения в CNO-цикле:

$\displaystyle \varepsilon=\varepsilon_0\rho X_{\rm H}X_{\rm CNO}(T/T_0)^n\;[$эрг/г c$\displaystyle ] $

$ T_0/10^6$ $ \varepsilon_0$ $ n$
6 $ 9\cdot10^{-10}$ 27,3
10 $ 3,4\cdot10{-4}$ 22,9
15 1,94 19,9
20 $ 4,5\cdot10^2$ 18,0
30 $ 4,1\cdot10^5$ 15,6
50 $ 6,2\cdot10^8$ 13,6
100 $ 1,9\cdot10{12}$ 10,2

З а д а ч и.

1. Подсчитать, при какой температуре D выгорает за $ 10^6$ лет. То же для $ {}^{3}{\mathrm{He}}$.

2. Найти условия, при которых энерговыделение

$\displaystyle \varepsilon_{\rm CNO}=\varepsilon_{pp}. $

3. Вычислить скорость реакций:
а). $ \displaystyle{{}^{3}{\mathrm{He}}+p= {}^{4}{\mathrm{He}}+e^++\nu}$
(в этой реакции выделяются высокоэнергичные нейтрино),
б). $ \displaystyle{{}^{3}{\mathrm{He}}+e^-\to {}^{}{\mathrm{T}}+\nu}$
(указание: использовать экспериментальные данные по распаду $ \mathrm{T}\to{}^{3}{\mathrm{He}}+e^-+\widetilde\nu$: энергия (не включая $ m_ec^2$) 0,0186 МэВ, время жизни 12,26 лет. Рассмотреть равновесие с невырожденными электронами при высокой температуре),
в). $ \displaystyle{\mathrm{T}+p\to {}^{4}{\mathrm{He}}+\gamma\,}$


<< 5.4 Слабое взаимодействие | Оглавление | 5.6 Поиски солнечных нейтрино >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 119]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования