Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Физические основы строения и эволюции звезд
<< 5.3 Учет электромагнитного ... | Оглавление | 5.5 Ядерные реакции в ... >>

5.4 Слабое взаимодействие

Типичный пример слабого взаимодействия -- превращение нейтрона в протон с испусканием электрона и антинейтрино $ \widetilde \nu$:

$\displaystyle n\to p+e^-+\widetilde \nu\;. $

Взаимодействие называется слабым из-за малой скорости распада. Время жизни свободного нейтрона порядка 10 мин. Выше мы рассматривали реакции с характерными временами $ 10^{-22}$ с для чисто ядерного взаимодействия и $ 10^{-16}$ с участием электромагнитного взаимодействия, т.е. с испусканием $ \gamma$-квантов.

Подчеркнем, что при слабых взаимодействиях, как и при электромагнитных, реакции идут с рождением новых частиц, т.е. число частиц не сохраняется. Ни в коем случае нельзя считать, что $ e^-$ и $ \widetilde \nu$ ``сидят'' в нейтроне, что нейтрон есть связанная система из протона и электрона. Нейтрон так же элементарен, как и протон5.2. Частицы действительно рождаются. Здесь можно провести аналогию со звуком: коснемся струны -- рождаются фононы.

В реакциях такого рода можно переносить частицу справа налево и слева направо (с обязательной заменой частицы на античастицу):

$\displaystyle e^++n\rightleftarrows p+\widetilde \nu\,, $

$\displaystyle \nu+n\rightleftarrows p+e^-\,, $

$\displaystyle p\rightleftarrows n+e^++\nu\,. $

Чем отличается антинейтрино $ \widetilde \nu$ от нейтрино $ \nu$? Для $ \nu$ и $ \widetilde \nu$ масса покоя $ m=0$, заряд $ e=0$ и, казалось бы, различий между ними нет. Отличаются они по типу реакций, в которых участвуют. Например, вблизи реактора экспериментально наблюдалась реакция $ \widetilde \nu+p\to n+e^+$ и нет реакции $ \nu+n\to p+e^-$, так как реактор дает только антинейтрино. Если бы эти частицы были тождественны (как фотон и антифотон), то ничто не мешало бы получить реакцию $ \nu+n\to p+e^-$. Так же по типу реакций было открыто, что нейтрино бывают двух сортов: нейтрино электронное $ \nu_e$ и нейтрино мюонное $ \nu_\mu$. Последние участвуют в реакциях типа

$\displaystyle p+\mu^-\to n+\nu_\mu\;, $

где $ \mu^-$ -- мю-мезон5.3.

Следующий важный момент слабых взаимодействий: как понимать реакцию $ p\to n+e^+ +\nu$? Ведь протон стабилен. Мы писали реакции только с учетом законов сохранения зарядов. Но нужно также удовлетворить еще и закону сохранения энергии. Однако сохранение заряда -- абсолютно, а на энергию системы можно воздействовать извне.

Масса нейтрона равна

$\displaystyle m_n=M_{\rm H}+0,78 \;$МэВ$\displaystyle =m_p+m_e+0,78 \;$МэВ$\displaystyle \;, $

Рис. 28.

где $ M_{\rm H}$ -- масса атома водорода (ясно, что $ M_{\rm H}=m_p+m_e$, поскольку энергией связи электрона в атоме водорода $ \sim$13,6 эВ можно пренебречь). Поэтому реакция $ p\to n+e^+ +\nu$ в свободном состоянии идти не может -- не хватает энергии. Но возьмем связанные $ n$ и $ p$ в системах: $ {}^{13}{\mathrm{C}}={}^{12}{\mathrm{C}}+n$ и $ {}^{13}{\mathrm{N}}={}^{12}{\mathrm{C}}+p$ (см. рис. 28). По ядерным силам $ {}^{12}{\mathrm{C}}$ одинаково взаимодействует как с $ p$, так и с $ n$, но кулоновское отталкивание уменьшает энергию связи протона. Связанный в ядре $ {}^{12}{\mathrm{C}}$ протон $ p_{bound}$ оказался ``тяжелее'' связанного нейтрона, поэтому может идти реакция $ {}^{13}{\mathrm{N}}\to {}^{13}{\mathrm{C}}+e^+ +\nu$, т.е.

$\displaystyle p_{bound}\to n_{bound} +e^+ +\nu\;. $

Стабильность протона и нестабильность нейтрона в некотором смысле условны, так как в связанном состоянии стабильным может оказаться нейтрон, а не протон.

Пойдет ли реакция $ p+e^-\to n+\nu$? Ведь $ m_n>m_p+m_e$ и нейтрон должен распадаться. В силу этого неравенства реакция не пойдет ни в атоме водорода, ни в плазме малой плотности и температуры: $ \rho <10^4\;$$ \mbox {г/см}^3$, $ T<10^9$ K. Однако реакция пойдет либо в случае, когда нейтрон сильно связан, либо когда электрон имеет большую энергию. Типичный пример: $ {}^{7}{\mathrm{Be}}+e^-={}^{7}{\mathrm{Li}}+\nu$, нейтрон в Li крепко связан. Большая энергия электронов может быть обусловлена либо высокой температурой, либо их вырождением при большой плотности. Например, в вырожденном газе при высоком давлении реакция $ p+e^-\to n+\nu$ идет при ферми-энергии электронов $ E_f>0,78\;$МэВ. В этом случае эта реакция носит название реакции нейтронизации вещества -- главный момент в теории пульсаров и нейтронных звезд.

Такие реакции могли бы идти и в горячей плазме, когда энергия электронов достаточно высока: но там есть более эффективные реакции с испусканием $ \gamma$-квантов, которые быстро отнимают энергию у электронов. Поэтому в разреженной плазме нейтронизация пренебрежима из-за слабости взаимодействия. К тому же нейтрон распадается обратно на протон и электрон (с образованием $ \widetilde \nu$). Интересно заметить, что в той же горячей плазме, когда выход излучения из системы затруднен (большая непрозрачность вещества), процессы слабого взаимодействия с образованием нейтрона и их распадом могут эффективно отводить энергию через испускание $ \nu$ и $ \widetilde \nu$ (так называемые урка-процессы, см. раздел 7.4).

Слабые взаимодействия называются четырехфермионными, так как в реакциях участвуют 4 ферми-частицы со спином $ s=1/2$.

Вероятность взаимопревращения частиц за счет слабого взаимодействия по аналогии с теорией электромагнитного излучения записывается в виде

$\displaystyle W={2\pi \over \hbar}\; \vert H'\vert^2{dN \over dE}\;\left[c^{-1}\right]\;, $

где $ dN/dE$ -- число конечных состояний на единичный интервал энергии, а $ H'$ -- матричный элемент гамильтониана взаимодействия, определяющий, таким образом, комплексную амплитуду вероятности процесса. В простейшей теории слабых взаимодействий полагают, что

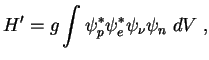
$\displaystyle H'=g\int\psi^*_p \psi^*_e \psi_{\nu}\psi_n \;dV\;, $

где $ g$ -- постоянная слабого взаимодействия, а $ \psi_n$, $ \psi_p$, $ \psi_e$, $ \psi_{\nu}$ -- волновые функции частиц. В это выражение необходимо подставлять $ \psi$ или $ \psi^*$ (сопряженную волновую функцию) соответственно тому, уничтожается или рождается частица. Выражение $ H'$ написано для распада нейтрона $ n\to p+e^-+\widetilde \nu_e$, поэтому мы пишем $ \psi^*_p,\;\psi_e^*$. Волновая функция нейтрино $ \psi_{\nu}$ пишется без звездочки, так как рождение антинейтрино $ \widetilde \nu_e$ эквивалентно уничтожению $ \nu_e$. Важный момент -- размерность $ g$. Так как размерность $ [H]=$эрг, а $ \int\psi^2dV=1$, т.е. $ [\psi]=$cм$ ^{-3/2}$, то $ [g]=$эрг$ \cdot$см$ ^3$. Заметим, что константа электромагнитного взаимодействия $ e^2/hc=1/137$ безразмерна. В системе CGS численно $ g=1,4\cdot10^{-49}\;$эрг$ \cdot$см$ ^3$. Зная $ g$ (из опыта), можно определить вероятность распада $ n\to p+e^-+\widetilde \nu$. Пусть энергии выделилось много, тогда электрон $ e^-$ -- релятивистский, и $ m_e$ не должна входить в ответ. Вероятность $ W$ пропорциональна квадрату матричного элемента, т.е. пропорциональна $ g^2$. Необходимо подобрать такую комбинацию степеней $ E$, $ \hbar$ и $ c$, чтобы получить размерность $ [W]=c^{-1}$:

$\displaystyle W\sim\;g^2E^n\;\hbar^m\;c^p\;, $

т.е.

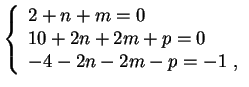
$\displaystyle \left\{\begin{array}{l} 2+n+m=0 \\ 10+2n+2m+p=0 \\ -4-2n-2m-p=-1\;, \end{array}\right. $

откуда $ n=5,\;m=-7,\;p=-6$.

Точная формула имеет вид

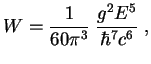
$\displaystyle W={1 \over {60\pi ^3}}\;{g^2E^5\over {\hbar ^7 c^6}}\;, $

где коэффициент $ 1/60\pi^3$ получен из конкретного расчета.

З а д а ч а 1. Рассмотрим реакцию

$\displaystyle e^-+p\to n+\nu\;. $

Пусть энергия электронов $ 5\,$МэВ$ <E_e<100\,$МэВ. Тогда протон и нейтрон можно считать покоящимися. Построить по размерности выражение для $ \sigma[$$ \mbox {см}^2]$:

$\displaystyle \sigma (E) \sim g^2E^n\hbar ^mc^p\;. $

З а д а ч а 2. Найти вероятность нейтронизации в вырожденном газе релятивистских электронов

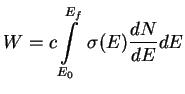
$\displaystyle W=c\int\limits^{E_f}_{E_0}\;\sigma (E){dN\over {dE}}dE $

($ E_0$ -- пороговая энергия нейтронизации).


<< 5.3 Учет электромагнитного ... | Оглавление | 5.5 Ядерные реакции в ... >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 120]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования