Астронет > 5.3 Учет электромагнитного взаимодействия частиц

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Физические основы строения и эволюции звезд

<< 5.2 Простейшие примеры | Оглавление | 5.4 Слабое взаимодействие >>

5.3 Учет электромагнитного взаимодействия частиц

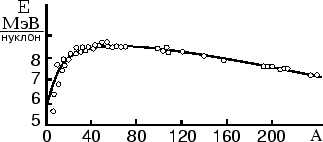
Электромагнитное взаимодействие играет роль поправки к ядерным силам -- мы видели это на примере ${}^{3}{\mathrm{He}}$ и ${}^{3}{\mathrm{T}}$ . Другой более сильный пример: ядро ${}^{6}{\mathrm{He}}$ -- связано, но с заменой двух нейтронов на два протона, не существует из-за кулоновского отталкивания. С учетом принципа Паули наиболее компактно можно уложить ядро с равным числом протонов и нейтронов, но из-за кулоновского отталкивания выгоднее брать несколько больше нейтронов. Например, $\strut_{92}^{238}$ U состоит из 146 нейтронов и 92 протонов, т.е. нейтронов в 1,5 раза больше. По этой же причине тяжелые ядра неустойчивы относительно деления.

Без кулоновского отталкивания две ``ядерные капли'' стремились бы слиться. Объемные энергии при этом просто складываются, а поверхностная -- уменьшается, так как поверхность большой капли меньше суммы поверхностей двух малых. Однако, вследствие того что кулоновские силы спадают по степенному закону, а ядерные -- по экспоненциальному, в крупных каплях (ядра с большим Z) далекие протоны уже не притягиваются друг к другу за счет ядерных сил, а только отталкиваются за счет кулоновских. Таким образом, кулоновская энергия не очень существенна в легких ядрах и важна в тяжелых, вследствие чего ядра с промежуточными значениями Z (Fe) наиболее прочно связаны (см. рис. 27).

Количественные поправки к энергии -- это одна сторона дела. Другой важный аспект учета электромагнитных взаимодействий -- это процессы рождения и поглощения фотонов:

$\displaystyle p+n\to {}^{2}{\mathrm{D}}+\gamma\;,$

$\displaystyle {}^{2}{\mathrm{D}}+p\to {}^{3}{\mathrm{He}}+\gamma\;.$

Реакция ${}^{2}{\mathrm{D}}+{}^{2}{\mathrm{D}}\to {}^{3}{\mathrm{T}}+p$ и подобные ей напоминают игру в кубики -- они сводятся просто к перегруппировке нуклонов. Здесь же происходит нечто новое -- рождение частиц (фотона не было, потом он родился). Из-за закона сохранения энергии реакция $p+n\to {}^{2}{\mathrm{D}}+\gamma$ не может идти без испускания фотона. Притяжение протона к нейтрону всегда есть, но если нуклоны сближаются и не рождают никакой частицы, то энергия сохраняется и они обязаны разлететься.

Теперь в сечение взаимодействия $p+n={}^{}{\mathrm{D}}+\gamma$ войдет вероятность рождения фотонов, т.е. появляется множитель $e^2/\hbar c=1/137$ . Рассмотрим процесс рождения фотонов на примере классического осциллятора. Для колеблющегося заряда энергия, выделяющаяся в единицу времени,

$\displaystyle Q\;\left[{\mbox{эрг}\over \mbox{с}}\right]\simeq{e^2\over c^3}\, \left({d^2x\over dt^2}\right)^2={e^2r^2\,\omega^4 \over c^3}\;.$

Время излучения одного кванта $\hbar\omega$

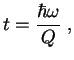
$\displaystyle t={\hbar\omega\over Q}\;,$

а вероятность этого процесса $W\sim 1/t$ , таким образом, равна

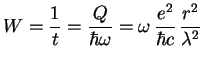
$\displaystyle W={1\over t}={Q\over \hbar\omega}=\omega\,{e^2\over \hbar c}\,{r^2\over \lambda^2}$

(здесь $\lambda=c/\omega$ ).

По порядку величины это выражение годится для любой системы и вероятность ядерных превращений с учетом электромагнитного взаимодействия

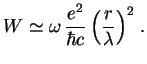
$\displaystyle W\simeq\omega\,{e^2\over \hbar c}\,{\left({r\over \lambda}\right)}^2\;.$

Для простой перегруппировки вероятность $W\sim 1/t\sim\omega$ . Теперь входят безразмерные величины $e^2/\hbar c$ -- сила взаимодействия и ${(r/\lambda)}^2$ -- отношение площади ``антенны'' к квадрату длины волны. Это верно при дипольных колебаниях. Если колебания имеют другую мультипольность, то входят более высокие степени $( r/\lambda)$ .

З а д а ч а. Известно сечение реакции $n+p\to D+\gamma$ ,

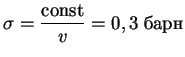
$\displaystyle \sigma={\mbox{const}\over v}=0,3\;\mbox{барн}$

при $v=2,7\cdot 10^5$ см/с (такая скорость соответствует скорости нейтронов при комнатной температуре). При высокой температуре, когда есть фотоны с энергией больше 2,2 МэВ, очевидно, будет происходить и обратный процесс фотодиссоциации дейтерия, и изменение концентрации дейтерия со временем описывается уравнением

$\displaystyle {d[\mathrm{D}]\over dt}=\sigma v\,[n]\,[p]-f\,(T)\,[\mathrm{D}]\;,$

здесь $[\mathrm{D}]$ -- концентрация D,

-- некоторая функция. В термодинамическом равновесии $\frac{d[\mathrm{D}]}{dt}=0$ и

$\displaystyle {[n]\,[p]\over [\mathrm{D}]}=F(T)\,\exp(-2,2\,$ МэВ $\displaystyle /kT)\;.$

Найти функции

и сечение фотодиссоциации дейтерия в зависимости от температуры.

(У к а з а н и е: пренебречь единицей в формуле Планка, т.е. считать ${(e^ x-1)}^{-1}\simeq e^{-x}$ ).

<< 5.2 Простейшие примеры | Оглавление | 5.4 Слабое взаимодействие >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы

См. также:

Переработка вещества в Кассиопее А

NGC 7789: Роза Каролины

Планетарная туманность NGC 2818 от Хаббла

Научная конференция "Наблюдаемые проявления эволюции звезд" в САО РАН

Планетарные туманности

Прошлые и будущие звёзды Андромеды

Туманность Ожерелье

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце