Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Физические основы строения и эволюции звезд
<< 7.3 Два типа энергетических ... | Оглавление | 8. Введение в OTO >>

7.4 Роль нейтрино в эволюции звезд

Выше мы уже отмечали качественное отличие процессов с рождением нейтрино от других механизмов потерь энергии. Рождаясь нейтрино практически беспрепятственно уходят из звезды и навсегда уносят с собой энергию. Как и остальные процессы (диссоциация ядер, рождение пар и пр.), нейтринные процессы сопровождаются затратой энергии и понижением давления. Однако если раньше мы имели только изменение состояние равновесия из-за рождения новых частиц, то теперь вследствие энергетических потерь полного равновесного состояния вообще нет: $ \partial S/\partial t\neq 0$ ($ S$ -- энтропия). Энтропия иногда падает! В этом нет противоречия: падает энтропия вещества в центре ядра, но возникает энтропия нейтрино, улетевших от звезды.

Но неполное равновесие тоже можно излучать. Например, гремучий газ: $ \rm {H}_2+ \rm {O}_2$ -- мы можем рассматривать его расширение, сжатие и прочее, причем все эти процессы будут равновесными, кроме одного -- процесса сгорания. То же можно сказать и о любой смеси веществ (например, $ \rm {H}+\rm {He}$, если иметь в виду ядерные реакции), так как полное равновесие -- это ядра железа.

В состоянии полного термодинамического равновесия концентрация нейтрино пропорциональна $ T^3$. Плотность энергии и давление $ \sim$$ T^4$. Однако в звездах нейтрино рождаются и уходят, поэтому их истинная концентрация гораздо меньше равновесной.

При рассмотрении горения водорода мы уже учитывали рождение нейтрино. Но тогда учет нейтрино сводился просто к эффективному уменьшению калорийности ядерного топлива. Например, если скорость реакции

$\displaystyle 4\rm {H}\to^4\rm {He}$   равна$\displaystyle ~q~[$актов/г$\displaystyle \cdot$с$\displaystyle ], $

то нагрев

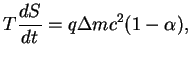
$\displaystyle T{dS\over{dt}}=q\Delta mc^2(1-\alpha), $

где $ \Delta m=4m_{\rm H}-m_{\rm He}$ -- дефект масс, а $ \alpha $ -- доля энергии, уносимой нейтрино ( $ \alpha\sim0,05\div0,1$).Но есть и другой путь рождения нейтрино -- урка-процесс, впервые рассмотренный Гамовым и Шенбергом.

Пусть имеется стабильное ядро $ {}^{3}{\mathrm{He}}$. Ядро с тем же ядерным весом -- ядро трития -- неустойчиво и распадается по схеме $ \beta$-распада,

$\displaystyle {}^{3}{\mathrm{H}}\to {}^{3}{\mathrm{He}}+e^-+\widetilde{\nu} $

с периодом полураспада (время жизни) 12 лет. При этом выделяется энергия $ \sim$18 кэВ. Когда может идти обратный процесс

$\displaystyle e^-+ {}^{3}{\mathrm{He}}\to {}^{3}{\mathrm{H}}+\nu? $

Ясно, что энергия электрона должна быть больше 18 кэВ. Скорость этого процесса $ q$ пропорциональна $ E^2_{\nu}=(E-18\;$кэВ$ )^2$:

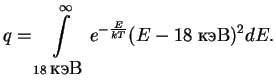
$\displaystyle q=\int\limits^{\infty}_{18\;\mbox{кэВ}}e^{-{E\over{kT}}}(E-18\;\mbox{кэВ})^2 dE. $

Главную роль играет экспоненциальный множитель $ \exp(-18\;$кэВ$ /kT)$, т.е. при комнатной температуре в скорость этого процесса входит число $ \exp({-10^6})$. Но при температуре порядка 10 кэВ ($ \sim 10^8$K) процесс может идти. Однако одновременно в таком веществе тритий опять распадается:

$\displaystyle {}^{3}{\mathrm{H}}\to {}^{3}{\mathrm{He}}+e^-+\widetilde{\nu}, $

и опять образуются $ \widetilde{\nu}$. Таким образом, и при прямом и пир обратном процессе происходят необратимые потери энергии за счет $ \nu$ и $ \widetilde{\nu}$, т.е. независимо от того, выделяется энергия или нет (в каждом отдельном процессе), нейтрино и антинейтрино уходят. Процессы такого рода Гамов и назвал урка-процессами. Поскольку скорость реакции образования трития есть $ q(T)$, в стационарных условиях должно быть(концентрации обозначаем квадратными скобками):

$\displaystyle q(T)[{}^{3}{\mathrm{He}}]={1\over{\tau}}\;[{}^{3}{\mathrm{H}}], $

где $ \tau$ -- время жизни трития $ {}^{3}{\mathrm{H}}$. Пусть в начале вещество состояло только из ядер $ {}^{3}{\mathrm{He}}$ с концентрацией $ [{}^{3}{\mathrm{He}}]_0$. Тогда при некоторой температуре $ T$ установится следующая стационарная концентрация трития:

$\displaystyle [{}^{3}{\mathrm{H}}]={q(T)\over{q(T)+1/\tau}}\;[{}^{3}{\mathrm{He}}]_0. $

Вероятность распада $ W$ (1/см$ ^3\cdot$с)

$\displaystyle W={1\over{\tau}}\;[{}^{3}{\mathrm{H}}]={1\over{\tau}}\;[{}^{3}{\mathrm{He}}]_0\;{1\over{1+1/\tau q}}. $

На первый взгляд кажется, что скорость урка-процесса выходит на константу (плато) при $ T\longrightarrow\infty$ ( $ q\longrightarrow\infty$ при $ T\longrightarrow\infty$) из-за ограничения периодом полураспада трития (рис. 49).

При высоких температурах, когда уже нет ядер, урка-процесс идет таким образом:

$\displaystyle e^-+ p=n+\nu, $

$\displaystyle n\to p+e^-+\widetilde{\nu}. $

Рис. 49.

Нейтрон тяжелее протона на 0,8 МэВ. Поэтому плато $ W=[n+p]/10^3$ с достигалось бы при $ T>0,8$ МэВ. Однако Пинаев заметил, что при таких температурах появляются позитроны $ e^+$ и начинает эффективно идти процесс

$\displaystyle e^++n\to p+\widetilde{\nu}\qquad (T>10^{10}\;$K$\displaystyle ). $

Вследствие этого число нейтронов приблизительно равно числу протонов (без учета позитронов были бы только нейтроны). Ясно, что при этом плато исчезает и кривая $ W(T)$ идет вверх.

Выпишем без расчета величину энергопотерь, связанных с обсуждаемыми процессами:

$\displaystyle Q\simeq8\cdot 10^{11}\rho T^6_9=8\cdot 10^{-43}\rho T^6\;[$эрг/см$\displaystyle \cdot$см$\displaystyle ^3]. $

В плотность вещества $ \rho $ при высокой температуре главный вклад дают нейтроны и протоны7.2. Объясним теперь, почему скорость энергетических потерь пропорциональна $ T^6$. Во-первых, при $ kT\gg m_ec^2$ концентрации электронов и позитронов примерно равны и пропорциональны $ T^3$ (поскольку массой $ e^-$ и $ e^+$ можно пренебречь, их импульс $ p=E/c\sim kT/c\sim T$, а концентрация $ n\sim p^3\sim T^3$). Во-вторых, сечение реакций $ \sigma_{e^{-}p}=\sigma_{e^{+}n}\sim T^2$. В общей теории (см. раздел 5.4) $ \sigma\sim (H')^2dN/dE$, где $ H'$ -- матричный элемент, который постоянен, так как это точечное взаимодействие, а $ N=4/3\pi P^3/(2\pi\hbar)^3$ -- число возможных состояний с импульсом меньше $ p$ в единице объема. Используя соотношение

$\displaystyle E^2=(m_ec^2)^2+c^2p^2, $

имеем

$\displaystyle E\;dE=c^2p\;dp $

и

$\displaystyle dN\sim p^2\;dp\sim p\;E\;dE, $

т.е.

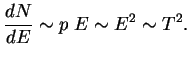
$\displaystyle {dN\over{dE}}\sim p\;E\sim E^2\sim T^2. $

Каждое нейтрино уносит с собой энергию $ E_{\nu}\sim T$. Поэтому окончательно

Рис. 50.

$\displaystyle Q\sim n\sigma E_{\nu}\sim T^3\, T^2\, T=T^6. $

У некоторых ядер может наступить насыщение, а затем уже степенной рост (рис. 50). Существование урка-процессов несомненно. Кроме этого есть еще процессы другого типа с участием нейтрино, связанные с гипотезами, которые пока не проверены экспериментально.

Для объяснения всех экспериментальных проявлений слабых взаимодействий до недавнего времени достаточно было считать, что все частицы взаимодействуют в одной точке (причем взаимодействуют -- это значит и рождаются). Например:

$\displaystyle e^-+p=n+\nu_e. $

Можно считать,что в этом процессе в одну точку приходят две частицы, из той же точки вылетают две новые частицы. Вероятность этого процесса описывается матричным элементом гамильтониана (см. раздел 5.4)

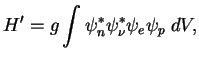
$\displaystyle H'=g\int\psi^*_n\psi^*_{\nu}\psi_e\psi_{p}\;dV, $

где $ g=1,4\cdot10^{-49}\;$эрг$ \cdot$см$ ^3$ -- постоянная слабого взаимодействия. Мы запишем самую существенную часть гамильтониана символически следующим образом:

$\displaystyle H=(\widetilde{p}n)\;(\widetilde{e}\nu_e)+(p\widetilde{n})\;(e\widetilde{\nu_e}).$ (7.2)

Здесь знак $ \sim$ (тильда) обозначает античастицу, а скобки объединяют частицы, входящие в реакцию всегда по одну сторону от стрелочки. Запись (2) расшифровывается так: если встречается символ некоторой частицы, то это обозначает гибель данной частицы, либо рождение ее античастицы. Например, первый член в (2) символизирует реакцию

$\displaystyle \widetilde{p}+n\to e^-+\widetilde{\nu_e} $

(аннигиляция нуклонов), а также:

$\displaystyle n\to p+e^-+\widetilde{\nu_e}\qquad (\beta$-распад нейтрона$\displaystyle ), $

а второй, сопряженный член, символизирует обратные процессы

$\displaystyle p+e^-\to n+\nu_e\qquad($нейтронизация$\displaystyle ), $

$\displaystyle p+\widetilde{n}\to e^++\nu_e\qquad($аннигиляция$\displaystyle ). $

В действительности есть еще реакции с мюоном $ \mu$ и мюонным нейтрино $ \nu_{\mu}$, например, распады

$\displaystyle \mu^-\to e^-+\widetilde{\nu_e}+\nu_{\mu}, $

$\displaystyle \mu^+\to e^++\nu_e+\widetilde{\nu_{\mu}}, $

или захват мюона нуклоном:

$\displaystyle \mu^-+p\to n+\nu_{\mu} $

и т.д. Все эти процессы можно описать гамильтонианом $ H=g\,[(\widetilde{p}n)\; (\widetilde{e}\nu_e)+(\widetilde{p}n)(\widetilde{\mu}\nu_{\mu})+(\widetilde{\mu}\nu_{\mu}) (\widetilde{e}\nu_e)+$сопряженные члены$ ]$. Все они характеризуются константой $ g=1,4\cdot10^{-49}$ эрг$ \cdot$см$ ^3$. Тот факт, что эта константа размерна, представляется удивительным. Он может означать, что процесс слабого взаимодействия не является элементарным и на самом деле протекает в два этапа с образованием промежуточной частицы, которую пока не наблюдали:

$\displaystyle n\to p+W^-,\qquad W^-\to e^-+\widetilde{\nu_e}. $

Из сохранения момента ясно, что эта частица должна иметь спин $ s=1$, т.е. должна быть бозоном. Процессы с $ W$-бозоном аналогичны электромагнитным процессам с фотоном:

$\displaystyle p\to p+\gamma,\quad \gamma\to e^-+e^+. $

Теория $ W$-бозона предполагает, что он во всем, кроме большой массы, похож на фотон. В этом случае элементарные взаимодействия с $ W$-бозоном характеризуются той же безразмерной константой, что и электромагнитное взаимодействие (постоянной тонкой структуры):

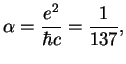
$\displaystyle \alpha={e^2\over{\hbar c}}={1\over{137}}, $

а ``слабость'' слабого взаимодействия объясняется тем, что при обычных энергиях $ W$-бозон появляется только виртуально из-за своей большой массы. Значение массы $ W$-бозона $ M_W$ можно оценить из экспериментального значения постоянной слабого взаимодействия $ g$ и размерных соображений:

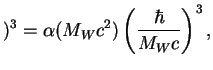
$\displaystyle g=\alpha\cdot$энергия$\displaystyle \cdot($длина$\displaystyle )^3=\alpha(M_Wc^2)\left({\hbar\over {M_Wc}}\right)^3, $

откуда

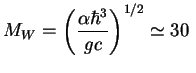$\displaystyle M_W=\left({\alpha\hbar^3\over{gc}}\right)^{1/2}\simeq 30\;$ГэВ$\displaystyle \simeq 30\;m_{p}. $

Расстояние, которое проходит $ W$-бозон до распада, можно оценить из соотношения неопределенностей

$\displaystyle x\sim \hbar/M_Wc\simeq 10^{-15}\;$см$\displaystyle . $

Малость этого расстояния (на два порядка меньше радиуса ядерных сил!) и позволяла старой теории считать слабое взаимодействие точечным.

Квантовомеханическая амплитуда процессов с рождением $ W$-бозона должна иметь вид

$\displaystyle J=(\widetilde{p}n)\widetilde{W}+(e\widetilde{\nu_e})\widetilde{W} +(\mu\widetilde{\nu_{\mu}})\widetilde{W}. $

По общим принципам квантовой механики полная амплитуда процессов, идущих через промежуточный $ W$-бозон, равна произведению амплитуды образования, $ J$, на амплитуду распада $ W$, которая, очевидно, равна $ J^*$, т.е. сопряженна $ J$:

$\displaystyle J^*=W(p\widetilde{n})+W(\widetilde{e}\nu_e)+W(\widetilde{\mu}\nu_{\mu}). $

Гамильтониан наблюдаемых процессов тогда выглядит следующим образом:

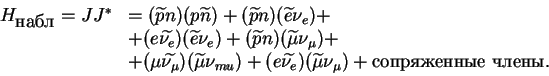
\begin{displaymath} \begin{array}{ll} H_{\mbox{набл}}=JJ^*&=(\widetilde{p}n)(p\w... ...etilde{\mu}\nu_{\mu}) +\mbox{сопряженные члены.}\cr \end{array}\end{displaymath}

Произведение $ \widetilde{W}W$, обозначающее рождение и гибель $ W$, войдет просто в константу слабого взаимодействия $ g$, которую мы опускаем в символической записи гамильтониана. Процессы, стоящие в правом столбце этого выражения, давно уже наблюдались в лаборатории. В последнее время обнаружены и процессы, записанные в левом столбце.

Процесс $ (\widetilde{p}n)(p\widetilde{n})$, т.е. $ p+n\rightleftarrows p+n$ -- это рассеяние нуклонов за счет слабого взаимодействия. Его наблюдать трудно, так как есть рассеяние за счет сильного взаимодействия. Но слабое взаимодействие приводит к несохранению четности, и в этих процессах, например, должны появляться $ \gamma$-кванты с круговой поляризацией.

Процесс $ (e\widetilde{\nu_e})(\widetilde{e}\nu_e)$ -- рассеяние нейтрино на электронах:

$\displaystyle e^-+\nu_e\rightleftarrows e^-+\nu_e. $

Мы можем переставлять частицы справа налево с заменой их на античастицы:

$\displaystyle e^-+e^+\rightleftarrows \nu_e+\widetilde{\nu_e}, $

$\displaystyle e^+\rightleftarrows e^-+\nu_e+\widetilde{\nu_e}. $

Процесс

$\displaystyle e^-+\nu_e\rightleftarrows e^-+\nu_e $

наблюдать очень трудно, гораздо сложнее процесса $ \nu_e+p\rightleftarrows n+e^+$, который уже наблюдался.

Интересно, что Райнес в свое время дал для процесса $ (e\widetilde{\nu_e})(\widetilde{e}\nu_e)$ экспериментальное значение сечения $ \sigma_{\mbox{эксп}}=500\;\sigma_{\mbox{теор}}$, но это оказалось ошибкой. Сейчас

$\displaystyle \sigma_{\mbox{эксп}}=(1\pm 1)\,\sigma_{\mbox{теор}}. $

Если бы было $ \sigma_{\mbox{эксп}}=500\;\sigma_{\mbox{теор}}$, то этого не допустила бы астрофизика.

Процесс

$\displaystyle e^-\to e^-+\nu+\widetilde{\nu} $

не идет на свободном электроне по законам сохранения. Он идет в поле ядра:

$\displaystyle e^-+Z\to Z+e^-+\nu+\widetilde{\nu} $

и уносит энергию, так как $ \nu\widetilde{\nu}$ улетают.

Если ``раскачивать'' кусок вещества, то электромагнитные волны он излучать не будет, так как вещество электронейтрально, но данный нейтринный процесс может идти, так как он не компенсируется протонами, т.е. при колебании вещества возникает нейтринное излучение.

Данный вид взаимодействия приводит к тому, что между любыми двумя телами есть дальнодействующая сила, потенциал которой пропорционален $ \varphi=1/r^5$.

В гамильтониане есть член

$\displaystyle g(e\widetilde{\nu_e})(\widetilde{e}\nu_e), $

где $ g=1,4\cdot10^{-49}$ эрг$ \cdot$см$ ^3$ -- константа слабого взаимодействия, т.е. энергия нейтрино зависит от плотности электронов в данном месте. Потенциальная яма, рассчитанная на одно нейтрино, составит (для свинца)

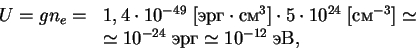
\begin{displaymath} \begin{array}{ll} U=gn_e=&1,4\cdot10^{-49}\;[\mbox{эрг}\cdot... ...q10^{-24}\;\mbox{эрг}\simeq 10^{-12}\;\mbox{эВ},\cr \end{array}\end{displaymath}

т.е. появляется коэффициент преломления вещества для нейтрино.

Есть и другие процессы с излучением нейтрино. Это плазменные колебания с испусканием нейтринно-антинейтринных пар. На стадии горения углерода нейтринное излучение может быть равно фотонному.

Наконец, при высокой температуре ($ T>10^{10}$ K) самым главным становится процесс $ e^++e^-\to\nu+\widetilde{\nu}$ (он остается сравнимым с урка-процессом Пинаева).

Пары $ \nu\widetilde{\nu}$ в этом процессе рождаются с вероятностью гораздо меньшей, чем пары $ \gamma$-квантов в процессе

$\displaystyle e^+e^-\to\gamma+\gamma, $

но последний процесс идет в прямую и обратную стороны и не влияет на вероятность первого. При очень высоких температурах скорость энергопотерь определяется выражением

$\displaystyle Q\sim4\cdot10^{15}\cdot T^9_9\;[$эрг/с$\displaystyle \cdot$см$\displaystyle ^3]. $

Легко понять, откуда появилась высокая -- девятая степень температуры:

$\displaystyle Q\sim n_{e^-}n_{e^+}\sigma E\sim T^3\,T^3\,T^2\,T=T^9. $

При низкой температуре

$\displaystyle n_{e^-}n_{e^+}\equiv[e^+][e^-]\sim\exp(-2m_ec^2/kT)\sim e^{-12/T_9}. $

Отметим принципиально новые результаты семидесятых годов в области слабого взаимодействия и их астрофизическое значение.

В 1974 г. был открыт третий член ряда, первые два которого представляют собой электрон и мюон. Эта частица обозначается $ \tau$ и называется тау-лептон. Физика вступает в противоречие с филологией: лептон по-гречески значит ``легкий'', и это было правильно применительно к $ e^{\pm}$ и $ \mu^{\pm}$. Масса $ \tau$ равна 1780 МэВ, т.е. он в 1,9 раза тяжелее протона, легким его назвать нельзя. Но свойства $ \tau$ подобны свойствам $ e$ и $ \mu$. Поэтому, придавая слову ``лептон'' новый смысл -- ``фермион, обладающий слабым и электромагнитным, но не сильным, взаимодействиями'', мы называем $ \tau$ лептоном. Предполагается, что существует и соответствующее этому лептону нейтрино, $ \nu_{\tau}$, а также его античастица $ \widetilde{\nu_{\tau}}$, подобно тому как мюону соответствует $ \nu_{\mu}$ и $ \widetilde{\nu_{\mu}}$. Следовательно, распады $ \tau$ идут так: $ \tau^-=\mu^-+\nu_{\tau}+\widetilde{\nu_{\mu}}$ или $ \tau^+=\pi^++\nu_{\tau}$. Распад с образованием пионов и других адронов невозможен для мюона, но возможен для тау-лептона благодаря большой массе этой частицы.

Второе открытие -- существование нейтрального тока. Процессы, протекающие через посредство промежуточных бозонов $ W^{\pm}$, называют зависимыми от заряженного тока. Феноменологически эти процессы записаны так, что каждый член в выражении для тока (в наших обозначениях для амплитуды $ J$) меняет заряд на единицу, а общий заряд сохраняется, потому что гамильтониан содержит произведение двух токов, одного уменьшающего и другого увеличивающего заряд. Но в теории Салама-Вейнберга предполагается, что наряду с $ W^{\pm}$ существует аналогичный тяжелый векторный (спин 1) промежуточный (в слабом взаимодействии) и притом нейтральный $ Z^0$ бозон. Будучи нейтральным, он должен распадаться на пары нейтрино-антинейтрино или пары заряженных частиц или античастиц: $ Z^0\rightleftarrows \nu_e+\widetilde\nu_e$, $ Z^0\rightleftarrows e^++e^-\ldots$  Аналогично этому происходит и взаимодействие с адронами7.3. Как всегда в таких формулах можно перенести античастицу справа налево, превращая ее в частицу. У самого $ Z^0$-бозона нет античастицы, или точнее он сам является своей античастицей, так как $ Z^0$ истинно нейтрален, также как фотон.

На опыте при энергиях, недостаточных для реального рождения $ Z^0$-бозона (такая ситуация продлится вероятно до 1985 г.), наблюдаются процессы типа рассеяния: $ \nu_{\mu}+p\to Z^0\to\nu_{\mu}+p$. Предсказывается также слабое взаимодействие электронов с ядрами, которое обнаруживается при рассеянии релятивистских электронов, а также в оптическом поведении атомов. Это взаимодействие качественно было предсказано одним из авторов (Я.Б.Зельдовичем) еще в 1958 г. В настоящее время его можно считать доказанным.

Каковы астрофизические следствия существования нейтрального тока?

С одной стороны, расширяются возможности производства пар нейтрино-антинейтрино. Теперь возможны процессы

$\displaystyle e^-+e^+\to Z^0\to\nu_{\mu}+\widetilde{\nu_{\mu}}, $

$\displaystyle e^-+e^+\to Z^0\to\nu_{\tau}+\widetilde{\nu_{\tau}}. $

Возможно также рождение пар $ \nu,\;\widetilde{\nu}$ при столкновении адронов или возбужденными состояниями ядер $ A^*\to A+Z^0\to A+\nu+\widetilde{\nu}$ ($ \nu_e$, $ \nu_{\mu}$, $ \nu_{\tau}$ -- с одинаковой вероятностью). С другой стороны, появляется новый канал рассеяния нейтрино на электронах и , главное, новый процесс рассеяния нейтрино на ядрах. В этом процессе рассеяние на всех нуклонах может происходить когерентно, при этом амплитуда рассеянной волны пропорциональна числу нуклонов, а сечение рассеяния оказывается пропорционально квадрату числа нуклонов. Таким образом увеличивается непрозрачность плотного вещества, состоящего из тяжелых и средних ядер по отношению к нейтрино всех сортов. Этот факт играет большую роль в теории взрыва сверхновых звезд.

Какова роль нейтринных процессов в эволюции звезд вообще? На стадии главной последовательности нейтринное излучение, казалось бы, малосущественно. Однако нельзя забывать, что, во-первых, без слабого взаимодействия, а значит и без излучения нейтрино, вообще не возможно горение водорода. А, во-вторых, нейтрино позволяет в принципе заглянуть в самые центральные области звезд и проверить наши теории. Для Солнца это уже делается (опыты Дэвиса).

На поздних стадиях эволюции нейтринное излучение может играть решающую роль, поскольку достигаются высокие температуры, и нейтрино эффективно отводит тепло. Без нейтрино трудно объяснить образование планетарных туманностей, взрывы сверхновых. Нейтринное излучение сильно ускоряет остывание горячих белых карликов и нейтронных звезд. Поэтому, сравнивая предсказания теории эволюции звезд, рассчитанные с учетом и без учета нейтрино, с наблюдениями реальных объектов, можно проверить теорию слабых взаимодействий, т.е. установить наличие в природе тех процессов, которые в лаборатории пока не наблюдались.

<< 7.3 Два типа энергетических ... | Оглавление | 8. Введение в OTO >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 120]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования