Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Физические основы строения и эволюции звезд
<< 7.2 Нейтронизация | Оглавление | 7.4 Роль нейтрино в ... >>

7.3 Два типа энергетических потерь

Обычная звезда находится в гидростатическом равновесии, при котором силы тяготения уравновешены градиентом давления. Если нет вырождения, то давление тепловое. Потери энергии звездой приводят к тому, что состояние равновесия все время изменяется. При этом надо различать два принципиально разных типа энергетических потерь -- обратимые и необратимые.

1. Процессы, при которых происходят однократные потери энергии, т.е. процессы типа ионизации, диссоциации, рождение пар $ e^+,\;e^-$ и т.п. являются обратимыми. После того как произошло превращение, потери энергии прекращаются. Такие процессы можно характеризовать величиной $ E\;[$эрг/г$ ]$, т.е. количеством энергии, которую нужно затратить, чтобы перевести вещество в новое состояние.

2. Процессы, при которых образуются частицы, способные уходить из системы и уносить энергию, являются необратимыми. Типичными примерами является рождение пар $ \gamma$ -квантов и особенно пар нейтрино-антинейтрино. Звезды почти всегда практически прозрачны для нейтрино. На конечных стадиях эволюции потери энергии через нейтринные процессы являются преобладающими. Процессы такого типа характеризуются величиной $ Q\;[$эрг/г$ \cdot$с$ ]$, т.е. энергией, теряемой граммом вещества в секунду.

Рассмотрим более подробно обратимые потери. Этот тип потерь лучше назвать не потерями , а особенностями уравнения состояния. Рассмотрим уравнение состояния $ P(\rho, S)$, где $ S$ -- удельная энтропия для идеального газа, состоящего из атомарного водорода.

При низкой температуре ( $ T<T_{\mbox{иониз}}$)

$\displaystyle S=-{\cal R}\;\ln\rho+\frac{3}{2}\;{\cal R}\;\ln T+K_{\rm H}, $

$ {\cal R}$ -- универсальная газовая постоянная, а $ K_{\rm H}$ -- так называемая химическая константа водорода.

При высокой температуре, когда весь водород ионизован, газ состоит из двух компонент -- протонной и электронной. Поскольку энтропия аддитивна, получаем

$\displaystyle S=-{\cal R}\;\ln\;\rho_e+{3\over 2}\;{\cal R}\ln\;T_e+K_e-{\cal R}\;\ln\;\rho_p+{3\over2} \;{\cal R}\;\ln\;T_p+K_{p}, $

где $ K_e$ и $ K_p$ -- химические константы электронного и протонного газов. Так как статические и атомные веса H и $ p$ почти равны, имеем $ K_p\simeq K_H$.

Из первого соотношения мы видим, что

$\displaystyle T=e^{-2K_H/3{\cal R}}\;e^{2S/3{\cal R}}\;\rho^{2/3}. $

Таким образом, при постоянной энтропии $ T\sim \rho^{2/3}$, а давление

$\displaystyle P={{\cal R}\;\rho\;T\over{\mu}}=B_1\,\rho^{5/3},\qquad B_1\sim e^{{2\over3}\;{S\over {\cal R}}}.$ (7.1)

С другой стороны, при $ T\gg T_{\mbox{иониз}}$

$\displaystyle P=B_2\rho^{5/3},\qquad B_2\sim e^{{1\over3}\;{S\over{\cal{R}}}}, $

т.е. есть и до и после ионизации наклон прямой в переменных $ \lg P\;$-$ \;\lg\rho$ один и тот же и равен 5/3. Но в промежуточной области мы имеем почти изотермический участок, где $ P\sim\rho$ (рис. 46). Ионизация происходит в узком интервале температур , поскольку по Саха

$\displaystyle [p][e^-]/[\mathrm{H}]\sim e^{-J/kT}, $

где $ J$ -- потенциал ионизации.

Рис. 46.Рис. 47.

По другому это можно понять, если вспомнить, что в неионизованном газе $ C_V\,dT=-P\,dV$, $ E=C_V T$, откуда

$\displaystyle P={2\over3\,\rho\, C_V T}. $

После ионизации $ E=C_V T+J/m_p$. Из-за того, что часть работы уходит на ионизацию, давление оказывается ниже, чем по формуле (7.1).

Теперь займемся фигурами равновесия. Рассмотрим водородную самогравитирующую конфигурацию, когда ионизация еще не произошла (модель протозвезды). Ясно, что при этом происходит сжатие, и на графике $ \lg P\;$-$ \;\lg\rho$ появляются три равновесных решения, два из которых устойчивы, а одно неустойчиво (см. рис. 47) 7.1. При еще более низких энтропиях ( меньших $ S_3$) остается одно устойчиво состояние. Ясно, что переход из одного устойчивого состояния в другое происходит скачком.

Все это происходит при температурах $ \sim 10^4$К$ \sim 1$ эВ, т.е. при температурах, гораздо меньших потенциала ионизации ( $ J\sim 13,6$ эВ). В формуле Саха экспонента мала, но велик предэкспоненциальный множитель.

Теперь рассмотрим другой механизм потери устойчивости, который важен при температурах $ \sim$ 0,5 МэВ. Это механизм фотодиссоциации железа, впервые рассмотренный Хойлом и Фаулером:

$\displaystyle \gamma + {}^{56}{\mathrm{Fe}}\to {}^{52}{\mathrm{Cr}}+\alpha. $

Если уж началась диссоциация железа, то разваливаются и другие элементы, вплоть до гелия. На частицу при этом поглощается энергия $ \sim$7МэВ. Всего получается 17 частиц (13 $ {}^{4}{\mathrm{He}}+4n$). Таким образом полная энергия диссоциации составляет $ J=17\times 7=120$МэВ на ядро $ {}^{56}{\mathrm{Fe}}$. Однако фотодиссоциация начинается при температурах $ kT\ll J$ опять же из-за большой величины предэкспоненциального множителя в формуле Саха. Этот множитель, который описывает статистический вес диссоциированного состояния, велик, так как образуется много частиц.

В качестве примера приведем два значения $ T_{\mbox{дис}}$ при разных плотностях:

$ \rho\;($г/см$ ^3)$ $ 10^3$ $ 10^6$
$ T_{\mbox{дис}}\;$(K) $ 4,1\cdot10^9$ $ 5,8\cdot10^9$
$ T_{\mbox{дис}}\;$(МэВ) 0,35 0,50

В результате фотодиссоциации железа происходит потеря устойчивости и звезда начинает быстро (за гидродинамическое время) сжиматься. Этот процесс подобен взрыву, но движение вещества направлено внутрь, поэтому он называется имплозией (в отличие от обычного взрыва ``explosion''). Кривые на плоскости $ \lg P\;$-$ \;\lg\rho$ при этом подобны изображенным на рис. 47.

Поскольку во внешних слоях звезды могут оставаться несгоревшие элементы (C, O и пр.), а при имплозии происходит сильный нагрев вещества, то возможно выделение ядерной энергии, при котором имплозия сменяется обычным взрывом, направленным наружу. Раньше думали, что этот механизм может объяснить взрыв звезд с массой $ M>10\;M_\odot$ как сверхновых, однако самые последние расчеты показывают, что имплозия не сменяется взрывом. Энергия уходит из звезды в виде нейтрино (см. раздел 7.4).

В заключение рассмотрим случай, когда в термодинамическом равновесии может находиться большое количество электронно-позитронных пар. Пусть давление излучения $ \sim$$ a T^4$ много больше давления вещества $ {\cal R}\rho T$, но плотность вещества все еще больше плотности излучения:

$\displaystyle \rho>aT^4/c^2. $

Из термодинамического соотношения

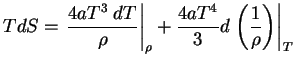
$\displaystyle TdS=\left.{4aT^3\;dT\over {\rho}}\right\vert _{\rho}+{4aT^4\over 3}d\left.\left( {1\over{\rho}}\right)\right\vert _T $

найдем удельную энтропию

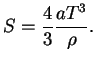
$\displaystyle S={4\over3}{aT^3\over{\rho}}. $

Итак,

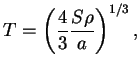
$\displaystyle T=\left({4\over3}{S\rho\over a}\right)^{1/3}, $

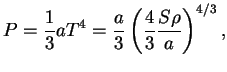
$\displaystyle P={1\over3}aT^4={a\over3}\left({4\over3}{S\rho\over a}\right)^{4/3}, $

т.е. для чистого излучения при постоянной энтропии $ P\sim \rho^{4/3}$.

Рис. 48.

При температурах $ kT>m_ec^2$ начинается интенсивное рождение пар ($ e^+e^-$). В предельном случае $ kT\gg m_ec^2$ кроме излучения имеется равновесный релятивистский электронно-позитронный газ. Полная плотность энергии при этом

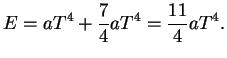
$\displaystyle E=aT^4+{7\over4}aT^4={11\over4}aT^4. $

Давление

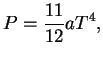
$\displaystyle P={11\over{12}}aT^4, $

и энтропия

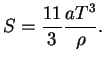
$\displaystyle S={11\over3}{aT^3\over{\rho}}. $

Таким образом, при $ kT\gg m_ec^2$ снова $ P\sim \rho^{4/3}$, но в промежуточном случае наклон кривой на графике $ \lg P\;$-$ \;\lg\rho$ должен быть меньше 4/3 (см. рис. 48). При относительно небольших плотностях, когда давление определялось фотонным газом, звезда уже была на границе устойчивости ( $ P\sim \rho^{4/3}$). Поэтому при подходе к области рождения электрон-позитронных пар уже нет состояния равновесия. Поэтому нет сверхмассивных звезд.


<< 7.2 Нейтронизация | Оглавление | 7.4 Роль нейтрино в ... >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 120]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования