<< 6.6 Определение возраста скоплений | Оглавление | 7. Новые физические факторы... >>
6.7 Качественная картина эволюции звезды
Эволюция звезд с массой больше и меньше 2,5![]() идет по-разному.
При
идет по-разному.
При
![]() в изотермическом гелиевом ядре растет температура и в
дальнейшем возможно зажигание и спокойное горение гелия. Для звезд с меньшей массой
в изотермичесом ядре наступает вырождение, при котором сила тяжести уравновешивается
давлением вырожденных электронов. Если в таком ядре начнутся ядерные реакции, то при
его достаточно большой массе может произойти термоядерный взрыв, так как повышение
температуры почти не будет сопровождаться одновременным повышением давления. При массах
в изотермическом гелиевом ядре растет температура и в
дальнейшем возможно зажигание и спокойное горение гелия. Для звезд с меньшей массой
в изотермичесом ядре наступает вырождение, при котором сила тяжести уравновешивается
давлением вырожденных электронов. Если в таком ядре начнутся ядерные реакции, то при
его достаточно большой массе может произойти термоядерный взрыв, так как повышение
температуры почти не будет сопровождаться одновременным повышением давления. При массах
![]() наступает вырождение углерода в центре. Возможны
условия, когда углеродное ядро звезды сгорает почти мгновенно и может быть достигнута
светимость
наступает вырождение углерода в центре. Возможны
условия, когда углеродное ядро звезды сгорает почти мгновенно и может быть достигнута
светимость ![]()
![]() . Такой взрыв может быть отождествлен со
вспышкой сверхновой.
. Такой взрыв может быть отождествлен со
вспышкой сверхновой.
В этом разделе мы хотим на простых формулах (хотя и приближенных) показать, как в результате эволюции, из-за вырождения в центре, теплоемкость звезды может стать положительной, и возникает тепловая неустойчивость.
Вся суть в том, что мы рассматриваем эволюцию звезды с данной массой, причем ![]() и
и ![]() связаны между собой условиями гидростатического равновесия. Эволюция постепенно
меняет связь между
связаны между собой условиями гидростатического равновесия. Эволюция постепенно
меняет связь между ![]() и
и ![]() . При этом нельзя забывать, что звезда является
протяженной, неоднородной системой, поэтому необходимо говорить либо о средних
значениях
. При этом нельзя забывать, что звезда является
протяженной, неоднородной системой, поэтому необходимо говорить либо о средних
значениях ![]() и
и
![]() , либо о значениях в центре
, либо о значениях в центре ![]() и
и ![]() . Ниже для
определенности будем рассматривать
. Ниже для
определенности будем рассматривать ![]() и
и ![]() .
.
Структуру звезды можно приближенно описать политропой. Пусть индекс политропы ![]() .
Тогда
.
Тогда
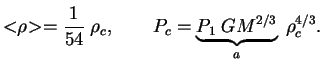
Рассмотрим сначала предельный случай вырожденного электронного газа с ![]() .
Тогда давление связано с плотностью по формуле
.
Тогда давление связано с плотностью по формуле
![$\displaystyle \cdot \rho\;\Bigl[\underbrace{\left((m_ec^2)^2+p_{\mbox{\sc f}}^2c^2
\right)^{1/2}}_{E_{\mbox{\sc f}}}-m_ec^2\Bigr],
$](https://images.astronet.ru/pubd/2008/02/15/0001226214/img1364.gif)
![$\displaystyle P\sim\rho\;\left[\left((m_ec^2)^2+b\rho^{2/3}\right)^{1/2}-m_ec^2\right]\,.
$](https://images.astronet.ru/pubd/2008/02/15/0001226214/img1369.gif)
![$\displaystyle P\sim \rho \,\left[\left((m_ec^2)^2+b\rho^{2/3}+f(T)\right)^{1/2}-m_ec^2\right]=a\rho^{4/3}.$](https://images.astronet.ru/pubd/2008/02/15/0001226214/img1370.gif) |
(6.2) |
Здесь
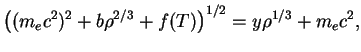
При больших плотностях поведение температуры зависит от того, положительна или
отрицательна скобка ![]() при
при
![]() .
Если
.
Если ![]() (т. е. масса мала,
(т. е. масса мала,
![]() и скобка отрицательна),
то легко увидеть, что существует равновесие при
и скобка отрицательна),
то легко увидеть, что существует равновесие при
![]() , и кроме этого
есть максимум температуры
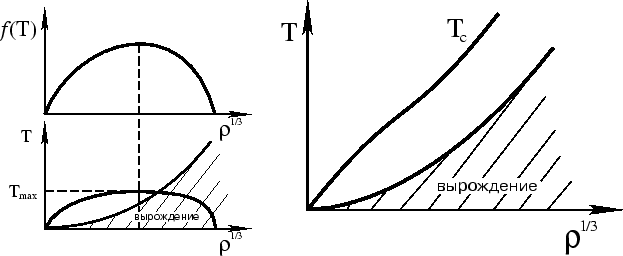
(рис. 40).
Легко найти соотношение между максимальной
плотностью (
, и кроме этого
есть максимум температуры
(рис. 40).
Легко найти соотношение между максимальной
плотностью (![]() ) и плотностью, соответствующей максимуму температуры:
) и плотностью, соответствующей максимуму температуры:
![]() (так как
(так как
![]() ).
Таким образом, мы
видим, что при постепенном сжатии температура растет, достигает максимума, а
затем убывает. Найдем асимптотику
).
Таким образом, мы
видим, что при постепенном сжатии температура растет, достигает максимума, а
затем убывает. Найдем асимптотику ![]() для малых масс. Имеем
для малых масс. Имеем
При
![]() образуются белые карлики. Массы
наблюдаемых белых карликов
образуются белые карлики. Массы
наблюдаемых белых карликов ![]()
![]() . Но звезда с массой
. Но звезда с массой
![]()
![]() живет на главной последовательности около
живет на главной последовательности около
![]() лет,
т.е. больше возраста Вселенной. Это еще один аргумент в пользу того, что
наблюдаемые сейчас белые карлики произошли из более массивных звезд, которые в
процессе эволюции потеряли значительную часть своей массы. Кроме того, имеются
двойные звездные системы, состоящие из белого карлика с массой порядка
лет,
т.е. больше возраста Вселенной. Это еще один аргумент в пользу того, что
наблюдаемые сейчас белые карлики произошли из более массивных звезд, которые в
процессе эволюции потеряли значительную часть своей массы. Кроме того, имеются
двойные звездные системы, состоящие из белого карлика с массой порядка
![]() ,
и звезды главной последовательности с массой порядка
,
и звезды главной последовательности с массой порядка
![]() .
Такое сочетание объектов возможно только лишь в том случае, если на месте белого
карлика ранее была более массивная звезда, потерявшая на стадии красного гиганта
большую часть своей массы. Почти вся утерянная масса может быть захвачена вторым
компонентом.
.
Такое сочетание объектов возможно только лишь в том случае, если на месте белого
карлика ранее была более массивная звезда, потерявшая на стадии красного гиганта
большую часть своей массы. Почти вся утерянная масса может быть захвачена вторым
компонентом.
Теперь рассмотрим случай больших масс
![]() -- чандрасекаровский
предел). Для этих масс в рамках наших приближенных расчетов нет ограничений на
рост плотности и температуры
(рис. 41).
Загорание тяжелых элементов (C, O, Mg)
начинается в невырожденных условиях. Но следует помнить, что мы предполагали
постоянство числа электронов, неизменность химического состава, не учли эффекты ОТО.
На самом деле из-за этих эффектов при достижении некоторой критической плотности
начнутся катастрофические события.
-- чандрасекаровский
предел). Для этих масс в рамках наших приближенных расчетов нет ограничений на
рост плотности и температуры
(рис. 41).
Загорание тяжелых элементов (C, O, Mg)
начинается в невырожденных условиях. Но следует помнить, что мы предполагали
постоянство числа электронов, неизменность химического состава, не учли эффекты ОТО.
На самом деле из-за этих эффектов при достижении некоторой критической плотности
начнутся катастрофические события.
Задача. Расчет космологических моделей дает содержание дейтерия относительно
водорода ![]() -
-![]() . Найти значение массы звезды, при которой пойдет реакция
. Найти значение массы звезды, при которой пойдет реакция
<< 6.6 Определение возраста скоплений | Оглавление | 7. Новые физические факторы... >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |