Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Физические основы строения и эволюции звезд
<< 1.8 Теорема вириала | Оглавление | 2.2 Основные параметры политропы >>

2. Аналитическая теория политропных шаров (теория Лейна-Риттера-Эмдена)


Разделы

2.1 Уравнение Эмдена

В этой главе мы будем изучать равновесные конфигурации звезд, подчиняющихся степенному (политропному) уравнению состояния

$\displaystyle P=K\rho^\gamma=K\rho^{1+{1\over n}}, $

где $ \gamma$ -- показатель, $ n$ -- индекс политропы. Интерес к этому уравнению состояния возник еще в прошлом веке, когда думали, что все звезды полностью конвективны. При этом можно предположить, что энтропия постоянна. Интегрируя термодинамические равенства

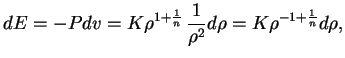
$\displaystyle dE=-Pdv=K\rho^{1+{1\over n}} {1\over \rho^2}d\rho=K\rho^{-1+{1\over n}}d\rho, $

получаем выражение для внутренней энергии

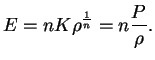
$\displaystyle E=nK\rho^{1\over n}=n{P\over \rho}. $

Отсюда энтальпия

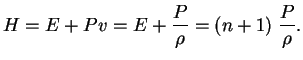
$\displaystyle H=E+Pv=E+{P\over \rho}=(n+1)\;{P\over \rho}. $

В случае идеального газа известно, что ($ c_v$ -- теплоемкость, $ {\cal{R}}$ -- газовая постоянная)

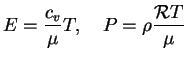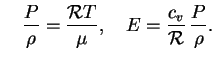
$\displaystyle E={c_v\over \mu}T, \quad P=\rho {{\cal{R}}T\over \mu}$   или$\displaystyle \quad {P\over \rho}= {{\cal{R}}T\over \mu}, \quad E={c_v\over {\cal{R}}} {P\over \rho}. $

Для одноатомного газа

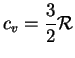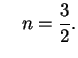
$\displaystyle c_v={3\over 2}{\cal{R}}$   и$\displaystyle \quad n={3\over 2}. $

То же можно вычислить и для многоатомных газов, но этот случай неинтересен: сейчас мы знаем о звездах несколько больше, чем 100 лет назад.

Введем переменную $ \Theta$ таким образом, чтобы

$\displaystyle \rho=\lambda \Theta^n, \quad P=K \lambda^{1+{1\over n}} \Theta^{n+1}, $

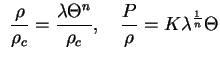   т.е. имеем$\displaystyle  {\rho\over \rho_c}={\lambda \Theta^n\over \rho_c}, \quad {P\over \rho}=K\lambda^{1\over n}\Theta$   и$\displaystyle \quad H=(n+1)K\lambda^{1\over n} \Theta. $

Для идеального газа с постоянной теплоемкостью величина $ \Theta$ пропорциональна температуре. Возьмем условие равновесия в виде

$\displaystyle \varphi+H=$const$\displaystyle $

и подействуем на него оператором $ \Delta$. Лапласиан $ \varphi$ есть $ 4\pi G \rho$, т.е. $ \Delta \varphi=4\pi G \lambda \Theta^n$, а лапласиан $ H$ есть $ (n+1)K\lambda^{1/n}\Delta \Theta $, и уравнение равновесия запишется в виде

$\displaystyle 4\pi G \lambda \Theta^n+(n+1)K\lambda^{1/n}\Delta \Theta=0 . $

Будем упрощать полученное соотношение, изменяя масштаб, т.е. вводя переменную $ \xi$ через соотношение $ r=\alpha \xi$,

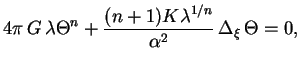
$\displaystyle 4\pi G \lambda \Theta^n+{(n+1)K\lambda^{1/n}\over \alpha^2} \Delta_\xi \Theta=0, $

где $ \Delta_\xi={1\over \xi^2} {\partial\over \partial \xi} \xi^2 {\partial\over \partial \xi}$.

Выберем $ \alpha $ так, чтобы $ 4\pi G \lambda=(n+1)K\lambda^{1/n}/\alpha^2$. Тогда уравнение равновесия запишется в виде

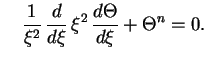
$\displaystyle \Delta_\xi \Theta+\Theta^n=0 ,$   или$\displaystyle \quad{1\over \xi^2} {d\over d \xi} \xi^2 {d \Theta\over d \xi}+\Theta^n=0. $

\begin{wrapfigure}{r}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f12.ai}\hss} \end{wrapfigure}
Рис. 12.

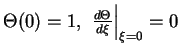Таким образом, при данном $ n$ уравнение равновесия одно и то же для звезд любой массы. Решая уравнение при граничных условиях $ \Theta(0)=1, \;\left.{d \Theta \over d \xi}\right\vert _{\xi=0}=0$ (т.е. положив $ \lambda=\rho_c$), получим монотонное убывание $ \Theta$ от единицы к нулю (рис. 12). Значение $ \xi_1$, где $ \Theta(\xi_1) =0$, является границей звезды. Плотность $ \rho $, пропорциональная $ \Theta^n$, при $ n>1$ спадает более круто, чем $ \Theta$. Мы уже показывали в разделе 1.5, что при степенном уравнении состояния на краю звезды $ \rho \sim (R-r)^{1/(\gamma-1)}$. Но $ \gamma=1+1/n$, т.е. $ \rho \sim (R-r)^n \sim \Theta^n$. Поэтому $ \Theta \sim (\xi_1-\xi)$ и вблизи $ \xi=\xi_1$ величина $ \Theta$ проходит нуль с конечной производной, хотя $ \Theta^n$ ``стелется'' (при $ n>1$), т.е. подходит к нулю, касаясь оси абсцисс.

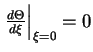Ясно, что для звезд с различными $ \rho_c$ и $ K$ кривые с одинаковыми $ n$ подобны. Достаточно знать только одну функцию $ \Theta(\xi)$. Подчеркнем важность граничного условия $ \left.{d \Theta\over d \xi}\right\vert _{\xi=0}=0$. Обратное 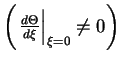$ \left(\left.{d \Theta\over d \xi}\right\vert _{\xi=0} \ne 0\right)$ означало бы конечный скачок ускорения в центре (т.е. особенность)2.1.

Несколько авторов в прошлом веке численно проинтегрировали уравнение для различных $ n$. В частности, Эмден получил таблицы $ \Theta_n(\xi)$ c большой точностью. Значение этих вычислений теперь невелико, так как расчет реальных звезд проводится с учетом физических факторов, совершенно не учитываемых в политропной теории (нестепенное уравнение состояния; истинная связь $ P$ и $ \rho $ получается из рассмотрения всех процессов, включая перенос излучения, ядерные реакции). Однако для качественных исследований решение уравнений Эмдена весьма полезно. Например, с помощью политропной модели легко показать невозможность существования сверхмассивных звезд. Это важно для проблемы квазаров.

<< 2. Политропные шары | Оглавление | 2.2 Основные параметры политропы >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 120]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования