
<< 2.4 Теория белых карликов
| Оглавление |
3. Перенос излучения в звездах >>
Теперь рассмотрим другой предельный случай, в котором главную роль играет давление
излучения.
Напомним уравнение состояния для идеального газа
здесь
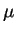
-- молекулярный вес вещества, т.е. величина, которая показывает, сколько
единиц атомного веса приходится на одну частицу (отличайте
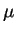
от
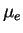
!).
Например,
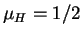
, но
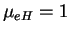
, и
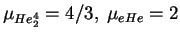
и т.п.
При высоких температурах, когда газ полностью ионизован и является одноатомным,
тепловая энергия грамма вещества равна
С другой стороны, при высоких температурах в термодинамике звезды все большую роль
начинает играть давление излучения. Для излучения, находящегося в термодинамическом
равновесии (планковского излучения), плотность энергии однозначно определяется
температурой (см. ниже, в
разделе 3.3)
Давление при этом
В лабораторных условиях изменяют не плотность
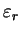
, а поток лучистой
энергии
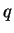
(Почему?), который связан с
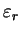
простой зависимостью
(Получите коэффициент 1/4 в этой формуле.) Таким образом,
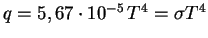
(закон Стефана-Больцмана). По формуле Эйнштейна плотность массы
излучения
Имеется широкая область астрофизических условий, когда давление и энергия излучения
и вещества сравнимы, но плотность массы излучения много меньше плотности массы
вещества (
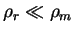
). Выпишем теперь выражения для полного давления вещества
и излучения
Рассмотрим модель звезды, в которой связь между плотностью и температурой дается
формулой
где
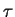
-- постоянный множитель. Тогда давление вещества
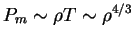
и давление излучения
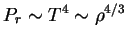
, т.е. в такой модели
отношение давления излучения и вещества постоянно по звезде и
Отметим, что в этом случае энтропия
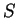
меняется (Как? Растет или падает наружу?).
Введем величину
тогда
Параметр
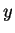
имеет простой смысл:
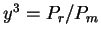
.
Таким образом,
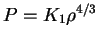 , и мы имеем уже знакомое нам уравнение политропы
, и мы имеем уже знакомое нам уравнение политропы
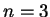 . Мы знаем, что в этом случае равновесие возможно только при одном значении
массы. Подставляя
. Мы знаем, что в этом случае равновесие возможно только при одном значении
массы. Подставляя 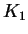 в формулу (2.1), получим
в формулу (2.1), получим
Используя эту формулу, можно оценить роль давления излучения для звезды данной массы
(см. табл. 2, в которой принято
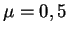
).
Таблица 2.2:
Рост давления в зависимости от массы звезды (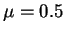 )
)
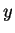 |
0.05 |
0.1 |
0.7 |
1 |
2 |
10 |
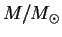 |
0.85 |
2.4 |
70 |
215 |
5800 |
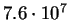 |
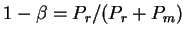 |
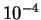 |
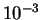 |
0.25 |
0.5 |
0.89 |
0.999 |
Из таблицы 2 видно, что звезда с массой
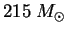 является граничной (
является граничной (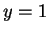 ).
Как показал А.Эддингтон, для звезд с массой порядка
).
Как показал А.Эддингтон, для звезд с массой порядка
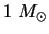 роль давления
излучения пренебрежима, а для звезд с
роль давления
излучения пренебрежима, а для звезд с
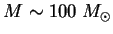 давление излучения
является доминирующим.
давление излучения
является доминирующим.
Применим теорему вириала к построенной выше модели. С учетом излучения тепловая
энергия звезды
По теореме вириала гравитационная энергия звезды
Полная энергия звезды
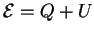
т.е. звезда гравитационно связана, но эта связь равна только той доле энергии,
которая определяется веществом
поэтому при
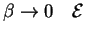
-- мало. В этой модели мы искусственно ввели
политропу
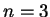
, но энтропия не постоянна по звезде (если
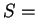
const по звезде,
то при
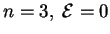
). Подчеркнем разницу между показателем адиабаты
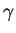
и показателем политропы
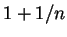
. Возьмем одноатомный нерелятивистский газ (
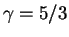
), для которого
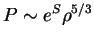
. Пусть распределение энтропии по звезде
определяется зависимостью
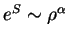
, тогда давление и плотность связаны
соотношением
Структура звезды будет определятся показателем политропы (здесь
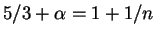
),
а устойчивость зависит от показателя адиабаты, т.е. от упругости вещества (в нашей
модели
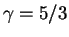
).
За счет распределения энтропии мы можем получить устойчивую звезду, например, с
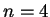 . В рассматриваемой выше модели
. В рассматриваемой выше модели 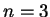 , но полная энергия этой звезды не
равнялась нулю, так как модель неизэнтропична. Устойчивость звезды определяется
не распределением вещества, а тем, как оно ведет себя при сжатии (т.е. его упругостью!).
, но полная энергия этой звезды не
равнялась нулю, так как модель неизэнтропична. Устойчивость звезды определяется
не распределением вещества, а тем, как оно ведет себя при сжатии (т.е. его упругостью!).
<< 2.4 Теория белых карликов
| Оглавление |
3. Перенос излучения в звездах >>
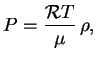
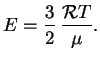
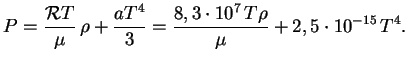
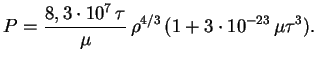
![]() , и мы имеем уже знакомое нам уравнение политропы
, и мы имеем уже знакомое нам уравнение политропы
![]() . Мы знаем, что в этом случае равновесие возможно только при одном значении
массы. Подставляя
. Мы знаем, что в этом случае равновесие возможно только при одном значении
массы. Подставляя ![]() в формулу (2.1), получим
в формулу (2.1), получим
![]() является граничной (
является граничной (![]() ).
Как показал А.Эддингтон, для звезд с массой порядка
).
Как показал А.Эддингтон, для звезд с массой порядка
![]() роль давления
излучения пренебрежима, а для звезд с
роль давления
излучения пренебрежима, а для звезд с
![]() давление излучения
является доминирующим.
давление излучения
является доминирующим.
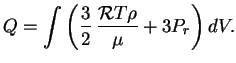
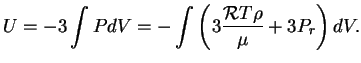
![]()
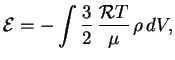
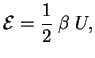
![]() . В рассматриваемой выше модели
. В рассматриваемой выше модели ![]() , но полная энергия этой звезды не
равнялась нулю, так как модель неизэнтропична. Устойчивость звезды определяется
не распределением вещества, а тем, как оно ведет себя при сжатии (т.е. его упругостью!).
, но полная энергия этой звезды не
равнялась нулю, так как модель неизэнтропична. Устойчивость звезды определяется
не распределением вещества, а тем, как оно ведет себя при сжатии (т.е. его упругостью!).