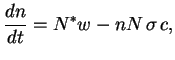<< 3.2 Основные понятия ... | Оглавление | 3.4 Тормозное излучение зарядов >>
3.3 Кинетика фотонов и формула Планка
Рассмотрим теперь, как меняется функция распределения фотонов с учетом их взаимодействия
с веществом. Пусть имеется среда из атомов, которые могут находиться только в
двух состояниях -- в основном и возбужденном, и разность между этими уровнями
равна ![]() , и пусть имеется
, и пусть имеется ![]() атомов/
см
атомов/
см![]() в основном состоянии и
в основном состоянии и
![]() -- в возбужденном. Тогда кинетическое уравнение для числа заполнения можно
записать в виде
-- в возбужденном. Тогда кинетическое уравнение для числа заполнения можно
записать в виде
где первый член в правой части учитывает увеличение числа квантов в результате их испускания возбужденными атомами с вероятностью
![$\displaystyle {dn\over {dt}}=w[N^*(1+n)-Nn]=w[N^*-n(N-N^*)].
$](https://images.astronet.ru/pubd/2008/02/15/0001226214/img614.gif)
В условиях локального термодинамического равновесия, которое осуществляется внутри звезд, ничего подобного быть не может, так как распределение атомов по энергиям описывается формулой Больцмана:
![$\displaystyle {dn\over {dt}}=w N[e^{-h\nu/kT}-n(1-e^{-h\nu/kT})].
$](https://images.astronet.ru/pubd/2008/02/15/0001226214/img618.gif)
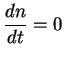 и
и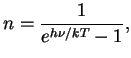
Легко убедиться, что равновесие устойчиво. Запишем уравнение кинетики в виде
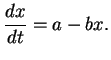
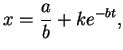
Рассмотрим предельные случаи формулы Планка.
1. Рэлей -- Джинсовская область.
![]() . Используя разложение
. Используя разложение
![]() , получим для числа заполнения:
, получим для числа заполнения:
![]() ,
а для интенсивности
,
а для интенсивности
![]() . Как
видим, в последнее выражение постоянная Планка не входит. Формула
. Как
видим, в последнее выражение постоянная Планка не входит. Формула
![]() первоначально была получена в классической теории. Колебания электромагнитного
поля можно представить набором осцилляторов, каждый из которых имеет энергию
первоначально была получена в классической теории. Колебания электромагнитного
поля можно представить набором осцилляторов, каждый из которых имеет энергию ![]() .
Ясно, что формула Рэлея -- Джинса неприменима при малых
.
Ясно, что формула Рэлея -- Джинса неприменима при малых ![]() из-за расходимости
интеграла
из-за расходимости
интеграла
![]() (ультрафиолетовая катастрофа). Кроме того, при
(ультрафиолетовая катастрофа). Кроме того, при
![]() она не согласуется с опытом. Но при
она не согласуется с опытом. Но при ![]() следует использовать другое
предельное разложение формулы Планка.
следует использовать другое
предельное разложение формулы Планка.
2. Виновская область:
![]() . Это распределение
имеет вид формулы Больцмана. Ее мы получили бы, если бы пренебрегли в кинетическом
уравнении индуцированным излучением (так как
. Это распределение
имеет вид формулы Больцмана. Ее мы получили бы, если бы пренебрегли в кинетическом
уравнении индуцированным излучением (так как ![]() ). Точное выражение для
плотности энергии
). Точное выражение для
плотности энергии
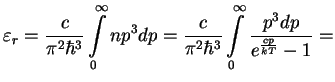
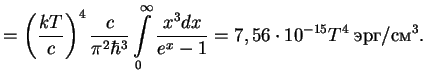
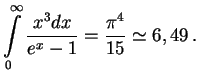
Замечание. Отметим, что формула Вина очень удобна для приближенного
вычисления интегральных величин в теории излучения. Например, при вычислении полной
энергии точное выражение
![]() можно заменить приближенным
интегралом
можно заменить приближенным
интегралом
![]() . В этом случае
. В этом случае
![]() , а интеграл
, а интеграл
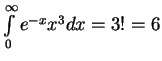 (сравните с точным значением
(сравните с точным значением
![]() ). Виновское
приближение является первым членом в разложении функции Планка:
). Виновское
приближение является первым членом в разложении функции Планка:
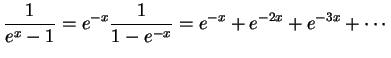
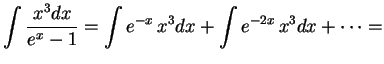
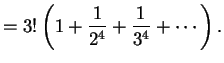
Используя Виновское приближение, легко вычислить, какая доля энергии излучается
в области частот б
![]() льших некоторых. Например,
льших некоторых. Например,
![]() -- 60%
-- 60%
![]() -- 40%
-- 40%
![]() -- 6%.
-- 6%.
Отметим, что несмотря на экспоненциальный множитель существенная доля энергии
(6%) излучается при ![]() .
.
Ранее в кинетическом уравнении
![]() , мы предполагали, что
, мы предполагали, что ![]() -- вероятность перехода с одного
уровня на другой. В действительности уровни имеют некоторую ширину (размыты), и
полная вероятность перехода определяется интегралом (Размерность
-- вероятность перехода с одного
уровня на другой. В действительности уровни имеют некоторую ширину (размыты), и
полная вероятность перехода определяется интегралом (Размерность
![]() с
с![]() в отличие от
в отличие от
![]() см
см![]() с
с![]() .)
.)
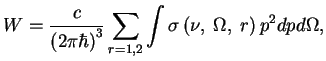
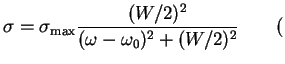 формула
Лоренца
формула
Лоренца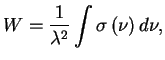
Рассмотрим причины размытости уровней. В нулевом приближении по квантовой теории
возможны только строго определенные энергетические уровни. В следующем приближении
появляется возможность переходов между энергетическими состояниями атома, и в силу
нестационарности состояний уровни энергии оказываются размытыми -- по принципу
неопределенности на величину
![]() . Испускаемые кванты будут иметь
размытость порядка
. Испускаемые кванты будут иметь
размытость порядка ![]() по частоте.
по частоте.
Вероятности распада могут быть разными. Например: переход с уровня ![]() в основное
состояние атома водорода происходит за
в основное
состояние атома водорода происходит за
![]() с, в то время
как в линии в 21 см за
с, в то время
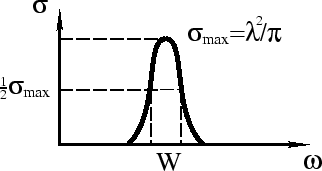
как в линии в 21 см за ![]() лет. Важно, что при этом изменяется только ширина
лет. Важно, что при этом изменяется только ширина
![]() , пропорциональная
, пропорциональная ![]() , но всегда
, но всегда
![]() (рис. 17).
(рис. 17).
Все это верно для одного изолированного атома. В действительности атомы взаимодействуют.
В реальном газе существует ряд причин, по которым спектральные линии расширяются:
столкновения частиц, допплер-эффект, штарк-эффект. При этом может случиться, что
![]() окажется меньше. Например, из-за допплер-эффекта должен сохраняться
интеграл
окажется меньше. Например, из-за допплер-эффекта должен сохраняться
интеграл
![]() и
и
![]() снижается.
снижается.
Следует помнить, что естественная высота сечения
![]() сохраняется, если нет размывающих его механизмов. В качестве примера можно рассмотреть
эффект Мессбауэра. Если принять соответствующие меры (грубо говоря, закрепить атомы
в кристаллической решетке), то можно наблюдать резонансные линии
сохраняется, если нет размывающих его механизмов. В качестве примера можно рассмотреть
эффект Мессбауэра. Если принять соответствующие меры (грубо говоря, закрепить атомы
в кристаллической решетке), то можно наблюдать резонансные линии ![]() -излучения
ядер, при этом сечение как раз равно
-излучения
ядер, при этом сечение как раз равно
![]() .
.
<< 3.2 Основные понятия ... | Оглавление | 3.4 Тормозное излучение зарядов >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |