<< 3.1 Введение | Оглавление | 3.3 Кинетика фотонов ... >>
3.2 Основные понятия теории равновесного излучения
Пусть ![]() -- число фотонов в клетке фазового пространства, т.е. число заполнения,
которое безразмерно. Для ``ящика'' данного объема можно говорить о числе состояний.
Если состояний много, то число уровней в объеме
-- число фотонов в клетке фазового пространства, т.е. число заполнения,
которое безразмерно. Для ``ящика'' данного объема можно говорить о числе состояний.
Если состояний много, то число уровней в объеме ![]() и в импульсном объеме
и в импульсном объеме ![]() есть
есть
где коэффициент 2 учитывает два возможных состояния с разными поляризациями.
Известно, что импульс фотона ![]() связан с волновым вектором
связан с волновым вектором ![]() формулой
Де Бройля
формулой
Де Бройля
Подставляя это выражение в формулу (3.1), получим более наглядное выражение для плотности числа фотонов
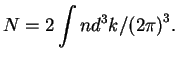
В сферической системе координат
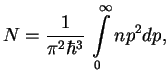
Поскольку энергия одного фотона
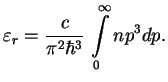
Кроме плотности энергии
![]() важной характеристикой является спектральная
интенсивность излучения
важной характеристикой является спектральная
интенсивность излучения
![]() эрг
эрг![]() см
см![]() с Гц стер
с Гц стер![]() -- величина, которая при отсутствии поглощения или рассеивания не
зависит от расстояния до источника. Из наблюдений всегда получается
-- величина, которая при отсутствии поглощения или рассеивания не
зависит от расстояния до источника. Из наблюдений всегда получается ![]() , а
в физику дела входит число заполнения
, а
в физику дела входит число заполнения ![]() .
.
Получим связь между ![]() и
и ![]() :
:
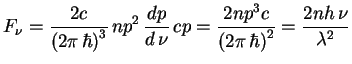
В общем случае (и при отсутствии равновесия) связь между
![]() и
и ![]() дается формулой
дается формулой
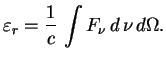
<< 3.1 Введение | Оглавление | 3.3 Кинетика фотонов ... >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |
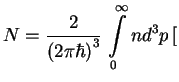 см
см