8.5 Предельный радиус звездных скоплений и устойчивость их корональных областей в поле приливных сил Галактики
Скопления движутся в общем силовом поле Галактики. Так как плотность в них падает с удалением от центра, то при этом непрерывно уменьшается и сила притяжения скоплением звезд, которые являются его членами. На некотором расстоянии от центра скопления сила притяжения звезды скоплением уравновешивается разностью внешних сил притяжения, действующих на звезду и центр масс скопления со стороны галактического центра. Начиная с этого расстояния звезды будут двигаться уже под действием внешних сил, т. е. потеряют связь со скоплением. Это расстояние можно назвать радиусом устойчивости скопления по отношению к приливным силам Галактики, или предельным радиусом скопления.
Пусть скопление с массой ![]() падает по прямой на центр Галактики, где сосредоточена вся ее масса
падает по прямой на центр Галактики, где сосредоточена вся ее масса ![]() . Расстояние между ними обозначим через Rg. Пусть некоторая звезда скопления находится на расстоянии r от его центра на линии, соединяющей центр скопления с центром Галактики, ближе к последнему. Ускорение bg, испытываемое звездой в силовом поле Галактики по направлению к центру Галактики относительно скопления, определяется равенством
. Расстояние между ними обозначим через Rg. Пусть некоторая звезда скопления находится на расстоянии r от его центра на линии, соединяющей центр скопления с центром Галактики, ближе к последнему. Ускорение bg, испытываемое звездой в силовом поле Галактики по направлению к центру Галактики относительно скопления, определяется равенством
|
|
(8.24) |
где G - постоянная тяготения, или, так как Rg 》 r,
|
|
(8.25) |
Ускорение bc, испытываемое звездой по направлению к центру скопления в силовом поле последнего, есть
|
|
(8.26) |
Звезда покидает скопление, если bg > bc. Предельный радиус скопления rs, определяется из условия
|
|
(8.27) |
![$$
r_s = R_g \sqrt[3]{\frac{\mathfrak{M_c}}{2\mathfrak{M_g}}}.
$$](https://images.astronet.ru/pubd/2011/06/28/0001252610/tex/formula251.gif)
|
(8.28) |
Эта формула впервые была получена и опубликована Хёрнером (1957). Для скопления, движущегося по эллиптической орбите с e = 0,5, значение предельного радиуса, согласно Кингу (1962), определяется по формуле
![$$
r_s = R_p \sqrt[3]{\frac{\mathfrak{M_c}}{3,5\mathfrak{M_g}}},
$$](https://images.astronet.ru/pubd/2011/06/28/0001252610/tex/formula252.gif)
|
(8.29) |
где Rp - перигалактическое расстояние скопления.
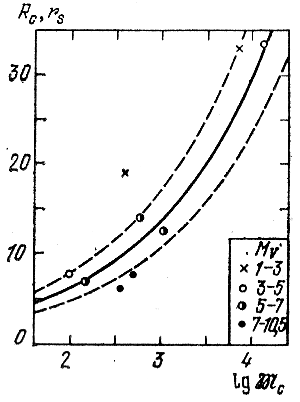
Рис. 127. Зависимость предельных радиусов rs скоплений, находящихся в окрестностях Солнца, от логарифмов масс этих систем (сплошная линия). Rc - наблюдаемые радиусы скоплений.
Для данного шарового скопления величина Rp может быть неизвестна, по мы знаем ее верхний предел, т. е. нынешнее расстояние скопления от центра Галактики. Формула (8.29) показывает, что наблюдаемые размеры скоплений, движущихся по вытянутым орбитам, могут быть существенно меньше предельных размеров, соответствующих их нынешнему расстоянию от галактического центра, хотя бы потому, что при периодическом прохождении через перигалактий внешние разреженные слои скопления будут систематически срываться с него возрастающими приливными силами.
По оценкам Кинга (1962), наблюдаемые радиусы шаровых скоплений М 13 и М 15 в 1,5-2 раза меньше их возможных предельных радиусов. Рассмотрим вопрос о динамической устойчивости корональных областей рассеянных звездных скоплений в поле приливных сил Галактики.
Система, движущаяся по круговой орбите на расстоянии Солнца от центра Галактики, может считаться устойчивой, если ее средняя плотность превышает критическое значение, которое на этом расстоянии для сферических скоплений равно 0, 15 масс Солнца/пс3, а для сфероидальных с предельно малым отношением полуосей 0,6 составляет 0,19 масс Солнца/пс3 (см. § 4.4). Производившиеся до сих пор оценки средней плотности ядер рассеянных скоплений всегда приводили к значениям, значительно превышающим критическое.
С увеличением истинного объема рассеянных скоплений (т. е. с необходимостью учета их корональных областей) средняя плотность этих объектов существенно понижается. Но и в этом случае системы продолжают оставаться устойчивыми в поле приливных сил Галактики.
В самом деле, если принимать за радиусы скоплений радиусы их корональных областей, то средняя плотность скоплений Плеяды и Ясли (единственных наиболее хорошо изученных в интересующем нас аспекте) равна соответственно 0,18 и 0,25 массы Солнца/пс3, т. е., несомненно, превышает критическую.
Для оценки степени устойчивости корон скоплений можно воспользоваться также формулой (8.29). Приняв в данном случае, что Rp = 10 кпс, ![]() = 2 · 1011 масс Солнца, можно вычислить по ней значения предельных радиусов скоплений, находящихся в окрестностях Солнца, в зависимости от логарифмов масс этих скоплений. Эта зависимость изображена на рис. 127 сплошной линией. Прерывистые кривые соответствуют аналогичным зависимостям, построенным в предположении, что масса Галактики вдвое превышает принятое значение (нижняя кривая) или вдвое меньше последнего (верхняя кривая).
= 2 · 1011 масс Солнца, можно вычислить по ней значения предельных радиусов скоплений, находящихся в окрестностях Солнца, в зависимости от логарифмов масс этих скоплений. Эта зависимость изображена на рис. 127 сплошной линией. Прерывистые кривые соответствуют аналогичным зависимостям, построенным в предположении, что масса Галактики вдвое превышает принятое значение (нижняя кривая) или вдвое меньше последнего (верхняя кривая).
Для сравнения этой зависимости с наблюдениями обратимся к табл. 8.1, в которой приведены некоторые характеристики почти всех скоплений, изученных по методике, описанной в двух предыдущих параграфах.
Таблица 8.1
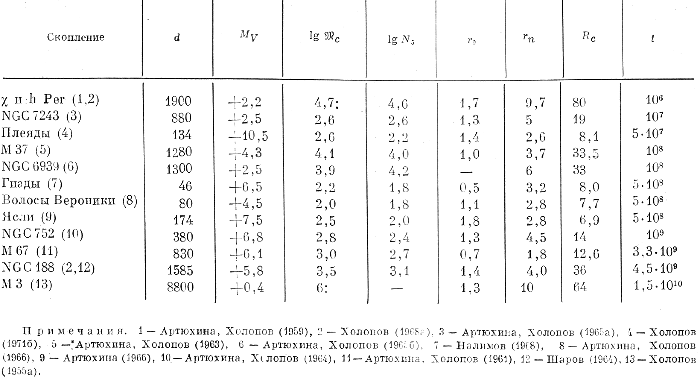
В первом столбце таблицы указано название скопления, сопровождаемое (в скобках) номером примечания к таблице, содержащего ссылку на работу, посвященную исследованию данного скопления. Во втором столбце - выраженное в парсеках расстояние до скопления, принятое для вычисления его размеров. Третий столбец содержит предельную абсолютную величину MV звезд скопления, изученных автором работы, указанной в примечаниях, четвертый - значение нижнего предела логарифма массы скопления (выраженной в единицах массы Солнца), соответствующего величине MV. В пятом столбце дается логарифм числа звезд скопления ярче пятой абсолютной визуальной величины. В ряде случаев значения N5 получены путем экстраполяции известного участка функции светимости скопления. В шестом, седьмом и восьмом столбцах приводятся выраженные в парсеках значения радиусов центральной зоны ядра (r0), ядра (rn) и короны (Rc) скопления. В последнем столбце приведен выраженный в годах приблизительный возраст скопления t, определенный по положению точки поворота главной последовательности. Значения t для М 67 и NGC 188 даны по работе Тварога (1978).
Значения радиусов скоплений Rc как функции логарифмов соответствующих масс ![]() , взятые из табл. 8.1, нанесены на рис. 127 различными символами, зависящими от величины MV, поясненными на рисунке.
, взятые из табл. 8.1, нанесены на рис. 127 различными символами, зависящими от величины MV, поясненными на рисунке.
Рис. 127 свидетельствует о динамической устойчивости корональных областей рассмотренных скоплений. В самом дело, расположение точек на рис. 127 следует форме кривой предельных радиусов. Чем слабее предельная абсолютная величина охваченных подсчетами звезд скоплений, тем ближе к кривой предельных радиусов располагаются соответствующие точки. Наблюдаемые радиусы корон скоплений Плеяды и Ясли определенно меньше возможного предельного радиуса скопления соответствующей массы. Поскольку радиус короны скопления не возрастает существенно с уменьшением светимости его членов (как показано нами на примере ряда богатых скоплений, в том числе и шаровых), с выявлением все более слабых членов (ростом MV) точки на рис. 127 будут. смещаться при этом вправо, и подобно точкам, соответствующим скоплениям Плеяды и Ясли, могут оказаться под кривой предельных радиусов.
Таким образом, можно считать, что корональные области скоплений динамически устойчивы в поле приливных сил Галактики. Они образованы постоянными членами скоплений, движущимися вокруг центров масс последних, а не звездами, покидающими скопления со скоростями, превышающими скорость отрыва.
Конечно, за пределами устойчивых корон должно наблюдаться некоторое количество звезд, действительно покинувших скопление и удаляющихся от него. Эти звезды не должны приниматься во внимание при определении истинных размеров скопления. Выявление их возможно в настоящее время только путем анализа собственных движений звезд в самых широких окрестностях наиболее близких к Солнцу скоплений.
Динамическая устойчивость системы "ядро - корона" в целом свидетельствует о том, что корона является столь же неотъемлемой структурной особенностью любого скопления, как и его ядро. С этой точки зрения мы можем говорить о единстве строения всех звездных скоплений, которое становится особенно очевидным при сопоставлении между собой кривых распределения пространственной звездной плотности в различных системах.
<< 8.4 Ядра и короны - основные области звездных скоплений | Оглавление | 8.6 Единство строения звездных скоплений. Логарифмический диапазон плотностей >>
|
Публикации с ключевыми словами:
звезды - Скопление
Публикации со словами: звезды - Скопление | |
См. также:
Все публикации на ту же тему >> | |