8.4 Ядра и короны - основные области звездных скоплений
В конце десятых годов нашего века Шепли и Трюмплер заметили, что размеры рассеянных звездных скоплений значительно превышают те, которые получаются непосредственно путем простых глазомерных оценок.
Еще в 1916 г. Шепли (1916) нашел, что плотность звездного фона в районе скопления М 67 выше, чем в более далеких его окрестностях. Несколько позже это явление было обнаружено при исследовании скоплений M 11, М 37 и получило название "плечевого эффекта" (Шепли, 1930). Шепли считал, что плечевой эффект - явление довольно обычное для рассеянных скоплений, и усматривал сходство между ним и явлением роста угловых размеров шаровых скоплений по мере перехода к более слабым звездам.
В свою очередь Трюмплер (1918; 1922) на основании подсчетов звезд, проведенных в 1918 г. по данным каталога Боннского обозрения неба (BD) в окрестностях скоплений NGC 752, NGC 6633, Mel 179, Mel 210, Плеяд и Яслей, заключил, что вокруг сильно концентрированных центральных частей этих скоплений, по-видимому, имеются области, содержащие члены скоплений. Эти области обычно не замечаются с первого взгляда, так как число членов скоплений в них мало по сравнению с числом звезд фона. Однако Трюмплер понимал, что, поскольку площадь этих областей велика, в них содержится значительное число членов скоплений, "составляющее в некоторых случаях треть или еще большую долю общего числа". Как и Шепли, Трюмплер подчеркивал, что, по-видимому, этот вывод справедлив для большинства скоплений.
Вскоре Шепли и Сойер (1927в) пришли к выводу, что такие скопления, как NGC 6231, а также χ и h Персея, представляются ядерными конденсациями в гораздо более обширных системах. Тогда же ими была высказана идея, что скопление М 11 может быть ядром звездного облака в созвездии Щита.
В том же году Клейн-Вассинк (1927), определив собственные движения звезд в окрестностях скопления Ясли, показал, что возможные члены скопления встречаются на расстояниях до 2°; ,5 от его центра, в несколько раз превышающих значение видимого радиуса системы. Этот результат позже был подтвержден Хекманом и Крузе (1947).
Несмотря на определенность приведенных выше высказываний Шепли и Трюмплера, факт наличия членов скоплений за пределами видимых очертаний этих систем довольно долго не привлекал особого внимания. По-видимому, считалось, что эти звезды появились вследствие диссипации скоплений, потеряли связь с последними и могут не учитываться при описании характерных особенностей звездных скоплений.
Во всяком случае, исходя именно из таких представлений о роли возможных членов скоплений, находящихся зa пределами видимых очертаний последних, мы решили попытаться выяснить, как распределяются вокруг скоплений покидающие их звезды. Если бы физическая связь таких звезд со скоплением была утрачена, то следовало бы ожидать, что они распределены в некотором вытянутом объеме, ориентированном определенным образом по отношению к галактической орбите скопления. Однако уже первые результаты подсчетов показали, что мы столкнулись с гораздо более широким и интересным кругом явлений.
Цикл работ но анализу распределения звездной плотности в широких окрестностях звездных скоплений (вначале шаровых, а затем, по инициативе Н. М. Артюхиной, и рассеянных) был начат нами в 1954 г. Большинство этих работ выполнено совместно с Н. М. Артюхиной.
В результате мы не только подтвердили заключения Шепли и Трюмплера о существовании вокруг звездных скоплений внешних протяженных областей, которые можно назвать корональными, но и пришли к выводу о том, что эти области являются весьма существенной структурной особенностью звездных скоплений (Холопов, 1955а; 1965б; 1968а; Артюхина, Холопов, 1961; 1963; 1966). Особенно большое значение для обоснования этого вывода имеют выполненные Артюхиной (1966; 1968; 1970; 1972) определения собственных движений звезд в широких окрестностях скоплений Ясли, Плеяды, М 39 и α Персея.
Лишь одно скопление, Гиады, с момента выделения его членов и публикации Л. Боссом (1908) карты, показывающей распределение их на небе (см. рис. 5), являло взору исследователей картину истинной структуры любого сформировавшегося рассеянного скопления. Но еще очень долго звезды корональной области этого скопления относились к потоку Тельца, а название Гиады сохранялось лишь за наиболее плотной центральной областью системы (см.. § 1.6). Впервые, пожалуй, только ван Бурен (1952) изучил структуру Гиад, опубликовав кривые распределения звездной плотности в этой системе.
Любое сформировавшееся скопление (структуру возникающих скоплений мы рассмотрим в гл. 12) состоит из двух основных областей - ядра и короны. Ядро - это наиболее плотная центральная часть системы, то, что непосредственно бросается в глаза как звездное скопление. Корона - это внешняя протяженная, менее плотная область скопления.
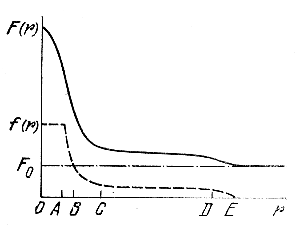
Рис. 123. Схема, поясняющая принцип выделения ядра и короны скопления.
Рис. 123 схематически поясняет эти понятия. Сплошной линией изображено среднее радиальное распределение видимой звездной плотности F(r) в районе сравнительно небогатого звездного скопления (F0 - плотность фона); прерывистая линия представляет соответствующее распределение пространственной плотности звезд в скоплении f(r); Е - граница скопления; С - граница ядра; ОС - область ядра; СЕ - область короны; А - граница центральной зоны ядра, т. е. наиболее плотной центральной зоны скопления, пространственная плотность звезд в которой может считаться практически постоянной; АВ - зона максимального градиента пространственной плотности.
Точки А и D соответствуют точкам перегиба на кривой F(r). Вообще говоря, с приближением к центру скопления градиент функции F(r) может начать уменьшаться лишь в том месте, где f(r) перестает возрастать, т. е. там, где мы вступаем в зону постоянной пространственной плотности. Пространственная плотность в короне может, строго говоря, убывать с удалением от центра системы, но ее градиент обычно очень мал по сравнению с градиентом плотности в ядре (не считая центральной зоны ядра).
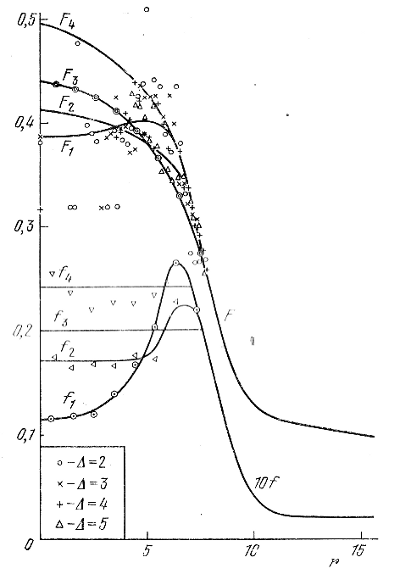
Рис. 124. Изменение вида кривой f(r) в зависимости от хода кривой F(r) в ядре скопления М 37 (Артюхина, Холопов, 1958).
Имея это в виду, мы можем говорить о практичеcком постоянстве пространственной звездной плоскости в объеме короны (в зоне СD). Наличие в центрах скоплений зоны постоянной плотности f(r) можно продемонстрировать на примере скопления М 37 (Артюхина, Холопов, 1958). На рис. 124 показано, как меняется вид кривой f(r) в центральной области скопления в зависимости от вида кривой F(r)). Соответствующие друг другу кривые f и F отмечены одинаковыми индексами. Различными символами на рисунке изображены значения F(r) для подсистемы звезд верхней части главной последовательности скопления (ярче 13m,5 vis), полученные в кольцах разной ширины Δ .
Кривая f1 показывает быстрый рост плотности с удалением от центра до r = 6,5. Совершенно очевидно, что подобный ход кривой f(r), означающий наличие в скоплении центрального объема с пониженной звездной плотностью, объясняется неправильным проведением кривой F1. Если провести кривую видимой плотности F4 так, чтобы она в центральной части располагалась даже выше всех точек, соответствующих наблюдениям, то мы получим кривую f4, по-прежнему свидетельствующую о наличии в центре скопления зоны постоянной плотности.
Таким образом, представление о наличии в центрах скоплений небольшого объема, плотность в котором можно приблизительно считать постоянной, вытекает из наблюдений. Радиус этой зоны r0 не зависит от массы и возраста скопления и для изученных нами систем равен 1 ± 0,8 пс (см. далее табл. 8.1). Так как члены скопления, двигаясь по своим орбитам вокруг центра скопления, являющегося центром его масс, могут удаляться и приближаться к центру, то с течением времени центральная зона ядра в данном скоплении может изменять свои размеры и, может быть, даже "пульсировать". Размеры и центры этих зон для разных подсистем звезд в одном и том же скоплении могут несколько различаться.
У подавляющего большинства (особенно бедных и далеких) скоплений мы до сих пор вообще знаем (видим) только их ядра, так как короны теряются на богатом звездном фоне. На рис. 125, а (Артюхина, 1970) показано распределение видимой плотности звезд ярче 10m,1 в широких окрестностях скопления М 39. Длины черточек соответствуют ожидаемым флуктуациям плотности, определяемым по формуле (8.22). Мы видим, что при проведении обычных подсчетов выявляется лишь ядро этого скопления, проектирующегося на богатый фон Млечного Пути. Но после того как Н. М. Артюхина определила собственные движения всех звезд ярче 12m,2 в области подсчетов и проанализировала распределение плотности только возможных членов скопления, уменьшив тем самым более, чем на порядок, плотность фона и влияние его флуктуации на кривую F(r) звезд скопления, совершенно четко выявилась корональная область скопления, радиус которой по крайней мере втрое превышает радиус ядра системы (рис. 125, б).
Чем меньше звезд в скоплении (или в выделенной и нем звездной подсистеме), тем труднее судить о форме короны. Лишь у очень богатых скоплений можно изучать распределение F(r) в разных направлениях от центра до самых границ системы. В случае бедных систем приходится ограничиваться анализом среднего распределения F(r).
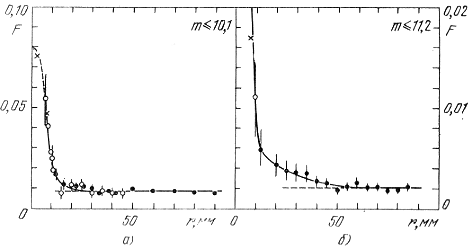
Рис. 125. а - распределение видимой плотности звезд ярче 10m,1 в широких окрестностях скопления М 39; б - распределение видимой плотности возможных членов скопления М 39, выделенных на основании общности их собственных движений (Артюхина, 1970).
С другой стороны, чем богаче скопление, тем труднее, на первый взгляд, оказывается определить границу его ядра. Простая схема, представленная на рис. 123, очень хорошо отражает распределение плотности в скоплениях, состоящих из нескольких десятков или сотен звезд. В более богатых скоплениях между ядром и короной обычно наблюдаются промежуточные зоны, проявляющиеся в виде волн на кривой F(r) или в виде ступенек на кривой f.
На рис. 126 (Холопов, 1963) показаны кривые lgf ярких звезд шаровых скоплений М2, М3 и М15, произвольно смещенные по оси ординат для наилучшего выявления различий их формы. В скобках приведены классы концентрации этих систем. Наиболее плавно плотность меняется у скопления М 2. С ростом класса концентрации, как нам кажется, становятся все более заметными крупномасштабные колебания плотности вне ядер скоплений. Но не будем спешить с заключениями (см. конец § 8.8). Отметим, что эти колебания - не случайные флуктуации: в скоплении М 3 (Холопов, 1953г) резкие изменения градиентов плотности происходят на одних и тех же расстояниях от центра скопления, независимо от того, какая из четырех подсистем ярких звезд скопления рассматривается нами.
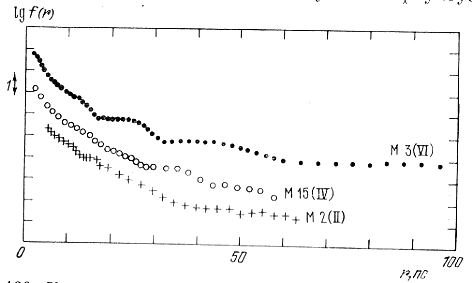
Рис. 126. Кривые lg f(r) ярких звезд шаровых скоплений М 2, М 3 и М 15 (Холопов, 1963); каждое деление на оси ординат соответствует изменению lg f(r) на 1.
Иногда граница между ядром и короной незаметна, и градиент плотности меняется плавно. У подсистем ярких звезд шаровых скоплений градиент функции f(r) с переходом от самых внешних областей к центру может возрастать на шесть порядков, а у бедных звездами рассеянных скоплений - на 1-2 порядка.
Как показывает опыт, с удалением от центра богатого скопления первое резкое уменьшение градиента пространственной плотности происходит в точке, соответствующей радиусу группы звезд, непосредственно наблюдаемой как скопление. Поскольку в случае бедных скоплений мы принимаем эту точку за границу ядра скопления, естественно распространить это определение границы ядра и на случай богатых скоплений. Таким образом, если в бога- том скоплении наблюдается одна или несколько промежуточных зон, условимся считать границей ядра внутреннюю границу ближайшей к центру промежуточной зоны; если градиент плотности меняется плавно, граница ядра не может быть точно определена.
<< 8.3 Методика построения кривых изменения видимой плотности F(r) | Оглавление | 8.5 Предельный радиус звездных скоплений и устойчивость их корональных областей в поле приливных сил Галактики >>
|
Публикации с ключевыми словами:
звезды - Скопление
Публикации со словами: звезды - Скопление | |
См. также:
Все публикации на ту же тему >> | |