Астронет > Звездные скопления

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Звездные скопления << 8.2 Аналитические и численные методы анализа радиального распределения пространственной звездной плотности в скоплениях | Оглавление | 8.4 Ядра и короны - основные области звездных скоплений >>

8.3 Методика построения кривых изменения видимой плотности F(r)

Обычно кривую изменения видимой плотности F(r) cтроят следующим образом. Проекция скопления (для простоты будем считать его сферическим) делится концентрическими окружностями на несколько кольцевых поясов, ширина которых выбирается в зависимости от числа рассматриваемых в скоплении звезд. Число звезд n в каждом кольце делится на площадь последнего s. Результаты деления откладываются на графике по оси ординат, причем за абсциссы наносимых точек принимаются радиусы окружностей $\bar r$ , делящих соответствующие кольцевые пояса ни равные по площади части. Череч немногочисленные полученные точки проводится от руки сглаженная кривая, принимаемая за кривую F(r). Поскольку естественные флуктуации чисел п при случайном распределении звезд в пределах каждого кольца составляют ± $\sqrt n$ , флуктуации Δ F плотности F(r) в каждой точке достигают ± $\frac{\sqrt n}{s}$ , т. е.

$\Delta F = \pm \frac{F(r)}{\sqrt n},$ (8.22)

где n - число звезд, использованное для определения данного значения средней плотности F(r).

При таком способе построения кривой F(r) положения точек, а следовательно, и форма проводимой по ним кривой, зависят от ширины и границ избранных кольцевых зон. Чтобы избежать этой зависимости и получить более объективную кривую F(r), следует производить подсчеты звезд в зонах различной ширины Δ, нанося на один график все получаемые точки разными значками к зависимости от ширины зоны. Кроме того, можно увеличить число точек, последовательно смещая по r границы кольцевых зон.

Таким образом, для каждой выбранной ширины кольцевых зон получали целая серия зон, перекрывающихся так, чтобы соответствующие им точки, по возможности равномерно распределяясь вдоль кривой F(r), фактически обрисовывали ее.

Через полученную совокупность точек проводится по возможности близкая к этим точкам плавная кривая. При этом, когда с удалением от центра скопления возрастает рассеяние точек, соответствующих менее широким зонам, ход кривой определяется точками, полученными с более широкими зонами. Это позволяет уменьшить влияние флуктуации.

Для иллюстрации на рис. 120 (Холопов, 1953в) показана кривая распределения видимой (F) плотности 136 переменных звезд типа RR Лиры в скоплении ω Сеn, построенная таким образом в предположении, что их распределение является сферическим. На том же рисунке показана кривая распределения пространственной плотности (f) этих переменных, полученная из кривой F аналитическим цейпелевским (кружки с точками) и нашим численным (крестики) методами. Радиус скопления принят равным 25', единица длины равна 1'. Согласие результатов, полученных обоими методами, превосходно.

Если бы кривая F(r) не была "материализована" большим числом точек, а ее пришлось бы проводить, как это делают многие, всего лишь через несколько точек, такие детали кривой f(r), как резкое изменение градиента плотности в районах r ≈ 6 и 16,5 были бы потеряны. Даже через точки F(r), изображенные на рис. 120, мы уверены, большинство исследователей провели бы плавную кривую, не поверив в реальность волнообразных изменений плотности в районе 14 < r < 25.

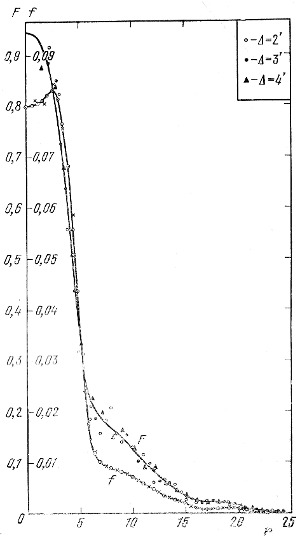
Рис. 120. Кривые видимого (F) и пространственного (f) распределения переменных типа RR Лиры в скоплении ω Сеn (Δ - ширина кольцевой зоны). Кривая F преобразована в кривую f методом Цейпеля и точным численным методом.

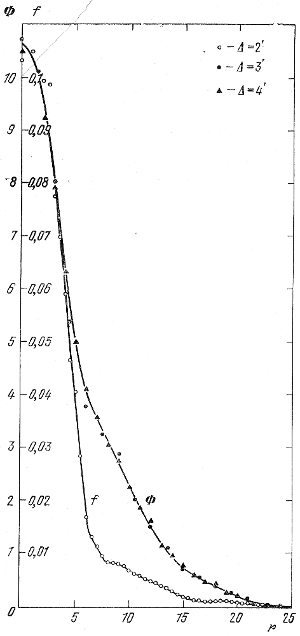
Рис. 121. Кривые Ф(r) и f(r) распределения переменных типа RR Лиры в скоплении ω Сеn (Δ - ширина полосы), полученные по методу Пламмера.

Для контроля правильности нашей интерпретации наблюдаемого хода кривой F(r) мы получили ту же кривую f(r) методом Пламмера. Каждая серия перекрывающихся полос данной ширины последовательно поворачивалась через каждые 15°; на 180°; . Результаты последовательных подсчетов соответствующим образом усреднялись. Полученные таким образом кривые Ф(r) и f(r) изображены на рис. 121 ( Δ - ширина полосы). Мы видим, что при совершенно разном характере кривых F и Ф на рис. 120 и 121, при совершенно разных методах анализа, полученные кривые f(r) в районе 9 < r < 25 на этих рисунках прекрасно согласуются между собой, чего не было бы, если бы кривая F(r) на рис. 120 была проведена иначе. Лишь в районе 6-8' от центра и в самом центре наблюдаются заметные расхождения. Почему?

Центральные плотности более надежно определяются по методу Пламмера, ибо в данном случае в их определении участвует наибольшее число звезд n, а ошибки кривых F(r)) в центральных областях максимальны, ибо с уменьшением r уменьшаются s и n и возрастают значения Δ F, определяемые соотношением (8.22).

Что же касается расхождений в районе 6 < r < 8, то обратим внимание на то, что в этом районе происходит очень быстрое изменение градиентов как функции F(r), так и функции Ф(r). Именно в этом случае выступает на сцену допускаемая почти всеми исследователями при построении кривых F(r)) и Ф(r)) ошибка, условно названная нами ошибкой интервала. Эта ошибка связана с неверным нанесением на график значений F и Ф, получаемых из подсчетов звезд в кольцах и полосах данной ширины Δ.

Как уже отмечалось, обычно значения F(r), вычисляемые для данной кольцевой зоны, относят к расстоянию r, равному квадратному корню из полусуммы квадратов радиусов окружностей, ограничивающих зону. В действительности же их нужно относить к расстояниям r_c, получаемым из соотношения

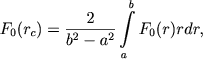
$F_0(r_c) = \frac{2}{b^2 - a^2}\int\limits_a^b F_0(r)rdr,$ (8.23)

где a и b - соответственно радиусы внутренней и внешней окружностей, ограничивающих зону, a F₀(r) - истинная кривая распределения видимой плотности, первым приближением к которой является построенная на рис. 120 кривая F(r).

Разность $\bar r$ - r_c и представляет собой ошибку интервала. Она тем больше, чем больше ширина кольцевой зоны Δ = b - а, и достигает особенно больших значений, когда $\frac{dF}{dr}$ в пределах зоны претерпевает быстрое монотонное изменение.

Для учета ошибки интервала нужно определить значения r_c для всех кольцевых зон, используемых при построении кривой F(r). Первым приближением к кривой F₀(r) является кривая F( $\bar r$ ), построенная при принятии за абсциссы наносимых точек значений $\bar r$ . С этой кривой через равные промежутки r, достаточно малые для выполнения операции численного интегрирования, снимается ряд последовательных значений F(r), охватывающий почти всю кривую. Затем для ряда использованных кольцевых зон данной ширины, равномерно распределенных по области скопления, вычисляются по формуле (8.23), где вместо F₀(r) берется F( $\bar r$ ), значения средних плотностей, по которым с кривой F( $\bar r$ ) снимаются значения r_c первого приближения. Разности r_c - $\bar r$ откладываются на графике против соответствующих значений $\bar r$ . Через полученные точки проводится плавная кривая. Подобные кривые строятся для всех Δ и используются для перехода от абсцисс $\bar r$ к абсциссам r_c.

С полученными значениями r_c строится второе приближение кривой видимой плотности, которое можно принять за окончательное, F₀(r_c), ибо при повторении операции значения гс практически не меняются. Учет ошибки интервала сводит вместе точки, полученные по кольцевым зонам разной ширины и, что самое главное, позволяет обнаружить реальный ход кривой F(r) в области быстрого изменения $\frac{dF}{dr}$ .

В случае эллиптических кольцевых зон вместо радиусов берутся большие полуоси эллипсов $\bar l$ , l_c. На рис. 122, а мы приводим кривую F( $\bar l$ ) для системы переменных типа RR Лиры в ω Сеn, соответствующую наблюдаемым параметрам эллиптичности этой системы (η = 0,75, φ = 90°;). На рис. 122, в показаны кривые, полученные для учета ошибки интервала, а на рис. 122, б - окончательная кривая F(l_c), и соответствующая ей кривая f(l_c), найденная по формулам (8.21) при условии, что а = 1 (i = 90°;).

Сравнение рис. 120 и 122 показывает, что, не зная параметров эллиптичности изучаемой системы, нельзя поручиться за правильность деталей получаемой кривой распределения пространственной звездной плотности в системе.

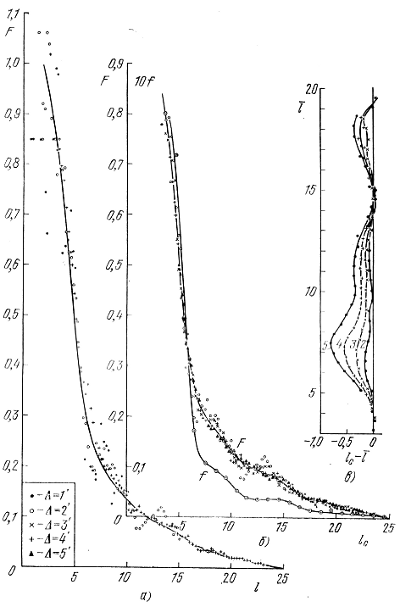
Рис. 122. (а) - предварительная кривая F(l), (б) - окончательная кривая F(l_c) и кривая f(l_c) распределения плотности переменных типа RR Лиры в скоплении ω Сеn (при параметрах эллиптичности η = 0,75, φ = 90°;), (в) - кривые для учета ошибки интервала.

<< 8.2 Аналитические и численные методы анализа радиального распределения пространственной звездной плотности в скоплениях | Оглавление | 8.4 Ядра и короны - основные области звездных скоплений >>

Публикации с ключевыми словами: звезды - Скопление
Публикации со словами: звезды - Скопление

См. также:

Черная дыра разрушает звезду: анимация

Звезды, пыль и туманность в NGC 6559

25 самых ярких звезд на ночном небе

Анимация: черная дыра разрушает звезду

Комета, скопления и туманности

Сравнение размеров звезд

Самая далекая из всех известных звезд?

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце