Звездные скопления << 8.5 Предельный радиус звездных скоплений и устойчивость их корональных областей в поле приливных сил Галактики | Оглавление | 8.7 Процентное содержание звезд разных типов в ядрах и коронах скоплений >>

---

8.6 Единство строения звездных скоплений. Логарифмический диапазон плотностей

Радиус скопления R_c тем больше, чем больше масса скопления (Холопов,1968а). Эта корреляция, неоднократно обнаруживавшаяся ранее для рассеянных скоплений (см., например, Валленквист, 1959), по существу, до недавнего времени относилась лишь к радиусам их ядер. Радиусы скоплений Rc коррелируют также с радиусами их ядер r_n (Холопов, 1968а).

С полной массой скопления явно коррелирует и отношение R_c/r_n. Для скоплений с небольшим числом членов оно близко к 2-3, для более богатых заключено в пределах от 4 до 10. Точно так же коррелирует с массой скопления отношение R_c/r₀, где r₀ - радиус центральной зоны ядра.

Конечно, нельзя ожидать наличия очень тесных связей между всеми рассмотренными величинами, ибо на размеры скоплений, особенно старых, должны, как мы видели, влиять условия их движения в Галактике, сближения с другими объектами, прохождения через более плотные области Галактики и другие факторы. Тем не менее, отмеченные выше корреляции, безусловно, отражают реальность.

Сопоставим теперь между собой радиальные распределения пространственной плотности f(r) в различных скоплениях. Чтобы избавиться от влияния таких факторов как число звезд в скоплении и расстояние его от Солнца, естественно пользоваться логарифмическими шкалами расстояний и плотностей.

Построим диаграммы, на которых по оси абсцисс откладываются значения lg(r/R_c), где r - расстояние от центра скопления, а по оси ординат - значения lg(f(r)/f₀) где f₀ - пространственная звездная плотность в центре скопления. Сведения о характеристиках групп звезд, использованных для построения этих диаграмм (рис. 128 и 129), приводятся в табл. 8.2.

Таблица 8.2

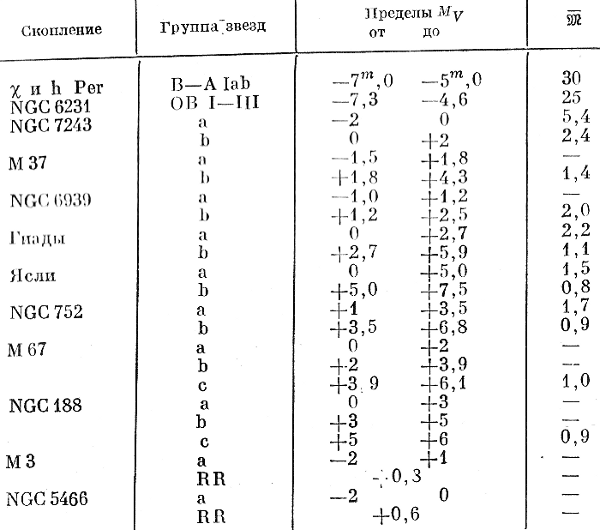
В первом столбце указано название скопления. Для скон-лений, содержащихся в табл. 8.1, использованы работы, перечисленные в примечаниях к этой таблице. Данные, относящиеся к скоплениям NGC 6231 и NGC 5466, а также к подсистемам переменных типа RR Лиры в скоплениях М 3 и NGC 5466, взяты из других наших статей (Холопов, 1962; 1968б). Во втором столбце дается обозначение рассматриваемой группы (подсистемы) звезд. В третьем - пределы абсолютных величин M_V звезд данной группы, и четвертом - их средняя масса , выраженная в единицах массы Солнца.

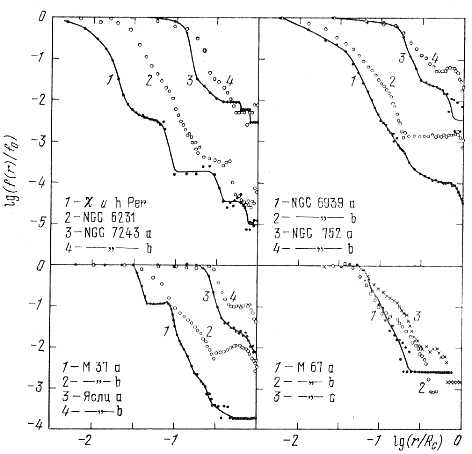
Рис. 128. Зависимости между lg(f(r)/f₀) и lg(r/R_c) для звезд скоплений χ и h Per, NGC 6231, NGC 7243, NGC 752, NGC 6939, M 37, M 67 и Ясли.

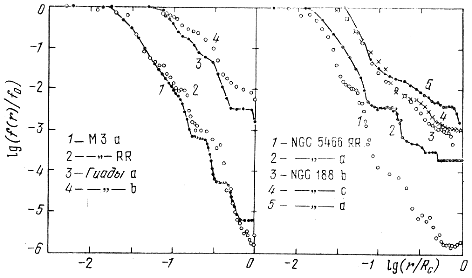
Рис. 129. Зависимости между lg(f(r)/f₀) и lg(r/R_c) для звезд скоплений Гиады, NGC 188, NGC 5466, M 3.

Кривые распределения пространственной плотности звезд разных подсистем в различных скоплениях на рис. 128 и 129 образуют семейства, верхней огибающей которых является горизонтальная прямая lg(f(r)/f₀) = 0, а правой огибающей - вертикальная прямая lg(r/R_c) = 0. Эти кривые показывают, что строение всех скоплений -шаровых и рассеянных, богатых и бедных, старых и недавно сформировавшихся (но не возникающих и не только что возникших!), в сущности, одинаково.

Еще Трюмплер (1922) утверждал, что наиболее важное различие между рассеянными скоплениями заключается в различии их масс, т. е. в различии числа их членов. В структурном отношении это различие действительно играет наиболее важную роль. Собственно говоря, только им определяется исторически сложившееся деление скоплений на шаровые и рассеянные. На диаграммах, представленных па рис.128 и 129, этим различием обусловлена разница расстояний кривых от начала координат. Ближе всех к началу координат расположены кривые, соответствующие скоплениям с небольшим числом членов. По-видимому, подобные диаграммы после надлежащей калибровки можно было бы использовать для определения полных масс скоплений. Поскольку расстояния от начала координат для кривых, соответствующих разным подсистемам звезд в одном и том же скоплении, несколько различаются, более подходящим параметром для этой цели является расстояние от него точки встречи некоторой кривой с осью абсцисс. Эта точка практически одинакова для всех подсистем звезд в данном скоплении. Она соответствует границе центральной зоны ядра, а ее расстояние от начала координат равно величине

(8.30)

Так как отношение R_c/r₀ коррелирует с полной массой скопления, величина D_r действительно в какой-то степени может служить характеристикой полной массы скопления. К сожалению, мы пока не знаем точных значений полных масс скоплений. Вторым параметром, определяющим положение некоторой кривой на рис. 128 и 129, является расстояние от начала координат точки встречи этой кривой c осью ординат. Это расстояние характеризует собой наблюдаемый в данном скоплении логарифмический диапазон пространственной плотности рассматриваемой подсистемы звезд:

(8.31)

Поскольку границу скопления всегда указывают там, где видимая плотность F(r) несколько превышает плотность фона, то и соответствующее значение пространственной плотности f(R_c) отличается от нуля. Было бы бессмысленно считать, что f(R_c) = 0, ибо скопление не имеет резкой границы, а величина D_f при таком определении всегда была бы бесконечно большой. Практически D_f определяется без особого труда с точностью до 0,2-0,4, ибо за f(R_c) можно принимать либо значение постоянной плотности внешней корональной области скопления, либо, если заметное падение f(r) продолжается до самой границы, среднее значение f(r) в этой области. По существу, D_f - это разность логарифмов плотности в центральной зоне ядра и во внешней корональной области скопления.

Величина D_f - хороший показатель степени концентрации звезд к центру системы. В системе с равномерным распределением плотности, - однородной сфере, - D_f = 0. Чем выше степень концентрации звезд к центру системы, тем больше должна быть величина D_f. Вид кривых, соответствующих различным подсистемам, выделенным в данном скоплении, подтверждает это заключение. Чем дальше от центра скопления, тем больше, в среднем, различаются плотности подсистем, имеющих разные значения D_f.

С точки зрения динамики звездных скоплений различие в степени концентрации разных подсистем звезд к центру скопления обычно связывается с различием средних масс звезд этих подсистем. В таком случае можно думать, что D_f также является функцией средней массы звезд данной подсистемы.

Рассмотрим те из кривых, изображенных на рис, 128 и 129, которые соответствуют подсистемам звезд, принадлежащих в основном главной последовательности, т. е. удовлетворяющих обычной зависимости масса - светимость. Только для этих групп звезд в табл. 8.2 приведены значения .

На рис. 130 показана зависимость между lg и D_f, полученная по звездам различных скоплений, возрасты которых заключаются в пределах от 5 · 10⁷ до 10⁹ лет. Для звезд с массами от 0,5 до 3 масс Солнца эту зависимость можно представить в вид

(8.32)

Поскольку числа звезд ярче +5 абсолютной величины в этих скоплениях различаются на два порядка, можно полагать, что даже значительные различия полных масс скоплений не оказывают влияния на значения D_f, и этой зависимостью можно пользоваться для определения средних масс звезд по величине логарифмических диапазонов плотностей подсистем, образуемых ими в скоплениях с возрастом 5 · 10⁸ - 5 · 10⁹ лет.

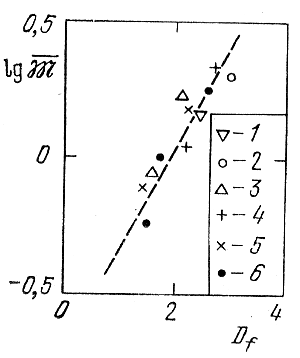
Рис. 130. Зависимость между lg и D_f, полученная по звездам скоплений М 37 (1), NGC 6939 (2), NGC 752 (3), Гиады (4), Ясли (5) и Плеяды (6).

Подсистемы звезд тех же масс в скоплении NGC 7243 (возраст 10⁷ лет) имеют меньшие значения D_f, существенно уклоняющиеся от зависимости (8.32); столь же существенно, но уже в другую сторону, уклоняются от нее значения D_f подсистем звезд главной последовательности скоплений М 67 и NGC 188 (возраст 4 · 10⁹ лет).

С точки зрения динамики звездных скоплений подобные уклонения не являются неожиданными, так как с течением времени центральная плотность ядра скопления должна возрастать, а средняя плотность его стационарной короны вряд ли существенно меняется, поскольку подавляющее число членов скопления с ранних этапов его существования уже находится в короне и может увеличиться лишь за счет немногочисленных звезд, переходящих в область короны из ядра скопления. Поэтому весьма вероятно, что с течением времени будет происходить возрастание величины D_f любой подсистемы звезд в устойчивом звездном скоплении. По-видимому, именно это явление и наблюдается в действительности, ибо возраст NGC 7243 на 1-1,5 порядка меньше, а возраст М 67 и NGC 188 на порядок больше среднего возраста скоплений, определяющих зависимость (8.32).

---

<< 8.5 Предельный радиус звездных скоплений и устойчивость их корональных областей в поле приливных сил Галактики | Оглавление | 8.7 Процентное содержание звезд разных типов в ядрах и коронах скоплений >>

Публикации с ключевыми словами: звезды - Скопление Публикации со словами: звезды - Скопление
См. также: Черная дыра разрушает звезду: анимация Звезды, пыль и туманность в NGC 6559 25 самых ярких звезд на ночном небе Анимация: черная дыра разрушает звезду Комета, скопления и туманности Сравнение размеров звезд Самая далекая из всех известных звезд? Все публикации на ту же тему >>