4.3 Кинематические звездные группы
Новый этап в изучении движущихся звездных групп наступил в 1957 г., когда Эгген (1957; 1958а; 1965в) начал систематическое исследование этих систем. Эгген начал с изучения классических групп Гиад и Сириуса. Принцип, положенный в основу выделения членов группы, является модификацией уже известного метода определения групповых параллаксов. В случае движущегося скопления нам известны собственные движения его членов и точка схождения этих движений. Допустим теперь, что нам хорошо известны расстояние и пространственная скорость некоторой интересующей нас звезды, находящейся в окрестностях Солнца. Это значит, что мы знаем направление и величину вектора скорости звезды. Перенесем его параллельно самому себе в глаз наблюдателя. При продолжении его в бесконечность он пересечет небесную сферу в точке, которую можно назвать апексом данной звезды, по аналогии с апексом Солнца.
Найдем теперь в окружающем нас околосолнечном объеме пространства звезды, которые имеют общее с данной звездой пространственное движение. Эти звезды и образуют движущуюся группу данной звезды. Скоростью группового движения в этом случае служит скорость данной звезды. Слово "движущаяся" уже давно обычно опускается. Точкой схождения собственных движений членов группы служит апекс данной звезды. Таким образом, для того чтобы можно было отнести некоторую звезду к группе данной звезды, нужно, чтобы ее собственное движение μ, и лучевая скорость Vr удовлетворяли определенным требованиям, диктуемым условиями группового движения (см. § 3.3).
Пусть Vr и θ - лучевая скорость и позиционный угол собственного движения некоторой звезды с экваториальными координатами α, δ ; θ (A0, D0) - позиционный угол группового движения в точке (α, δ) небесной сферы, где A0, D0 - экваториальные координаты апекса группы; Vrc - групповая лучевая скорость в точке (α, δ); λ - угловое расстояние звезды от апекса; V - групповая скорость. Тогда Vrc = V cos λ, а значение θ(A0, D0) вычисляется по формуле (3.14). Рассматривая ошибки определения всех этих величин для звезд скопления Гиады, Эгген (1958а) пришел к выводу, что одним из условий для отнеA0, D0, V служит неравенство
|
|
(4.1) |
а другим - неравенство
|
|
(4.2) |
Отобрав таким образом возможные члены группы Гиад, Эгген нашел по методу определения групповых параллаксов их расстояния, а затем - абсолютные величины, после чего построил диаграмму Херцшпрунга - Рессела для членов группы. В состав группы Эгген (1957) включил и скопление Ясли, движущееся в пространстве со скоростью, совпадающей со скоростью Гиад. Впервые обратил на это внимание вместе с Херцшпрунгом еще К. Шварцшильд (1913). В каталоге FK3 оказалось только 20 возможных членов группы Гиад с известными лучевыми скоростями, удовлетворяющих условиям (4.1) и (4.2). Еще четыре прибавилось при введении вместо условия (4.1) требования
|
|
(4.3) |
32 возможных члена группы были выделены Эггеном из числа звезд, находящихся в пределах 20 пс от Солнца, по данным каталога Глизе (1957). На рис. 61 представлена полученная Эггеном (1958а) диаграмма MV, (P - V)E для звезд группы Гиад. Рис. 61, по мнению Эггена, свидетельствует о физической реальности разбросанной по всему небу группы Гиад, ибо диаграммы МV, (Р - V)E для членов группы и членов скоплений Гиады и Ясли в общих чертах сходны, указывая лишь на то, что некоторые члены группы могут быть моложе членов скоплений.
Обращаясь к потоку Большой Медведицы, Эгген (1958а) высказывает мнение, что разреженное "скопление Большой Медведицы является, скорее, местным сгущенном звезд потока, а не его ядром". Впоследствии, правда, Эгген (1965а) признает за скоплением право на существование как самостоятельной части потока. Эгген предпочитает называть этот поток группой Сириуса, опираясь при отборе возможных членов группы не на положение сравнительно плохо определяемого радианта скопления, а на апекс Сириуса. Пользуясь в этом случае критериями
|
|
(4.4) |
|
|
(4.5) |
аналогичными критериям (4.1) и (4.2), Эгген выделяет из числа звезд, рассматривавшихся в работе Роман (1949), 58 возможных членов группы Сириуса, среди которых находятся и яркие члены скопления Большой Медведицы. Диаграмма МV, (Р - V)E, полученная Эггеном (1958а) для звезд этой группы, показана на рис. 62. Крестиками отмечены звезды, которые выпадают из общего хода точек, характеризующих, по мнению Эггена, состав группы. К членам группы Эгген относит звезды, образующие узкую главную последовательность, и компактную группу желтых гигантов с МV ≈ 0 и (Р - V)E ≈ +0m,8. Остальные звезды могут не относиться к группе, случайно двигаясь в направлении ее движения с той же скоростью.
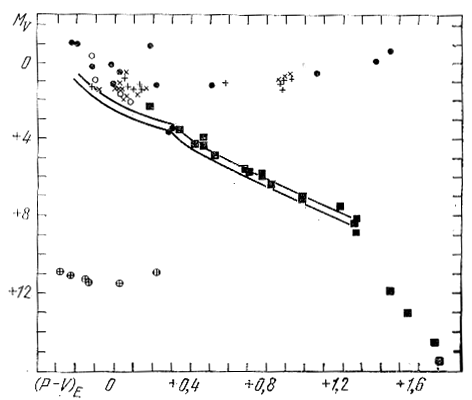
Рис. 61. Диаграмма МV, (Р - V)E членов группы Гиад (Эгген, 1958а). Черные кружки - члены группы, удовлетворяющие условиям (4.1) и (4.2), светлые кружки - условиям (4.3) и (4.2). Крестики и плюсф - ярчайшие члены скопления Гиады и Ясли соответственно. Черные квадраты - возможные члены из числа ближайших звезд. Кружки с крестиками - белые карлики. Двойной линией намечена "стандартная" главная последовательность (Эгген, 1955).
Скорости движения групп Сириуса и Гиад относительно Солнца сравнительно невелики (18,4 и 44,0 км/с соответственно). Исследовав эти группы, Эгген (1958б) обратился к составленному им списку 700 звезд с высокими скоростями с тем, чтобы выявить возможные движущиеся группы среди этих объектов.
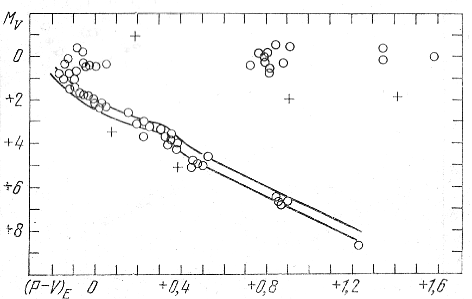
Рис. 62. Диаграмма МV, (Р - V)E членов группы Сириуса (Эгген, 1958а).
Рассмотрев три звезды с большими параллаксами (ζ Her, ε Ind и 61 Cyg), имеющие надежно определенные пространственные скорости относительно Солнца (74,5, 88,5 и 108,0 км/с), Эгген выявил связанные с этими звездами движущиеся звездные группы, состоящие соответственно из 23, 15 и 16 членов. По оценке Эггена, к каждой группе могло быть отнесено не более двух-трех случайно движущихся с ее скоростью звезд поля. Таким образом, группа 61 Cyg вновь возродилась, как Феникс из пепла. На рис. 63 (Эгген, 1958б) представлена диаграмма МV, (Р - V)E членов этих групп, очень похожая на подобную диаграмму членов старого рассеянного скопления М 67 (см. далее рис. 147).
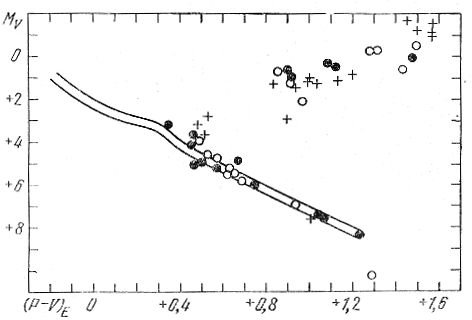
Рис. 63. Диаграмма МV, (Р - V)E для звезд групп ζ Her (крестики), ε Ind (светлые кружки) и 61 Cyg (черные кружки) согласно Эггену (1958б).
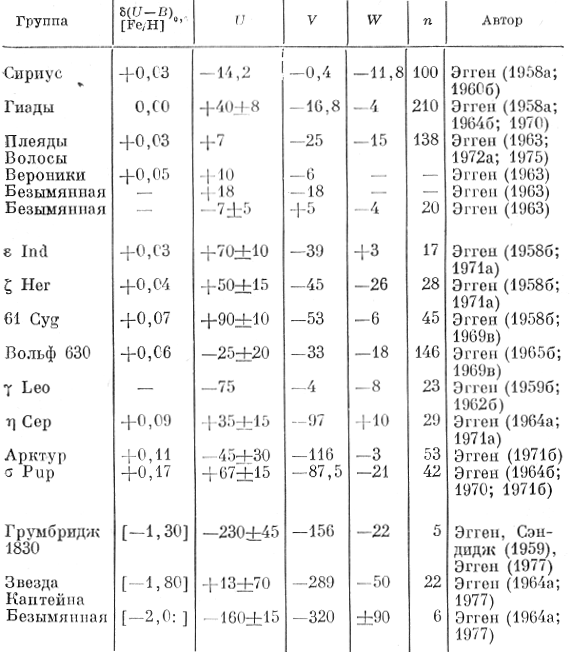
В ряде последующих работ Эгген (1959а, б; 1964а, б; 1965а, б, в) продолжал исследование уже рассмотренных и поиски новых звездных групп, сведения о которых приведены в табл. 4.1. В первом столбце таблицы содержится название группы; во втором - значение ультрафиолетового избытка δ(U - B)0,6 звезд группы (см. § 6.3) или (в квадратных скобках) значение [Fe/H], являющиеся указателями содержания металлов у членов группы - важного дополнительного критерия, используемого для отбора этих членов; в третьем, четвертом и пятом столбцах - выраженные в км/с значения компонентов пространственной скорости членов группы, направленных соответственно от галактического центра в плоскости Галактики (U), в направлении галактического вращения в той же плоскости (V) и к северному полюсу Галактики (W). В шестом столбце приводится число членов группы (n), в седьмом - ссылка на основные работы, посвященные исследованиям группы.
Таблица 4.1
Переход от компонентов пространственных скоростей, выраженных в экваториальной системе координат, к имеющим более ясный физический смысл галактическим компонентам U,V,W, отражающим особенности движениям звезд в пространстве по их галактоцентрическим орбитам, показал, что движения членов групп в направлении, перпендикулярном к галактической плоскости (W), могут быть независимы от U- и V-компонентов их скоростей. Считая, что члены группы имеют общее происхождение, можно допустить, что они сохраняют дисперсию скоростей, присущую им после их образования в некотором первоначальном объеме диффузного облака, обращавшегося вокруг галактического центра. Как отметил Вулли (1961), наблюдатель, регистрирующий в окрестностях Солнца огромную рассеянную группу звезд, имеющих общее происхождение, видит лишь выборку из первоначальной группировки, а именно только те ее члены, которые к моменту наблюдения оказались в том объеме галактического пространства, через который в это время проходит Солнце; звезды, образующие эту выборку, неизбежно должны обладать одинаковым значением компонента V скорости, с которой они обращаются вокруг галактического центра. При этом они могут иметь заметную дисперсию U- и W-компонентов их скоростей, при условии, что в процессе движения они остаются вблизи некоторой средней орбиты начального облака. Дисперсия W-компонентов скоростей членов группы зависит по только от первоначальной дисперсии этих скоростей (обусловливающей различия U-компонентов), по и от размеров начального облака и его положения относительно галактической плоскости.
Исходя из этих соображений, уже с 1960 г. Эгген (1960а) принял следующую процедуру отбора возможных членов группы Гиад. Сначала из списка звезд поля отбираются все звезды с довольно большими значениями разностей θ - θ(А0, D0) и Vr - Vc (см. формулы (4.1) - (4.3)). Для этих звезд с помощью приемлемых значений фотометрических параллаксов, соответствующих спектральным классам звезд, находятся компоненты векторов пространственных скоростей U, V, W. Если для любого из допустимых значений параллакса получающиеся значения U и V совпадают в заданных пределах с принятыми значениями U- и V-компонентов пространственной скорости Гиад, данная звезда выделяется в качестве кандидата в возможные члены группы. Значение компонента W при этом совершенно игнорируется. Затем по обычной формуле (1.1) вычисляется групповой параллакс данной звезды и уточняются значения U-, V-компонентов ее скорости. По значениям MV, найденным с помощью групповых параллаксов, звезды наносятся на диаграмму (MV, показатель цвета), построенную для членов скопления Гиады. Звезда считается членом группы, если она попадает в заданные пределы любой последовательности, наблюдаемой на этой диаграмме.
На построенной Эггеном (1960а) диаграмме МV, (B - V)E членов группы Гиад, выделенных таким образом, обращает на себя внимание возможная принадлежность к этой группе переменной δ Щита, являющейся прототипом соответствующего типа переменных звезд. Группа вытянута в направлении галактического вращения. Половина членов группы - двойные и кратные системы. Между |z|-координатами и значениями |W| звезд группы Гиад существует заметная корреляция. Звезды с большими значениями |z| имеют малые |W|. В дальнейшем они должны начать падать к галактической плоскости с возрастающей скоростью, достигая максимума скорости |W| при пересечении этой плоскости.
При повторном изучении группы Сириуса Эгген (1960б) принял несколько иную процедуру отбора членов группы, чем в случае группы Гиад, поскольку движение по z-координате у Сириуса сравнимо по величине с полной пространственной скоростью группы. Мы опишем эту процедуру, ставшую основной во всех последующих подобных работах Эггена, чтобы показать, к каким ухищрениям приходится прибегать исследователям движущихся групп звезд, отказывающимся от строгих ограничений классического метода групповых параллаксов, накладываемых на пространственные скорости звезд требованием равенства векторов этих скоростей.
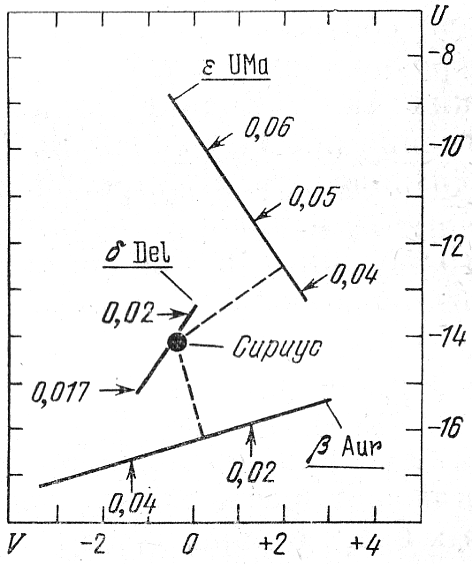
Рис. 64. Часть плоскости (U, V), содержащая Сириус
и три возможных члена его группы (Эгген, 1960б).
В связи с этим, в дальнейшем мы будем называть группы звезд, выделяемые в пространстве скоростей по признаку общности какого-либо из компонентов векторов их скоростей, кинематическими звездными группами, чтобы отличать их от движущихся скоплений и групп, у которых должны быть одинаковы векторы скоростей их членов.
На рис. 64 (Эгген, 1960б) изображена часть плоскости (U, V), содержащая Сириус и три возможных члена его группы - ε UMa, β Aur и δ Del. Стрелками показаны точки, соответствующие различным значениям параллаксов этих звезд, дающим соответствующие значения компонентов U, V их скоростей. В случае движущихся скоплений прямые на плоскости (U, V), соответствующие членам скоплений, должны проходить через одну точку.
За возможные члены группы Сириуса Эгген принимает те звезды, кратчайшие расстояния геометрических мест расположения компонентов U, V которых от точки, соответствующей положению Сириуса, не превышают 4 км/с. Эти расстояния показаны на рис. 64 прерывистыми линиями. Значения параллаксом, соответствующие этим расстояниям, и принимаются Эггеном за значения групповых параллаксов рассматриваемых звезд, не зависящие от значений W-компонеитов их скоростей. Таким путем Эггену удалось причислить к группе Сириуса уже 100 членов, в том числе δ Del, переменную типа δ Щита.
Использование плоскости (U, V) позволяет обнаруживать кинематические группы по местам концентрации на ней соответствующих точек. Практически все группы, перечисленные в табл. 4.1, перешли в разряд кинематических по методике выделения их возможных членов. Именно поэтому значения U, приведенные в этой таблице, для ряда групп сопровождаются указанием пределов возможных различий U-компонентов членов данной группы. Приведенные в той же таблице значения W-компонентов объектов, олицетворяющих кинематические группы, по сути дела для данной группы случайны и для отдельных ее членов могут различаться в очень широких пределах.
Группы в табл. 4.1 расположены в порядке уменьшения содержания металлов и разбиты на три части. Первая включает шесть групп, состоящих из сравнительно молодых звезд с нормальным и высоким содержанием тяжелых элементов и диаграммами MV, В - V, подобными диаграммам Плеяд и Гиад. Эгген относит их к молодому населению диска Галактики. Восемь групп второй части таблицы (с несколько меньшим, в среднем, содержанием металлов) можно отнести к старому населению диска. Диаграммы MV, В - V их членов, как мы уже видели, напоминают диаграммы старых рассеянных скоплений вроде М 67. Наконец, три последние группы, несомненно, относятся к сферической составляющей Галактики, и диаграммы MV, В - V их членов сходны с аналогичными диаграммами звезд шаро-ых скоплений, см. рис. 65 (Эгген, 1977), на котором показаны диаграммы MV, В - V для членов группы звезды Каптейна и для шарового скопления М 3.
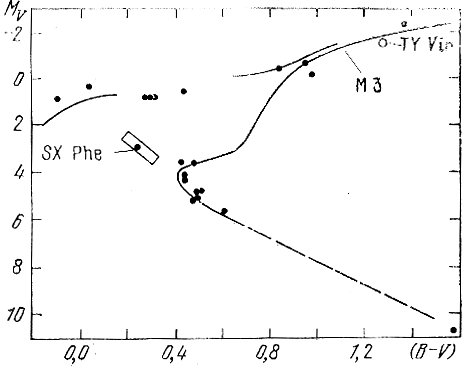
Рис. 65. Диаграмма MV, В - V для членов группы звезды Каптейна (точки) и шарового скопления М 3 (Эгген, 1977).
Мы уже знаем, что в группу Гиад входят два рассеянных скопления - Гиады и Ясли, сходные по возрасту и многим другим физическим характеристикам, скопления-близнецы. К группе Сириуса, содержащей скопление Большой Медведицы, Ллойд Ивэнс и Мидоус (1964) отнесли по кинематическим признакам скопление NGC 7092 (М 39), диаграмма MV, В - V которого совпадает с диаграммой скопления Большой Медведицы. Значения компонентов скоростей U, V и W для скопления NGC 7092 равны соответственно -20 ± 3, +1 ± 3 и -11 ± 3 км/с. Этот вывод подтвердил и Эгген (1965в).
Одновременно и вслед за этим Эгген (1964в; 1965в; 1974) отнес большое число молодых рассеянных скоплений, перечисленных в табл. 4.2, к группе Плеяд. В столбце r табл. 4.2 мы приводим расстояния этих скоплений от Солнца в шкале Эггена, поскольку именно на этих значениях r основаны приведенные в той же таблице величины U, V, W для скоплений этой кинематической группы. Три последних скопления в табл. 4.2 Эгген (1974) считает лишь возможными членами группы.
| Скопление | r(пс) | U | V | W | Автор |
| Плеяды | 129 | +7 | -25 | -15 | Эгген(1964в; 1965в;1974; 1975) |
| α Per | 178 | +14 | -25 | -6 | Эгген(1964в; 1965в;1974а; 1974) |
| NGC 2516 | 445 | +24 | -26 | +7 | Эгген(1964в; 1965в;1974а; 1974) |
| IC 2602 | 151 | +4 | -27 | +3 | Эгген(1964в; 1965в;1974а; 1974) |
| NGC 1039 | 440 | +3 | -27 | -20 | Эгген(1964в) |
| δ Lyr | 316 | +15 | -24 | +1 | Эгген(1968б;1972а; 1974) |
| NGC 2287 | 759 | (+21) | (-26) | (-6) | Эгген(1971г;1972а; 1974) |
| Cr 121 | 500 | (+25) | (-25) | (-15) | Эгген(1974) |
| NGC 6885 | 417 | (+2) | (-25) | (-11) | Эгген(1974) |
Скопления, входящие в группу Плеяд, занимают огромный объем пространства. Если учесть, что часть звезд из группировки Скорпиона - Центавра также причисляется Эггеном (1972а) к группе Плеяд, то станет ясно, что к этой группе Эгген относит очень большую долю молодых скоплений Пояса Гулда, т. е. Местной системы, которую Эгген (1975) называет местной ассоциацией. Эгген вообще допускает возможность того, что "весь комплекс Пояса Гулда возник из одного газового облака, двигавшегося вокруг центра Галактики", и относит к местной ассоциации ряд Т-ассоциаций, наблюдаемых в темных туманностях созвездий Тельца, Хамелеона, Волка. Судя по диаграммам Mbol, lgTe для звезд группы Плеяд, опубликованным Эггеном (1972а; 1975), видно, что в этом случае им допускается заметное различие возрастов членов группы (в пределах от 1 · 107 до 8 · 108 лет).
Многие (см., например, Бенедикт Арнольд, 1974) сомневаются в реальности групп Эггена. Среди множества звезд разного возраста и химического состава, движущихся в окрестностях Солнца в разных направлениях и с разными скоростями, всегда можно подобрать некоторое число объектов, которые будут иметь заданные скорости и окажутся на таких расстояниях от Солнца, что соответствующие им точки расположатся на диаграмме MV, В - V вдоль заданных последовательностей, характер которых нетрудно предвидеть. В связи с этим, следует с большой осторожностью относиться к результатам использования звездных групп для определения светимости редко встречающихся объектов, которые зачисляются в эти группы (обычно, ими оказываются яркие переменные звезды). Мы уже упоминали о нескольких переменных, причисленных к группам Гиад и Сириуса. Эгген относит к группе Плеяд цефеиду α UMi, переменную типа δ Щита DY Peg - к группе σ Pup, a R CrB - к группе Вольф 630. К группе Грумбридж 1830 была отнесена сама RR Lyr, медианная абсолютная величина которой MV при первом определении оказалась равной +0m,6. Позже Эгген (1977) нашел для нее новое значение MV = +0m,35.
Наибольшее число переменных отнесено к группе звезды Каптейна (см. рис. 65): здесь и переменные типа RR Лиры, SU Dra, U Lep, X Ari, ST Leo, медианные абсолютные величины Mv которых, полученные по групповым параллаксам этих звезд, заключены в пределах от +0m,6 до +0m,85, и полупра