3.3 Групповые параллаксы
Групповыми параллаксами называются определяемые с помощью формулы (1.1) индивидуальные параллаксы звезд, входящих в состав движущихся скоплений (см. § 1.6). Как показывает эта формула, точность групповых параллаксов зависит от точности определения лучевых скоростей, собственных движений и координат точки пересечения больших кругов, определяемых этими движениями на небесной сфере. При этом в отношении каждой индивидуальной звезды делается неявное (но, несомненно, существенное) допущение о безусловной принадлежности ее к данному движущемуся звездному скоплению. В каждом конкретном случае это допущение может оказаться неверным.
Для определения координат апекса (или радианта) движущегося скопления можно использовать многочисленные методы, предложенные в звездной астрономии для нахождения апекса движения Солнца или в метеорной астрономии для нахождения радиантов метеорных потоков. Подробное изложение этих методов можно найти в книге Полака (1935).
Рассмотрим разработанный Расмусоном (1911; 1921) метод, основанный на методике Болина (1905). В связи с тем, что в некоторые из формул Расмусона вкрались ошибки, по удивительному стечению обстоятельств частично сохранившиеся и в изложении этого метода Полаком, попробуем воспроизвести эти формулы по возможности без ошибок.
На рис. 12 изображена небесная сфера. Р - полюс экваториальной системы координат; S - звезда; α, δ - ее экваториальные координаты; μ - вектор собственного движения звезды, движущейся по большому кругу, полюс которого - Q; A, D - экваториальные координаты этого полюса; К - апекс движущегося скопления, которому принадлежит звезда S; A0, D0 - координаты апекса; К - угловое расстояние звезды от апекса; q - угол между напр авлением собственного движения звезды и проходящим через нее кругом склонения.
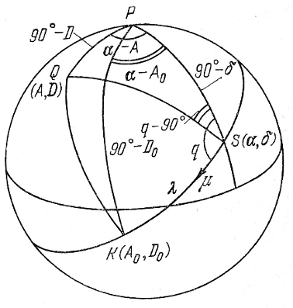
Рис. 12. Схема, поясняющая вывод формул (3.5)-(3.8).
Пользуясь соотношениями μαcos δ = μ sin φ , μδ = μ cos φ , где φ - позиционный угол известного собственного движения звезды, связанный с углом q соотношением q = 360°; - φ (если это движение определено абсолютно точно), μα и μδ - компоненты этого движения по α и δ, из треугольника PQS находим:
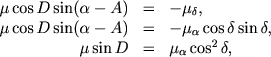
|
(3.5) |
По этим формулам для каждой звезды вычисляются координаты соответствующего полюса A, D.
Рассматривая треугольник QPK, получим соотношение
|
|
(3.6) |
|
|
(3.7) |
Решая по способу наименьших квадратов систему условных уравнений вида (3.6), находим величины х, у, после чего по формулам (3.7) определяются значения A0, D0. Наконец, рассматривая треугольник KPS, нетрудно вывести формулы, позволяющие найти для каждой звезды значения λ и q:
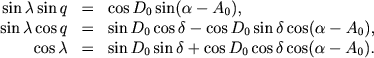
|
(3.8) |
Зная лучевую скорость Vr хотя бы одной звезды движущегося скопления, находим V (пространственную скорость скопления) из соотношения Vr = V cos λ, а затем, по формуле (1.1) , параллакс любой звезды, считающейся его членом.
В методе Болина - Расмусона для нахождения апекса используются только собственные движения звезд. В часто применявшемся для решения той же задачи методе Шарлье (1914) используются также и известные лучевые скорости звезд скопления. Так как метод Шарлье подробно изложен в работах Расмусона (1921) и Полака (1935), мы ограничимся приведением основных его формул. Считая, что пространственные скорости V всех членов скопления одинаковы, можно написать следующие выражения для их компонентов ξ , η ,ζ в прямоугольной экваториальной системе координат (ось ξ направлена в точку весеннего равноденствия, ось η лежит в экваториальной плоскости, ось ζ направлена к северному полюсу мира):
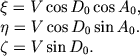
|
(3.9) |
В то же время для каждой звезды скопления выполняется
|
|
(3.10) |
где
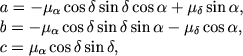
|
(3.11) |
|
|
(3.12) |
причем компоненты собственного движения в (3.11) выражены в радианах. Вычислив для каждой звезды значения a, b, c, находим путем решения по способу наименьших квадратов системы условных уравнений вида (3.10) значения х и y, а затем - координаты апекса А0, D0 из очевидных соотношений
|
|
(3.13) |
Дальнейшие вычисления проводятся так же, как в методе Болина - Расмусона. В сущности, как показал, например, Смарт (1938), основные уравнения методов Болина - Расмусона и Шарлье практически идентичны.
В 1945 г. Сирc (1945) обратил внимание на то, что непосредственное применение формул Шарлье ведет к появлению систематической ошибки в положении апекса, а следовательно, и в определении расстояния до движущегося скопления. Дело в том, что, как видно из уравнений (3.10) и (3.11), коэффициенты нормальных уравнений, составляемых при решении системы условных уравнений (3.10), содержат определяемые из наблюдений величины μα, μδ, искаженные ошибками измерений. Сирc показал, что при этом происходит систематическое преувеличение коэффициентов нормальных уравнений на величины, являющиеся функциями квадратов ошибок измерения значений μα, μδ; соответственно искажается и решение системы нормальных уравнений. Для учета этой ошибки, названной Сирсом ошибкой регрессии, необходимо предварительно исправить коэффициенты нормальных уравнений. Ошибкой регрессии можно пренебречь только в случае очень точных измерений. Аналогичные трудности возникают и в методе Болина - Расмусона, в котором ошибки собственных движений в неявном виде входят в коэффициенты условных уравнений вида (3.6), определяемые с помощью равенств (3.5).
Но этим не исчерпываются недостатки методов Шарлье и Болина - Расмусона. Питри (1949) указал на неустойчивость решений систем уравнений, используемых в этих методах, особенно заметную в тех случаях, когда скопление занимает ограниченную область на небе, а точка схождения собственных движений удалена от него на значительное расстояние. Чтобы справиться с этой трудностью, Питри предложил метод нахождения дифференциальных поправок к предварительно найденным с помощью одного из описанных выше способов координатам апекса, т.е. уточнения положения апекса. Одновременно подобный метод был независимо предложен Роман (1949) и с тех пор успешно используется разными авторами, каждый из которых видоизменяет его в соответствии со своими задачами. Мы рассмотрим его в трактовке Веймана и др. (1965), наиболее близкой к первоначальному изложению Питри, который, по-видимому, не был знаком с работой Сирса (1945) и не подозревал, что его формулы в то же время позволяют избежать ошибки регрессии.
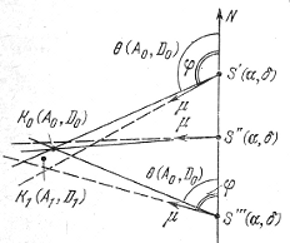
Рис. 13. Схема, поясняющая вывод формул (3.14)-(3.19).
Пусть K1 (A1, D1) на рис. 13 - предварительное положение апекса, К0 (А0, D0) - истинное его положение, являющееся точкой пересечения изображенных прямыми линиями больших кругов, проходящих через каждую из звезд скопления (S', S",...); вдоль этих кругов были бы направлены собственные движения рассматриваемых, звезд, если бы ошибки их определения были равны нулю, а сами звезды двигались в пространстве с равными по величине и параллельными скоростями.
Пусть θ(А0, D0) - позиционные углы упомянутых больших кругов при точках с координатами α , β. Из двух первых формул системы (3.8), учитывая, что q = 2π - θ, находим для определения этих углов соотношение
|
|
(3.14) |
Аналогичное соотношение справедливо для позиционных углов θ(А1, D1) больших кругов, проходящих через точку К1 и точки с координатами α , β:
|
|
(3.15) |
Вычислив по этому соотношению для каждой звезды значения θ(А1, D1), находим для всех звезд значения
|
|
(3.16) |
где φ - позиционные углы наблюдаемых собственных движений этих звезд.
Приняв обозначения ΔА = A0 - A1, ΔD = D0 - D1, можем записать с точностью до членов первого порядка:
|
|
(3.17) |
Так как точка K0 должна быть ближайшей к направлениям собственных движений всех звезд скопления, мы можем отождествить член θ(А0, D0) в соотношении (3.17) с членом φ в соотношении (3.16) и составить ряд условных уравнений
|
|
(3.18) |
которые, учитывая (3.15) и (3.16), можно представить в виде
|
|
(3.19) |
Каждому из условных уравнений следует придать вес в соответствии с вероятной ошибкой εφ угла φ , определяемой из соотношения
|
|
(3.20) |
Решая полученную систему условных уравнений вида (3.19) по способу наименьших квадратов, находим поправки ΔA и ΔD, которые нужно придать к экваториальным координатам A1, D1 предварительного апекса для того, чтобы получить улучшенные координаты апекса A0, D0. Ошибка регрессии в данном случае не возникает, так как коэффициенты условных уравнений (3.19), а значит, и соответствующих им нормальных уравнений являются точными числами.
Существуют и другие методы определения точного положения точки схождения собственных движений звезд скопления, называемой часто вертексом. Как одну из интересных модификаций метода дифференциальных поправок можно упомянуть методику Хэнсона (1975), на описании которой мы уже не можем останавливаться.
В методе Брауна (1950) используется принцип максимального правдоподобия, состоящий в том, что ищутся такие координаты вертекса, при которых зависящая от них так называемая функция правдоподобия L достигает максимума, т.е. удовлетворяются уравнения
|
|
(3.21) |
Здесь функция L имеет вид
|
|
(3.4) |
|
|
(3.23) |
(n - число звезд, φi - позиционные углы их собственных движений), a gi (vi)dvi - вероятность нахождения значения vi в интервале от vi до vi + dvi. Если средние квадратичные ошибки определения μα и μδ обозначить через σ(μα), σ(μδ), принять, что распределения μα и μδ относительно их истинных значений ξ и η являются гауссовыми, и ввести обозначения
|
|
(3.24) |
то можно показать, чтобы
![$$
g(v) = \frac{1}{\pi} \left[\left(\frac{c}{v^2 + c^2}\right) e^{-\frac{1}{2} b^2 (1+\frac{a^2}{c^2})} + \frac{b(av+c^2)}{(v^2 + c^2)^{3/2}} e^{-\frac{b^2 (v-a)^2}{2(v^2 + c^2)}} \int\limits_0^q e^{-\frac{t^2}{2}} dt \right] ,
$$](https://images.astronet.ru/pubd/2011/06/28/0001252610/tex/formula183.gif)
|
(3.25) |
|
|
(3.26) |
Зависимость функции L от A0, D0 определяется входящими в (3.25) и (3.26) величинами а, которые связаны с ними соотношением (3.24).
Нетрудно представить себе, насколько громоздко должны выглядеть написанные в явном виде уравнения (3.21). Поэтому в действительности они не используются. Вместо этого Браун предпочитает, задавая ряд меняющихся через 1 - 2°; возможных значений A0, D0, вычислять для каждой пары этих значений по приведенным выше формулам величину L. Найдя по ходу этих величин их максимум, можно найти и соответствующее наивероятнейшее значение координат A0, D0.
Оригинальный метод нахождения расстояния до движущегося скопления, не требующий знания координат вертекса, предложил Херцшпрунг (1919). Метод основан на определении годичного изменения угловых размеров скопления, обусловленного изменением расстояния между ним и Солнцем.
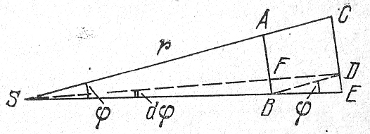
Рис. 14. Схема, поясняющая вывод формул (3.27)-(3.30).
Пусть на расстоянии r от Солнца S находится скопление, видимое под углом φ = &ang ASB (рис. 14). С увеличением расстояния на величину dr = АС угол φ уменьшается на величину dφ. Отрезки АВ и CD равны. Рассматривая треугольники SFB и DFB, находим:
|
|
(3.27) |
|
|
(3.28) |
Так как параллакс ![]() , и для определения π получаем формулу
, и для определения π получаем формулу
|
|
(3.29) |