Астронет > Движущиеся оболочки звезд

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Движущиеся оболочки звезд << 1.2 Степень возбуждения и ионизации | Оглавление | 1.4 О прозрачности среды для излучения в линиях >>

1.3 Относительные интенсивности линий

В предыдущем параграфе мы определили число атомов в каждом из состояний. Это дает возможность найти количество энергии, излучаемое средой в любой линии. Мы сейчас найдем относительные интенсивности бальмеровских линий (т. е. так называемый бальмеровский декремент) и некоторых линий ионизованного гелия.

Так как из общего числа квантов, излучаемых при переходе k → i, из среды выходит только для β_ik, то количество энергии, излучаемое единицей объема за единицу времени в частоте ν_ik и выходящее из среды, равно

$\begin{eqnarray} E_{ki} = n_k A_{ki} \beta_{ik} h\nu_{ik},\nonumber \end{eqnarray}$ (16)

или учитывая (8),

$\begin{eqnarray} E_{ki}=n_k\frac{\frac{g_2}{g_1}n_1-n_2}{\frac{g_k}{g_i}n_i-n_k}\left(\frac{\nu_{ik}}{\nu_{12}}\right)^3A_{21}\beta_{12}h\nu_{ik}.\nonumber \end{eqnarray}$ (17)

С помощью этой формулы для относительных интенсивностей бальмеровских линий (принимая интенсивность линии Н_β за единицу) получаем

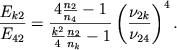
$\begin{eqnarray} \frac{E_{k2}}{E_{42}}=\frac{4 \frac{n_2}{n_4}-1}{\frac{k^2}{4}\frac{n_2}{n_k}-1}\left(\frac{\nu_{2k}}{\nu_{24}}\right)^4.\nonumber \end{eqnarray}$ (18)

Значения бальмеровского декремента, вычисленного по формуле (18) на основании данных таблиц II и III приведены в таблицах IV и V.

Таблица IV
Бальмеровский декремент
(T=20000°; )

x 0 0.01 0.1 1.0

H_α 0.67 0.98 2.00 5.20

H_β 1.00 1.00 1.00 1.00

H_γ 0.97 0.79 0.44 0.21

H_δ 0.87 0.58 0.22 0.06

Таблица V
Бальмеровский декремент
(T=50000°; )

x 0 0.1 1.0 10

H_α 0.62 0.72 1.05 1.80

H_β 1.00 1.00 1.00 1.00

H_γ 1.02 0.85 0.72 0.48

H_δ 0.93 0.65 0.48 0.29

Представляет также интерес отношение интенсивности бальмеровского континуума к интенсивности линий. Так как количество энергии, излучаемое за границей серии Бальмера, 1 см³ за 1 сек. равно [1]

$\begin{eqnarray} E_{c2}=5,52\cdot 10^{-23} n_e n^+ T^{-\frac{1}{2}},\nonumber \end{eqnarray}$ (19)

то для отношения $\frac{E_{c2}}{E_{k2}}$ находим

$\begin{eqnarray} \frac{E_{c2}}{E_{k2}}=\frac{7,3\cdot 10^{-21}}{xT^{\frac{1}{2}}} \frac{n_e n^+}{Wn_1} \frac{\frac{k^2}{4} \frac{n_2}{n_k}-1}{4-\frac{n_2}{n_1}}\left(\frac{\nu_{12}}{\nu_{2k}}\right)^4.\nonumber \end{eqnarray}$ (20)

С помощью таблиц I и II формула (20) дает, что при Т=20000°;, x=0,1 интенсивность бальмеровского континуума приблизительно в 4 раза больше интенсивности линии H_α. Как вытекает из сказанного ранее, табл. II, дающая ступень возбуждения водорода при Т=20000°;, дает одновременно и степень возбуждения ионизованного гелия при T=80000°;. Используя данные этой таблицы, мы вычислили относительные интенсивности трех следующих линий ионизованного гелия, представляющих наибольший интерес: λ 4686 (переход 4 → 3), λ 5411 (переход 7 → 4) и λ 6563 (переход 6 → 4). Результаты вычислений приведены в табл. VI.

Таблица VI
Относительные интенсивности линий He⁺
(T=80000^o)

x 0 0.01 0.1 1.0

E₄₃/E₇₄ 3.0 4.0 5.5 11

E₆₄/E₇₄ 0.7 0.9 1.0 1.5

В § 5 найденные нами относительные интенсивности линий будут сравнены с наблюдениями.

<< 1.2 Степень возбуждения и ионизации | Оглавление | 1.4 О прозрачности среды для излучения в линиях >>

Публикации с ключевыми словами: оболочки звезд - перенос излучения Публикации со словами: оболочки звезд - перенос излучения
См. также: Сбрасывающая массивную оболочку звезда G79.29+0.46 Обнаружение горячего водяного пара в оболочке углеродной звезды. Оболочки в туманности Яйцо Освещённость Планетарные туманности

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

x	0	0.01	0.1	1.0
H_α	0.67	0.98	2.00	5.20
H_β	1.00	1.00	1.00	1.00
H_γ	0.97	0.79	0.44	0.21
H_δ	0.87	0.58	0.22	0.06

x	0	0.1	1.0	10
H_α	0.62	0.72	1.05	1.80
H_β	1.00	1.00	1.00	1.00
H_γ	1.02	0.85	0.72	0.48
H_δ	0.93	0.65	0.48	0.29

x	0	0.01	0.1	1.0
E₄₃/E₇₄	3.0	4.0	5.5	11
E₆₄/E₇₄	0.7	0.9	1.0	1.5