1.1 Основные уравнения
Пусть ni - число атомов в i-м состоянии, n+- число ионизованных атомов и ne - число свободных электронов в 1 см3, соответственно. Число ионизаций с i-го уровня, происходящих в 1 см3 за 1 сек., мы обозначим через niBicρic, где Bic - эйнштейновский коэффициент поглощения и ρic - плотность излучения за границей i-й серии, число захватов на i-й уровень - через nen+Ci(Te), где Ci(Te) - некоторая функция от электронной температуры Te, и число спонтанных переходов с i-гo уровня на k-й - через niAik, где Aik - эйнштейновский коэффициент спонтанного перехода.
Если бы среда была неподвижной, то переходы с i-гo уровня на k-й в точности уравновешивались бы переходами с k-го уровня на i-й, так как все кванты, излучаемые в спектральных линиях, поглощались бы в самой среде. При наличии же градиента скорости число переходов с i-гo уровня на k-й будет больше числа обратных переходов, так как некоторая доля квантов в соответствующей линии уйдет из среды вследствие эффекта Допплера. Эту долю мы обозначим через βki. Тогда избыток числа переходов типа i → k над обратными переходами будет равен niAikβki.
В стационарном состоянии число переходов атомов из i-гo состояния во все другие должно равняться числу переходов в i-оe состояние. Вследствие этого мы получаем
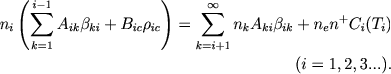
|
(1) |
В этих уравнениях величины ρic считаются известными и равными
|
|
(2) |
где ρic* - плотность излучения за границей i-й серии на поверхности звезды и W - коэффициент дилюции.
Прежде всего нам надо определить величины βik. Приступая к этому, мы допустим, что как коэффициент поглощения, так и коэффициент излучения в линии частоты νik отличны от нуля и постоянны в интервале Δνik, равном
|
|
(3) |
где u - средняя термическая скорость атомов и с - скорость света, и равны нулю вне этого интервала. Для коэффициента поглощения в линии мы имеем
|
|
(4) |
Когда излучение, выходящее из точки А, придет в точку В, находящуюся на расстоянии s от А, то оно будет ослаблено в eαiks раз и будет смещено по частоте на величину
|
|
(5) |
где ![]() - градиент скорости в среде. Следовательно, из излучения, выходящего из А, будет поглощена в среде лишь следующая часть:
- градиент скорости в среде. Следовательно, из излучения, выходящего из А, будет поглощена в среде лишь следующая часть:
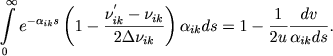
|
(6) |
Таким образом для величины βik мы находим
|
|
(7) |
Найденное выражение для βik мы должны подставить в уравнение (1). Но легко видеть, что
|
|
(8) |
Поэтому в результате подстановки мы получаем
![\begin{eqnarray} n_i\left[x\sum_{k=1}^{i-1} \frac{\frac{g_2}{g_1}n_1-n_2}{\frac{g_i}{g_k}n_k-n_i}\left(\frac{\nu_{ki}}{\nu_{12}}\right)^3+\frac{B_{ic}\rho_{ic}^*}{A_{21}}\right]=\nonumber\\
=x\sum_{k=i+1}^{\infty} n_k \frac{\frac{g_2}{g_1}n_1-n_2}{\frac{g_k}{g_i}n_i-n_k}\left(\frac{\nu_{ik}}{\nu_{12}}\right)^3+\frac{n_e n^+ C_i}{WA_{21}},\nonumber
\end{eqnarray}](https://images.astronet.ru/pubd/2011/06/28/0001252608/tex/formula21.gif)
|
(9) |
где обозначено
|
|
(10) |
Система уравнений (9) полностью определяет степень возбуждения и ионизации в среде, т. е. величины ![]() и
и ![]() . Параметрами, входящими в уравнения (9), кроме величины х, являются температура звезды (входящая через посредство Bicρic*) и температура среды (входящая через посредство Ci). Представляет интерес то обстоятельство, что параметром является лишь отношение градиента скорости к коэффициенту дилюции, а не каждая из этих величин в отдельности. Это значит, между прочим, что один и тот же градиент скорости сказывается на возбуждении и ионизации тем сильнее, чем меньше коэффициент дилюци.
. Параметрами, входящими в уравнения (9), кроме величины х, являются температура звезды (входящая через посредство Bicρic*) и температура среды (входящая через посредство Ci). Представляет интерес то обстоятельство, что параметром является лишь отношение градиента скорости к коэффициенту дилюции, а не каждая из этих величин в отдельности. Это значит, между прочим, что один и тот же градиент скорости сказывается на возбуждении и ионизации тем сильнее, чем меньше коэффициент дилюци.
Полученные нами уравнения относятся к случаю, когда среда непрозрачна для излучения во всех линиях. Допустим теперь, что среда прозрачна в линиях всех серий, начиная с j-й. Тогда, очевидно, в наших уравнениях мы должны положить
|
|
(11) |
Мы знаем, что газовые туманности полностью прозрачны для излучения в линиях субординатных серий и непрозрачны для излучения в линиях основной серии. Полагая в уравнениях (1) βik=1 (i = 2,3,4,...), β1k=0 и пренебрегая ионизацией из возбужденных состояний, получаем
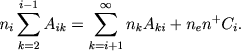
|
(12) |
<< Глава I. Однородная среда | Оглавление | 1.2 Степень возбуждения и ионизации >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |