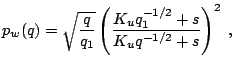<< 2.2. Эффект N 1: | Оглавление | 2.4. Эффект N 3: отражение >>
2.3. Эффект N 2: распространение в неоднородной среде
Теперь допустим, что облако неоднородно, но сжатия нет(
откуда находим
Соотношения (10) впервые выведены еще в 1944 г. соратником Альвена доктором Уаленом [9] опять же для развития теории солнечных пятен. Важно, что эти соотношения универсальны: они не зависят от геометрии магнитного поля.
Из свойства
![]() следует, что у АВ, бегущих
снаружи внутрь облака (в сторону увеличения плотности), амплитуда
возмущений скорости падает даже в отсутствие поглощения. Этим
эффектом можно объяснить [12] уменьшение ширины
спектральных линий к центру некоторых ПЗО.
следует, что у АВ, бегущих
снаружи внутрь облака (в сторону увеличения плотности), амплитуда
возмущений скорости падает даже в отсутствие поглощения. Этим
эффектом можно объяснить [12] уменьшение ширины
спектральных линий к центру некоторых ПЗО.
Отметим, что при выполнении приближения (6) второй
член справа в (5) можно преобразовать к виду
![]() , где учтено, что
, где учтено, что
![]() .
Тогда вместо (9) можно записать уравнение
.
Тогда вместо (9) можно записать уравнение
которое весьма часто используется в теории волн (например, [10]). Домашнее задание: с помощью уравнения (11) докажите, что при переходе звуковой волны из воздуха в стенку амплитуда возмущений скорости уменьшается в сотни раз.
Из соотношения
![]() следует, что давление
АВ,
следует, что давление
АВ,
![]() , помогает тепловому давлению бороться против
самогравитации облака, независимо от направления распространения
волны. Т. е. даже волны, входящие в облако снаружи, стараются его
расширить! Конечно, не надо забывать, что этот результат получен в
отсутствие поглощения волн и при условии, что распределение
амплитуды не зависит от времени. Если же поглощение входящей волны
велико, либо волна только начинает проникать в облако, то она
сдавливает облако и способствует коллапсу.
, помогает тепловому давлению бороться против
самогравитации облака, независимо от направления распространения
волны. Т. е. даже волны, входящие в облако снаружи, стараются его
расширить! Конечно, не надо забывать, что этот результат получен в
отсутствие поглощения волн и при условии, что распределение
амплитуды не зависит от времени. Если же поглощение входящей волны
велико, либо волна только начинает проникать в облако, то она
сдавливает облако и способствует коллапсу.
Сравнивая (8) и (10), мы видим, что в
покоящейся неоднородной среде зависимость ![]() гораздо
слабее, чем в однородно сжимающейся среде. Это различие
объясняется тем, что при сжатии часть энергии
крупномасштабного течения (порожденного, например,
самогравитацией) переходит в энергию волн. Интуиция подсказывает,
что если среда и неоднородна, и сжимается, то зависимость
гораздо
слабее, чем в однородно сжимающейся среде. Это различие
объясняется тем, что при сжатии часть энергии
крупномасштабного течения (порожденного, например,
самогравитацией) переходит в энергию волн. Интуиция подсказывает,
что если среда и неоднородна, и сжимается, то зависимость
![]() должна лежать между
должна лежать между
![]() и
и
![]() .
.
Оказывается, это предположение можно проверить аналитически, если предположить, что сжатие/расширение является стационарным. Используя ВКБ приближение, Паркер [13] нашел распределение амплитуды АВ в стационарном сферически симметричном звездном ветре. Несколько позже Белчер [14] показал, что результат Паркера может быть представлен как функция плотности, которую мы перепишем в виде
где
Заметим, что в случае очень медленного сжатия (
![]() )
соотношение (12) дает
)
соотношение (12) дает
![]() . В
противоположном случае получаем
. В
противоположном случае получаем
![]() .
Поведение
.
Поведение ![]() в случаях, когда скорость течения отрицательна и
по порядку величины близка к альвеновской скорости (
в случаях, когда скорость течения отрицательна и
по порядку величины близка к альвеновской скорости (
![]() ), показано на рис. 2.
), показано на рис. 2.
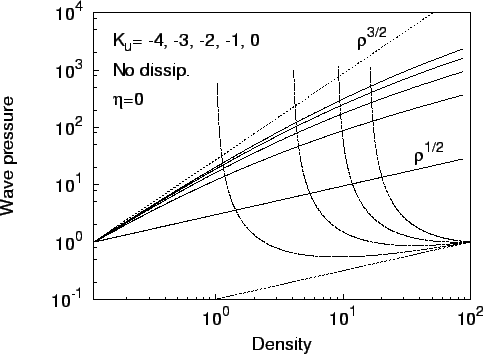 |
Рис. 2.
Зависимость волнового давления |
Видно, что функции ![]() существенно зависят от направления
распространения волны (знака
существенно зависят от направления
распространения волны (знака ![]() ). Если волна направлена против
течения, но альвеновская скорость меньше скорости течения, то
волна будет сноситься течением назад. В точке, где эти скорости
сравниваются, у волны, идущей против течения, должно происходить
бесконечное накопление энергии, однако при учете диссипативных
эффектов мы получим, что волна в этой точке полностью поглощается
(подъем штриховых кривых на рис. 2 сменится падением
к нулю).
). Если волна направлена против
течения, но альвеновская скорость меньше скорости течения, то
волна будет сноситься течением назад. В точке, где эти скорости
сравниваются, у волны, идущей против течения, должно происходить
бесконечное накопление энергии, однако при учете диссипативных
эффектов мы получим, что волна в этой точке полностью поглощается
(подъем штриховых кривых на рис. 2 сменится падением
к нулю).
Подводя итог, можно сказать, что конкуренция эффектов N 1 и N 2 определяется направлением распространения волны и отношением альвеновской скорости к скорости сжатия.
<< 2.2. Эффект N 1: | Оглавление | 2.4. Эффект N 3: отражение >>
|
Публикации с ключевыми словами:
МГД - альвеновские волны - Плазма
Публикации со словами: МГД - альвеновские волны - Плазма | |
См. также:
Все публикации на ту же тему >> | |