---

<< 1.5 Давление газа... | Оглавление | 1.7 Вариационный принцип >>

1.6 Основы термодинамики звезд

Ограничимся случаем химически однородной звезды. Одной из самых важных термодинамических функций вещества является удельная тепловая энергия . Пусть известна как функция удельного объема смг и удельной энтропии .

По I закону термодинамики . Поэтому, зная , можно найти и другие термодинамические величины. Например,

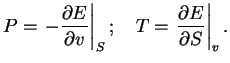
При заданной температуре иногда при расчетах удобно пользоваться свободной энергией системы :

Таким образом, . Однако при исследовании механической устойчивости равновесной звезды важно знать , так как процессы теплопроводности в звезде очень медленные и поэтому пульсации происходят адиабатически, т.е. с сохранением энтропии, но не температуры.

Введем еще одну важную термодинамическую функцию -- энтальпию

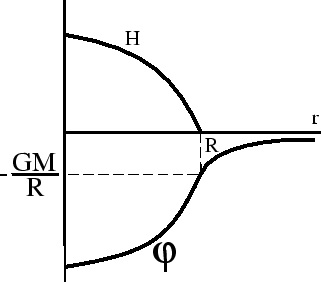
Если энтропия фиксирована, то . Используя это соотношение, запишем условие равновесия звезды в виде . Итак, для изэнтропических звезд ( const) условие равновесия есть const по звезде. На краю поэтому const. Внутри звезды энтальпия является ``зеркальным отражением'' (рис. 9).

Каков физический смысл соотношения const? Возьмем 1 г холодного вещества на бесконечности и поместим его в звезду на расстоянии от центра. Работа гравитационного поля при этом равна . Чтобы этот грамм находился в равновесии с веществом звезды, его необходимо нагреть до температуры окружающей среды , придать объем , т.е. совершить работу . Кроме этого, необходимо произвести работу , освобождая полость объема , в которую мы поместим наш элемент. Итак, полная работа равна . Условие const говорит о том, что затраченная работа не зависит от места, в котором мы размещаем элемент вещества.

Вместо того, чтобы брать элемент вещества на бесконечности, мы можем взять его в другом месте звезды. Тогда условие означает, что полная работа при перестановке двух элементов равна нулю, т.е. изэнтропическая звезда находится в безразличном равновесии относительно таких перестановок.

---

<< 1.5 Давление газа... | Оглавление | 1.7 Вариационный принцип >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также: Переработка вещества в Кассиопее А NGC 7789: Роза Каролины Планетарная туманность NGC 2818 от Хаббла Научная конференция "Наблюдаемые проявления эволюции звезд" в САО РАН Планетарные туманности Прошлые и будущие звёзды Андромеды Туманность Ожерелье Все публикации на ту же тему >>