<< 1.6 Основы термодинамики звезд | Оглавление | 1.8 Теорема вириала >>
1.7 Вариационный принцип
В химически однородной звезде необязательно переносить вещество: к тем же
результатам относительно устойчивости можно прийти, просто изменяя распределение
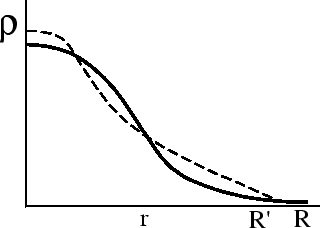
вещества ![]() , не меняя при этом взаимного расположения слоев
(рис. 10).
Можно утверждать, что если равновесие звезды слегка нарушить, то энергия при этом
не изменится. Точная формулировка этого утверждения: условие экстремума полной
энергии звезды
, не меняя при этом взаимного расположения слоев
(рис. 10).
Можно утверждать, что если равновесие звезды слегка нарушить, то энергия при этом
не изменится. Точная формулировка этого утверждения: условие экстремума полной
энергии звезды ![]() совпадает с условием равновесия.
совпадает с условием равновесия.
Рассматриваем звезду с произвольным распределением энтропии ![]() . Полная энергия
звезды
. Полная энергия
звезды ![]() складывается из тепловой энергии
складывается из тепловой энергии
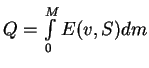 и гравитационной энергии1.2
и гравитационной энергии1.2
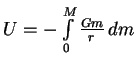 :
:
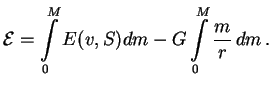
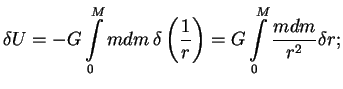
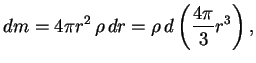 поэтому
поэтому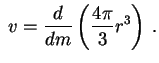
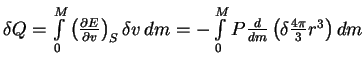 . Интегрируя по
частям с учетом того, что
. Интегрируя по
частям с учетом того, что
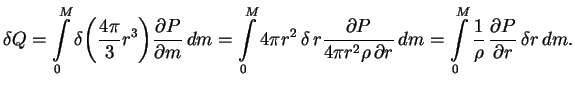
![$\displaystyle \delta {\cal{E}}=\int\limits_0^M dm \,\left[{1\over \rho} \,{\partial P \over \partial r}
+{Gm\over r^2}\right] \,\delta \,r.
$](https://images.astronet.ru/pubd/2008/02/15/0001226214/img267.gif)
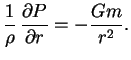
Чем полезен вариационный принцип? Оказывается, что с помощью этого принципа исследовать устойчивость много проще, чем используя уравнение равновесия. В этом можно убедиться следующим образом. Запишем выражение для полной энергии звезды, не предполагая равенства нулю скоростей движения вещества звезды:
![$\displaystyle {\cal{E}}=\int\limits_0^M \left[E(v,S)-{Gm\over r}+{u^2\over 2}\right] \,dm,
$](https://images.astronet.ru/pubd/2008/02/15/0001226214/img271.gif)
Помимо исследования устойчивости вариационный принцип позволяет находить приближенные решения для структуры звезды.
<< 1.6 Основы термодинамики звезд | Оглавление | 1.8 Теорема вириала >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |