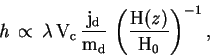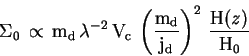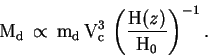<< 8. Некоторые результаты фотометри... | Оглавление | 8.2 Эллиптические галактики >>
8.1 Спиральные галактики
Уже свыше тридцати лет существует красивая легенда о том, что центральная
поверхностная яркость экспоненциальных дисков спиральных галактик -
![]() -- почти постоянна. В 1970 году Фриман [39] рассмотрел
выборку спиральных и S0 галактик с опубликованными ранее результатами
поверхностной фотометрии и нашел, что для 28 из 36 объектов выборки
-- почти постоянна. В 1970 году Фриман [39] рассмотрел
выборку спиральных и S0 галактик с опубликованными ранее результатами
поверхностной фотометрии и нашел, что для 28 из 36 объектов выборки
![]() . Поскольку поверхностная
яркость характеризует поверхностную плотность диска, вывод Фримана
накладывает жесткие ограничения на физические процессы формирования
и эволюции галактик, которые в результате должны привести к фиксированному
значению плотности для всех спиралей.
. Поскольку поверхностная
яркость характеризует поверхностную плотность диска, вывод Фримана
накладывает жесткие ограничения на физические процессы формирования
и эволюции галактик, которые в результате должны привести к фиксированному
значению плотности для всех спиралей.
С тех пор было выполнено множество работ, в которых этот результат
либо подтверждался (правда с большим по сравнению с оригинальным
результатом Фримана разбросом ![]() ) [182], либо
опровергался. Например, в [183,184] было показано, что
примерное постоянство значений
) [182], либо
опровергался. Например, в [183,184] было показано, что
примерное постоянство значений ![]() может быть объяснено эффектами
наблюдательной селекции (отбором подходящих для поверхностной фотометрии
галактик) и, следовательно, должны существовать (и их, возможно, очень
много) объекты с поверхностной яркостью гораздо меньшей фримановского
значения.
может быть объяснено эффектами
наблюдательной селекции (отбором подходящих для поверхностной фотометрии
галактик) и, следовательно, должны существовать (и их, возможно, очень
много) объекты с поверхностной яркостью гораздо меньшей фримановского
значения.
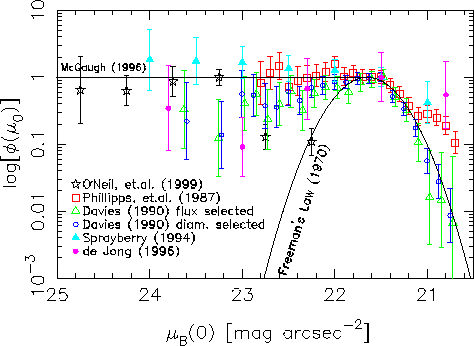
Современные данные об истинном, неискаженном селекцией, распределении
галактик по ![]() показаны на рис. 35. При
показаны на рис. 35. При
![]() это
распределение плоское, по-видимому, вплоть до
это
распределение плоское, по-видимому, вплоть до ![]() , хотя
можно допустить и то, что число галактик с ростом
, хотя
можно допустить и то, что число галактик с ростом ![]() постепенно
уменьшается.
''Закон Фримана'' описывает яркое крыло показанного на рис. 35 распределения
и очень сильно недооценивает число галактик с
постепенно
уменьшается.
''Закон Фримана'' описывает яркое крыло показанного на рис. 35 распределения
и очень сильно недооценивает число галактик с
![]() .
Наиболее наглядно противоречат ''закону Фримана'' так называемые
''галактики с низкой поверхностной яркостью'' (см. далее).
Например, существует ряд галактик, которые демонстрируют значения
центральной поверхностной яркости на
.
Наиболее наглядно противоречат ''закону Фримана'' так называемые
''галактики с низкой поверхностной яркостью'' (см. далее).
Например, существует ряд галактик, которые демонстрируют значения
центральной поверхностной яркости на ![]() (то есть на
(то есть на ![]() ) более слабые
по сравнению с
) более слабые
по сравнению с
![]() . Ярким
примером таких объектов является галактика Malin 1,
у которой
. Ярким
примером таких объектов является галактика Malin 1,
у которой
![]() [185]. Если допустить
справедливость ''закона Фримана'', то вероятность того, что
галактика имеет значение
[185]. Если допустить
справедливость ''закона Фримана'', то вероятность того, что
галактика имеет значение ![]() на
на ![]() отличающееся
от 21.65, равна
отличающееся
от 21.65, равна
![]() . Ориентировочное
число галактик во Вселенной составляет
. Ориентировочное
число галактик во Вселенной составляет
![]() и, следовательно,
галактики, подобные Malin 1, не должны наблюдаться.
и, следовательно,
галактики, подобные Malin 1, не должны наблюдаться.
 |
Существование большого числа слабых галактик не означает, что они дают
основной вклад в наблюдаемую плотность светимости галактик в окружающей
нас области Вселенной. Даже в случае, если распределение галактик по
![]() остается плоским до
остается плоским до ![]() , вклад объектов с низкой
поверхностной яркостью в плотность светимости не превышает 10%-30%.
Наибольший же вклад в создаваемую спиральными галактиками плотность
светимости дают объекты, подобные по своим интегральным характеристикам
нашей Галактике [187] (см. далее п. 8.3).
, вклад объектов с низкой
поверхностной яркостью в плотность светимости не превышает 10%-30%.
Наибольший же вклад в создаваемую спиральными галактиками плотность
светимости дают объекты, подобные по своим интегральным характеристикам
нашей Галактике [187] (см. далее п. 8.3).
На рис. 35 видно, что галактики с очень высокой центральной поверхностной
яркостью
очень редки. К таким объектам можно отнести взаимодействующие галактики,
у которых, как было показано в [60,188], среднее
значение ![]() примерно на 1
примерно на 1![]() ярче канонического значения Фримана.
Причиной повышенной яркости галактик в составе тесных взаимодействующих
систем является индуцированное гравитационным возмущением и переносом
массы активное звездообразование в их дисках и околоядерных областях.
ярче канонического значения Фримана.
Причиной повышенной яркости галактик в составе тесных взаимодействующих
систем является индуцированное гравитационным возмущением и переносом
массы активное звездообразование в их дисках и околоядерных областях.
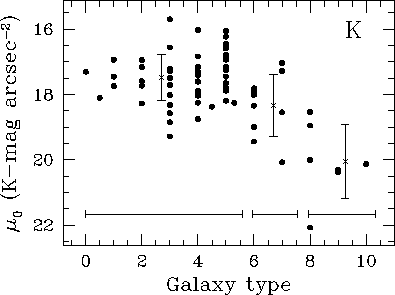 |
Значение ![]() слабо зависит от морфологического типа галактики,
хотя диски галактик поздних типов (
слабо зависит от морфологического типа галактики,
хотя диски галактик поздних типов (![]() ) являются, вероятно,
более слабыми [189,190] (см. рис. 36). Существует
зависимость
) являются, вероятно,
более слабыми [189,190] (см. рис. 36). Существует
зависимость ![]() от полной светимости (массы) спиральной галактики --
с ростом светимости поверхностная яркость увеличивается [191].
от полной светимости (массы) спиральной галактики --
с ростом светимости поверхностная яркость увеличивается [191].
В [192] предложена следующая простая классификация
спиральных галактик в зависимости от значения ![]() :
:
- --- галактики с очень высокой поверхностной яркостью:
- --- с высокой поверхностной яркостью (''фримановские''):
- --- с промежуточной яркостью:
- --- с низкой поверхностной яркостью (LSB):
![]() Экспоненциальный масштаб
Экспоненциальный масштаб
Масштаб звездных дисков спиральных галактик ![]() слабо зависит от
морфологического типа [189]. Для ярких, сравнимых с Млечным
Путем, галактик он варьируется в основном от 1 до 10 кпк.
слабо зависит от
морфологического типа [189]. Для ярких, сравнимых с Млечным
Путем, галактик он варьируется в основном от 1 до 10 кпк.
Значение ![]() зависит от цветовой полосы -- с увеличением длины волны
экспоненциальный масштаб, в среднем, уменьшается. Согласно данным
для 86 видимых почти ''плашмя'' спиралей из [138] среднее
значение отношения
зависит от цветовой полосы -- с увеличением длины волны
экспоненциальный масштаб, в среднем, уменьшается. Согласно данным
для 86 видимых почти ''плашмя'' спиралей из [138] среднее
значение отношения
![]() .
Этот вывод подтверждается и данными для спиральных галактик, видимых
под большими углами к лучу зрения, --
.
Этот вывод подтверждается и данными для спиральных галактик, видимых
под большими углами к лучу зрения, --
![]() ,
,
![]() [190].
Кроме того, отношение значений
[190].
Кроме того, отношение значений ![]() в разных цветовых полосах зависит
от типа галактики, что, вероятно, отражает изменение
содержания пыли вдоль морфологической последовательности [190].
в разных цветовых полосах зависит
от типа галактики, что, вероятно, отражает изменение
содержания пыли вдоль морфологической последовательности [190].
На периферии дисков галактик (при
![]() [110,193])
экспоненциальное уменьшение яркости сменяется резким падением,
''обрывом''. Причина этого являения неясна. Возможно, к примеру, что
радиус ''обрезания'' звездного диска -- это расстояние, на котором
плотность газа становится ниже требуемого для процесса
звездообразования критического значения [194].
[110,193])
экспоненциальное уменьшение яркости сменяется резким падением,
''обрывом''. Причина этого являения неясна. Возможно, к примеру, что
радиус ''обрезания'' звездного диска -- это расстояние, на котором
плотность газа становится ниже требуемого для процесса
звездообразования критического значения [194].
![]() Диаграмма
Диаграмма ![]() -
-![]()
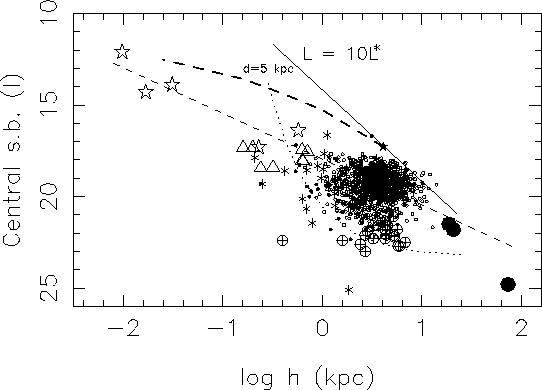
На рис. 37 приведено распределение характеристик экспоненциальных дисков
галактик разных типов в полосе ![]() на плоскости
на плоскости ![]() -
-![]() [195]
(H
[195]
(H![]() =75 км/с/Мпк).
Маленькими кружками изображены данные для >1000 Sb-Sd спиралей
из [196] (черными кружками показаны
параметры галактик с расстоянием
=75 км/с/Мпк).
Маленькими кружками изображены данные для >1000 Sb-Sd спиралей
из [196] (черными кружками показаны
параметры галактик с расстоянием ![]() 15 Мпк), звезды -- компактные ядерные
диски в ядрах E/S0 галактик, треугольники и звездочки -- звездные диски
в E/S0 галактиках, кружки с крестами -- галактики с низкой поверхностной
яркостью, большие черные кружки -- гигантские галактики с низкой
поверхностной яркостью. Толстой непрерывной прямой изображена линия
постоянной светимости диска с полной светимостью, равной 10
15 Мпк), звезды -- компактные ядерные
диски в ядрах E/S0 галактик, треугольники и звездочки -- звездные диски
в E/S0 галактиках, кружки с крестами -- галактики с низкой поверхностной
яркостью, большие черные кружки -- гигантские галактики с низкой
поверхностной яркостью. Толстой непрерывной прямой изображена линия
постоянной светимости диска с полной светимостью, равной 10![]() ;
пунктирная кривая -- линия селекции для галактик с диаметром 5 кпк
(выборка [196] ограничена по угловому диаметру -- в нее включены
галактики с диаметром
;
пунктирная кривая -- линия селекции для галактик с диаметром 5 кпк
(выборка [196] ограничена по угловому диаметру -- в нее включены
галактики с диаметром ![]() );
штриховая кривая соответствует условию устойчивости по отношению к
формированию бара для диска с
);
штриховая кривая соответствует условию устойчивости по отношению к
формированию бара для диска с
![]() = 10
= 10![]() ; штриховая прямая -- зависимость
; штриховая прямая -- зависимость
![]() .
.
На рисунке видно, что характеристики дисков реальных галактик
располагаются на этой плоскости
в очень широком диапазоне поверхностных яркостей
(
![]() ) и размеров (
) и размеров (![]() 10 пк -- 100 кпк),
образуя непрерывную последовательность. Вдоль этой последовательности
систематически изменяется отношение светимостей балджа
и диска -- от >10 для эллиптических галактик в левом верхнем
углу рис. 37 до
10 пк -- 100 кпк),
образуя непрерывную последовательность. Вдоль этой последовательности
систематически изменяется отношение светимостей балджа
и диска -- от >10 для эллиптических галактик в левом верхнем
углу рис. 37 до ![]() у спиральных галактик в нижнем правом углу.
Отношение эффективного радиуса балджа
у спиральных галактик в нижнем правом углу.
Отношение эффективного радиуса балджа ![]() и масштаба диска
и масштаба диска
![]() варьируется от
варьируется от ![]() для гигантских галактик с низкой
поверхностной яркостью в правом нижнем углу рисунка до значений
для гигантских галактик с низкой
поверхностной яркостью в правом нижнем углу рисунка до значений
![]() 5-10 для звездных дисков в E/S0 галактиках.
Вдоль этой же последовательности изменяются и
значения
5-10 для звездных дисков в E/S0 галактиках.
Вдоль этой же последовательности изменяются и
значения ![]() и
и ![]() -- диски галактик с большими значениями
отношения
-- диски галактик с большими значениями
отношения ![]() являются, в среднем, более компактными и яркими
(см. также рис. 36).
являются, в среднем, более компактными и яркими
(см. также рис. 36).
Положение характеристик галактик на
плоскости ![]() -
-![]() определяется требованием устойчивости дисков,
ограничением их полной светимости (
определяется требованием устойчивости дисков,
ограничением их полной светимости (
![]() ) и
наблюдательной селекцией при их отборе. Сочетание этих трех
условий (а также, возможно, еще неизвестных факторов) приводит
к выстраиванию характеристик дисков галактик вдоль эмпирической
зависимости
) и
наблюдательной селекцией при их отборе. Сочетание этих трех
условий (а также, возможно, еще неизвестных факторов) приводит
к выстраиванию характеристик дисков галактик вдоль эмпирической
зависимости
![]() (рис. 37). Более глубокие
(в смысле поверхностной яркости) обзоры должны
привести, вероятно, к ``размыванию'' этой наблюдательной зависимости,
однако, она должна сохраниться в виде верхней границы распределения
параметров галактик.
(рис. 37). Более глубокие
(в смысле поверхностной яркости) обзоры должны
привести, вероятно, к ``размыванию'' этой наблюдательной зависимости,
однако, она должна сохраниться в виде верхней границы распределения
параметров галактик.
Количественная интерпретация диаграммы ![]() -
-![]() может быть получена
на основе простых масштабных соотношений, получаемых в модели формирования
диска, описанной Мо и др. [197]9.
Подход Мо и др. [197] основан на CDM (Cold Dark Matter,
холодная скрытая масса) сценарии формирования галактик.
Согласно этому сценарию, на первом этапе из первичных флуктуаций
плотности формируются гало, состоящие из материи в небарионной форме.
Затем в этих гало охлаждается и конденсируется газ, образуя
диски наблюдаемых вокруг нас галактик.
может быть получена
на основе простых масштабных соотношений, получаемых в модели формирования
диска, описанной Мо и др. [197]9.
Подход Мо и др. [197] основан на CDM (Cold Dark Matter,
холодная скрытая масса) сценарии формирования галактик.
Согласно этому сценарию, на первом этапе из первичных флуктуаций
плотности формируются гало, состоящие из материи в небарионной форме.
Затем в этих гало охлаждается и конденсируется газ, образуя
диски наблюдаемых вокруг нас галактик.
Основные предположения, сделанные в [197], состоят в следующем:
- масса диска галактики (M
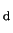 ) является фиксированной долей (m
) является фиксированной долей (m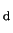 )
массы темного гало (M), в которое диск погружен -
M
)
массы темного гало (M), в которое диск погружен -
M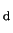 =m
=m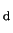 M;
M;
- угловой момент диска (J
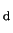 ) также
составляет фиксированную долю (j
) также
составляет фиксированную долю (j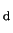 )
углового момента гало (J) -- J
)
углового момента гало (J) -- J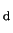 =j
=j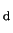 J;
J;
- диски галактик являются
тонкими, их равновесие поддерживается вращением
и они имеют экспоненциальное распределение плотности
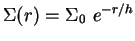 , где
, где 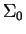 -- центральная
поверхностная плотность диска, а
-- центральная
поверхностная плотность диска, а 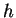 -- его экспоненциальный масштаб;
-- его экспоненциальный масштаб;
- диски реальных галактик являются устойчивыми.
На основе этих предположений можно получить (см. [197]), что
и
В формулах (86-88) ![]() -- это безразмерный
угловой момент,
определяемый стандартным образом как
-- это безразмерный
угловой момент,
определяемый стандартным образом как
![]() =J
=J![]() E
E![]()
![]() M
M![]() (E -- полная энергия гало,
(E -- полная энергия гало,
![]() -- гравитационная постоянная), V
-- гравитационная постоянная), V![]() -- скорость вращения диска,
H
-- скорость вращения диска,
H![]() -- значение постоянной Хаббла в настоящую эпоху, а
H(
-- значение постоянной Хаббла в настоящую эпоху, а
H(![]() ) -- постоянная Хаббла при красном смещении
) -- постоянная Хаббла при красном смещении ![]() , при котором
сформировалось темное гало, внутри которого образовался
диск. H(
, при котором
сформировалось темное гало, внутри которого образовался
диск. H(![]() ), естественно, зависит от принятой космологической
модели.
), естественно, зависит от принятой космологической
модели.
Согласно описываемому сценарию, основные свойства дисковых галактик
полностью определяются значениями ![]() , m
, m![]() , j
, j![]() , V
, V![]() и H(
и H(![]() ). Поскольку величина H(
). Поскольку величина H(![]() ) растет с
) растет с ![]() , то, как видно
из соотношений (86) и (87), сформировавшиеся при
больших
, то, как видно
из соотношений (86) и (87), сформировавшиеся при
больших ![]() диски
должны быть более компактными и иметь большую плотность (при
неизменных значениях остальных параметров). Большим значениям
диски
должны быть более компактными и иметь большую плотность (при
неизменных значениях остальных параметров). Большим значениям
![]() должны соответствовать протяженные и относительно
менее плотные диски.
должны соответствовать протяженные и относительно
менее плотные диски.
Отметим, что аналитические выражения для глобальных характеристик
дисков галактик
приводятся также в работах других авторов. Например, в
[200] получено, что
![]() и
и
![]() , где
, где ![]() -- это
относительная доля массы галактики в барионной форме. При малых
значениях
-- это
относительная доля массы галактики в барионной форме. При малых
значениях ![]() модель [200] предсказывает
зависимость параметров диска от
модель [200] предсказывает
зависимость параметров диска от ![]() и M близкую к найденной в [197].
Аналогичные зависимости были получены ранее и ван дер Круитом [182].
Однако в работе Мо и др. эти соотношения представлены
в наиболее удобной для исследования форме. Кроме того, в них
в явной форме входит зависимость параметров диска от времени его
формирования.
и M близкую к найденной в [197].
Аналогичные зависимости были получены ранее и ван дер Круитом [182].
Однако в работе Мо и др. эти соотношения представлены
в наиболее удобной для исследования форме. Кроме того, в них
в явной форме входит зависимость параметров диска от времени его
формирования.
Полная светимость диска на основе (86) и (87) может
быть представлена как
![]() V
V![]() .
(Таким образом, модель [197] содержит ``встроенное'' соотношение
Талли-Фишера.) Спиральные галактики из диссертации [196]
демонстрируют зависимость
.
(Таким образом, модель [197] содержит ``встроенное'' соотношение
Талли-Фишера.) Спиральные галактики из диссертации [196]
демонстрируют зависимость
![]() с коэффициентом корреляции
с коэффициентом корреляции ![]() .
Согласно (86-87), для дисков галактик должны
приближенно выполняться соотношения
.
Согласно (86-87), для дисков галактик должны
приближенно выполняться соотношения
![]() lg V
lg V![]() и lg
и lg ![]() lg V
lg V![]() (при фиксированных значениях
(при фиксированных значениях
![]() , m
, m![]() , j
, j![]() и
и ![]() ). Спиральные галактики из [196]
следуют близким зависимостям:
). Спиральные галактики из [196]
следуют близким зависимостям:
![]() lg
lg ![]() (
(![]() )
и lg
)
и lg ![]() 0.70lg
0.70lg ![]() (
(![]() ).
).
Подробные исследования показали, что
простые масштабные соотношения, получаемые в модели формирования
дисков в рамках CDM сценария, в первом приближении удовлетворительно
описывают параметры
спиральных галактик и их рассеяние на диаграмме ![]() -
-![]() [197,195]. (В наибольшей степени от предсказаний сценария
[197] уклоняются характеристики компактных дисков в галактиках
ранних типов. По-видимому, механизм образования дисков в таких объектах
отличается от описанного выше.) Следует, однако, отметить, что
в подходе Мо и др. не учтены такие
важные процессы, модифицирующие характеристики галактик, как
звездообразование и механизм обратной связи, внешняя аккреция
и слияния.
[197,195]. (В наибольшей степени от предсказаний сценария
[197] уклоняются характеристики компактных дисков в галактиках
ранних типов. По-видимому, механизм образования дисков в таких объектах
отличается от описанного выше.) Следует, однако, отметить, что
в подходе Мо и др. не учтены такие
важные процессы, модифицирующие характеристики галактик, как
звездообразование и механизм обратной связи, внешняя аккреция
и слияния.
![]() Толщина звездных дисков
Толщина звездных дисков
Наблюдаемая толщина звездных дисков видимых ''с ребра'' галактик
зависит от вертикальной дисперсии скоростей звезд и плотности
диска (см. п. 5.2). Наблюдения показывают, что вертикальный масштаб
распределения поверхностной яркости (![]() ,
, ![]() -- уравнения
(54-55)) почти не меняется (вариации масштаба
не превышают 10-15%) в пределах оптического
диска галактики [110,201,202]. (Это утверждение,
по-видимому, справедливо для большинства спиральных галактик
поздних типов. У галактик ранних типов --
-- уравнения
(54-55)) почти не меняется (вариации масштаба
не превышают 10-15%) в пределах оптического
диска галактики [110,201,202]. (Это утверждение,
по-видимому, справедливо для большинства спиральных галактик
поздних типов. У галактик ранних типов -- ![]() --
часто встречаются расширяющиеся к периферии звездные диски [203].)
Следовательно (п. 5.2),
вертикальная дисперсия
--
часто встречаются расширяющиеся к периферии звездные диски [203].)
Следовательно (п. 5.2),
вертикальная дисперсия ![]() связана с поверхностной
яркостью диска следующим образом:
связана с поверхностной
яркостью диска следующим образом:
![]() .
Таким образом, результаты поверхностной фотометрии наблюдаемых
''с ребра'' галактик приводят к выводу, что в экспоненциальных
дисках спиралей значение
.
Таким образом, результаты поверхностной фотометрии наблюдаемых
''с ребра'' галактик приводят к выводу, что в экспоненциальных
дисках спиралей значение ![]() должно изменяться
должно изменяться
![]() , где
, где ![]() -- радиальный масштаб диска.
Этот вывод подтверждается непосредственными измерениями дисперсии скоростей
звезд в спиральных галактиках (например, [204]).
-- радиальный масштаб диска.
Этот вывод подтверждается непосредственными измерениями дисперсии скоростей
звезд в спиральных галактиках (например, [204]).
Характерное значение вертикального масштаба для дисков нормальных
спиральных галактик составляет
![]() кпк (напомним, что
вдали от плоскости галактики
кпк (напомним, что
вдали от плоскости галактики ![]() ). Определяемые из наблюдений
величины
). Определяемые из наблюдений
величины ![]() мало зависят от цветовой полосы [201,202].
мало зависят от цветовой полосы [201,202].
Как следует из теоретических соображений, вертикальная структура
дисков чувствительна к внешнему возмущению и аккреции
вещества [205]. При гравитационном взаимодействии часть
энергии орбитального движения галактик может перейти в их внутреннюю
энергию и ''разогреть'' их диски, то есть увеличить ![]() и,
следовательно, наблюдаемую толщину. В аналитическом исследовании
[205] было показано, что прирост толщины диска на данном
расстоянии
и,
следовательно, наблюдаемую толщину. В аналитическом исследовании
[205] было показано, что прирост толщины диска на данном
расстоянии ![]() от центра
от центра
![]() ,
где
,
где ![]() -- исходная толщина диска, M
-- исходная толщина диска, M![]() -- полная масса
упавших на галактику спутников, M
-- полная масса
упавших на галактику спутников, M![]() -- масса диска галактики.
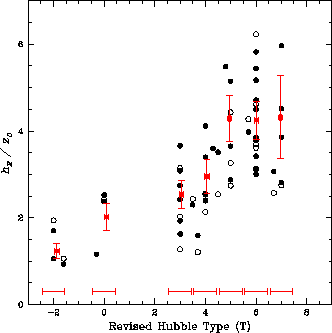
Следовательно, можно ожидать, что объекты в составе тесных
взаимодействующих систем, а также галактики, испытавшие значительную
внешнюю аккрецию (например, ''проглотившие'' массивный спутник)
будут иметь наиболее толстые звездные диски. Эффект приливного утолщения
был, действительно, открыт при сравнении распределений яркости в
вертикальном направлении в выборках взаимодействующих и относительно
изолированных галактик [202]. Оказалось, что галактики во
взаимодействующих системах демонстрируют в 1.5-2 раза более толстые
диски (на расстоянии
-- масса диска галактики.
Следовательно, можно ожидать, что объекты в составе тесных
взаимодействующих систем, а также галактики, испытавшие значительную
внешнюю аккрецию (например, ''проглотившие'' массивный спутник)
будут иметь наиболее толстые звездные диски. Эффект приливного утолщения
был, действительно, открыт при сравнении распределений яркости в
вертикальном направлении в выборках взаимодействующих и относительно
изолированных галактик [202]. Оказалось, что галактики во
взаимодействующих системах демонстрируют в 1.5-2 раза более толстые
диски (на расстоянии ![]() 1
1![]() -2
-2![]() от ядра)
по сравнению с галактиками тех же типов и светимостей в более
бедном пространственном окружении (рис. 38).
от ядра)
по сравнению с галактиками тех же типов и светимостей в более
бедном пространственном окружении (рис. 38).
 |
 |
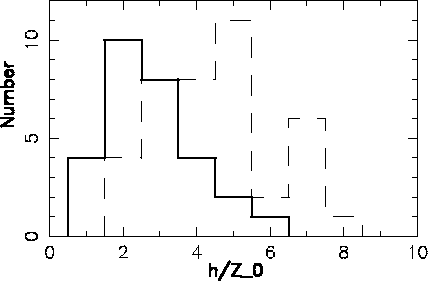
Относительная толщина звездных дисков -- отношение вертикального и
радиального масштабов распределений поверхностной яркости -- зависит
от физических характеристик и типа галактики. Согласно [202],
отношение ![]() для нормальных, невзаимодействующих галактик
коррелирует с относительным содержанием нейтрального
водорода --
для нормальных, невзаимодействующих галактик
коррелирует с относительным содержанием нейтрального
водорода --
![]() ,
где
,
где ![]() -- полная светимость галактики в положении ''с ребра''
в полосе
-- полная светимость галактики в положении ''с ребра''
в полосе ![]() . Следовательно, богатые газом спирали должны быть
более тонкими. Содержание HI, как и многие другие характеристики,
плавно изменяется вдоль Хаббловской последовательности и поэтому
можно ожидать, что отношение
. Следовательно, богатые газом спирали должны быть
более тонкими. Содержание HI, как и многие другие характеристики,
плавно изменяется вдоль Хаббловской последовательности и поэтому
можно ожидать, что отношение ![]() зависит от типа галактики и других,
коррелирующих с типом, параметров. В работах [206,190,207]
было показано, что толщина звездных дисков связана с
показателем цвета, абсолютной светимостью и морфологическим типом
галактик (см. пример на рис. 39) -- более голубые, слабые и имеющие
более поздние морфологические типы спирали являются, в среднем, более
тонкими.
зависит от типа галактики и других,
коррелирующих с типом, параметров. В работах [206,190,207]
было показано, что толщина звездных дисков связана с
показателем цвета, абсолютной светимостью и морфологическим типом
галактик (см. пример на рис. 39) -- более голубые, слабые и имеющие
более поздние морфологические типы спирали являются, в среднем, более
тонкими.
Связь толщины диска с содержанием газа и ![]() может быть
объяснена активным звездообразованием в плоскости
богатых газом галактик поздних типов, которое повышает поверхностную
яркость в тонком слое вблизи плоскости и эффективно уменьшает определяемое
из наблюдений значение вертикального масштаба. С другой стороны,
как было предположено в [208],
эта корреляция может отражать найденное в [209] из соображений
устойчивости соотношение между толщиной диска и массой темного гало,
относительный вклад которого увеличивается при переходе к более
поздним морфологическим типам.
может быть
объяснена активным звездообразованием в плоскости
богатых газом галактик поздних типов, которое повышает поверхностную
яркость в тонком слое вблизи плоскости и эффективно уменьшает определяемое
из наблюдений значение вертикального масштаба. С другой стороны,
как было предположено в [208],
эта корреляция может отражать найденное в [209] из соображений
устойчивости соотношение между толщиной диска и массой темного гало,
относительный вклад которого увеличивается при переходе к более
поздним морфологическим типам.
![]() Распределение показателей цвета
Распределение показателей цвета
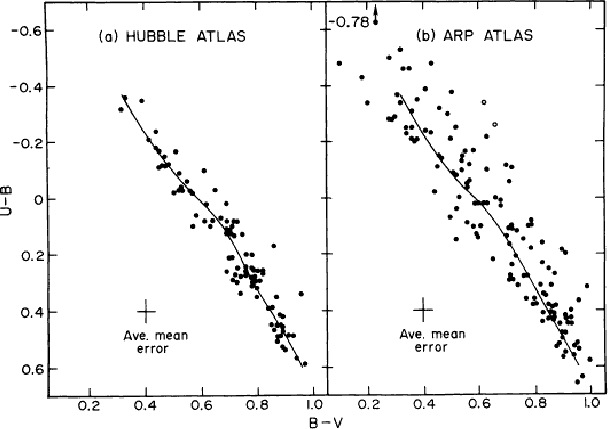 |
Показатели цвета галактик характеризуют распределение энергии в их спектрах и зависят от истории звездообразования в них. На двухцветных диаграммах галактики выстраиваются в относительно узкую полосу (см. пример на рис. 40). Интерпретация этих диаграмм производится с помощью метода эволюционного моделирования, позволяющего оценить (хотя бы в первом приближении) звездный состав и историю звездообразования в галактике [211]. В частности, анализ показанных на рис. 40 диаграмм привел Ларсона и Тинсли [210] к выводу, что взаимодействие между галактиками может стимулировать в них вспышки звездообразования.
У спиральных галактик, подобно эллиптическим, наблюдается связь абсолютной звездной величины с показателями цвета -- более яркие (массивные) галактики являются более красными [212].
Использование интегральных показателей цвета, например, найденных
с помощью многоапертурной фотометрии, при исследовании конкретных
галактик может привести к существенной потере информации. Распределение
яркости в галактиках сконцентрировано к центру и поэтому основной
вклад в интегральные цвета дает лишь относительно небольшая часть их площади.
Например, эффективный радиус экспоненциального диска равен
1.68![]() (п. 5.1), в то время как звездные диски галактик прослеживаются до
(п. 5.1), в то время как звездные диски галактик прослеживаются до
![]() 5
5![]() . Следовательно, половина полной светимости чисто
дисковой галактики излучается с
. Следовательно, половина полной светимости чисто
дисковой галактики излучается с ![]() 1/5-1/10 ее
полной площади.
Поэтому для создания реалистических моделей галактик, для детального
исследования звездообразования в них необходимо исследовать
распределение показателей цвета по дискам.
1/5-1/10 ее
полной площади.
Поэтому для создания реалистических моделей галактик, для детального
исследования звездообразования в них необходимо исследовать
распределение показателей цвета по дискам.
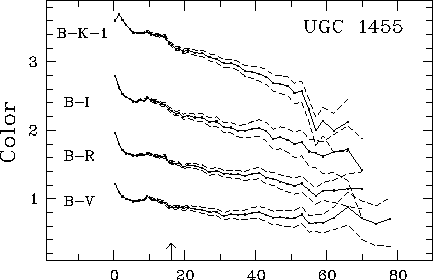
Наблюдения показывают, что для видимых ''плашмя'' спиральных галактик характерно систематическое уменьшение показателей цвета (''поголубение'') с удалением от центра (например, [213]) -- см. рис. 41. В пределах данной галактики существует четкая корреляция между поверхностной яркостью и показателем цвета -- чем меньше поверхностная яркость, тем голубее эта область. Радиальные градиенты цветов в спиралях скорее всего объясняются комбинированным эффектом поглощения пылью (п. 7.1) и градиентом возраста звезд и их металличности вдоль дисков [213].
 |
У видимых ''с ребра'' спиральных галактик вдали от их плоскостей
(при
![]() ) вертикальные градиенты показателей
цвета малы или практически отсутствуют (особенно у дисков галактик
ранних морфологических типов) [214].
) вертикальные градиенты показателей
цвета малы или практически отсутствуют (особенно у дисков галактик
ранних морфологических типов) [214].
![]() Балджи спиральных галактик и отношение B/D
Балджи спиральных галактик и отношение B/D
Для описания распределения поверхностной яркости
в балджах спиральных галактик обычно используют закон Вокулера
(формула (11)). Часто рассматривают также более общую
формулу Серсика (25) [215]. Оказалось, что
параметр ![]() в формуле Серсика, определяющий закон распределения
яркости, зависит от морфологического типа спиральной галактики,
от отношения светимостей балджа и диска
в формуле Серсика, определяющий закон распределения
яркости, зависит от морфологического типа спиральной галактики,
от отношения светимостей балджа и диска ![]() и от характеристик
самого балджа (его светимости, эффективного радиуса и центральной
поверхностной яркости) [215,216,217]. Так, для
галактик поздних
морфологических типов (
и от характеристик
самого балджа (его светимости, эффективного радиуса и центральной
поверхностной яркости) [215,216,217]. Так, для
галактик поздних
морфологических типов (![]() )
) ![]() , то есть балджи таких
галактик могут быть описаны экспоненциальным законом (43).
Балджи галактик ранних типов (
, то есть балджи таких
галактик могут быть описаны экспоненциальным законом (43).
Балджи галактик ранних типов (![]() ) характеризуются значением
) характеризуются значением
![]() , то есть они могут быть представлены формулой Вокулера
(11).
, то есть они могут быть представлены формулой Вокулера
(11).
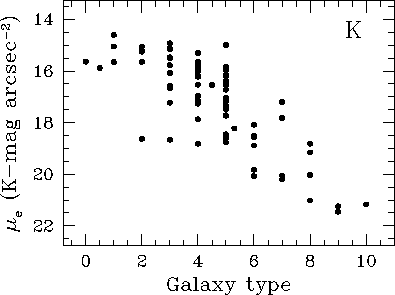
При смещении вдоль Хаббловской последовательности от спиральных галактик ранних типов к поздним уменьшается средняя светимость балджа и его эффективная поверхностная яркость (рис. 42). Эффективный радиус балджа от типа галактики практически не зависит [189].
 |
В таблице 6 приведены средние значения отношения ![]() в цветовой полосе
в цветовой полосе
![]() для нормальных галактик разных морфологических типов типов
согласно [131] (для описания диска использован экспоненциальный
закон, а для балджа -- закон Вокулера).
для нормальных галактик разных морфологических типов типов
согласно [131] (для описания диска использован экспоненциальный
закон, а для балджа -- закон Вокулера).
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0.9 | 0.7 | 0.5 | 0.3 | 0.2 | 0.1 | 0.05 | 0.02 |
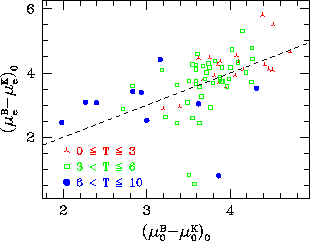
Показатели цвета балджей, в среднем, краснее показателей цвета дисков, однако они близки к цветам их -- дисков -- центральных областей [218,213] (рис. 43). Диапазон изменения показателей цвета балджей довольно велик и существуют ''голубые'' балджи.
 |
Размеры балджей статистически связаны с размерами дисков, в которые
они погружены: если приблизить распределение яркости в балдже
экспоненциальным законом, то его экспоненциальный масштаб будет составлять
![]() 1/10 масштаба диска, причем эта корреляция выражена лучше
для спиральных галактик поздних типов [219].
1/10 масштаба диска, причем эта корреляция выражена лучше
для спиральных галактик поздних типов [219].
Фотометрические характеристики балджей (![]() или
или
![]() и
и ![]() ) располагаются на плоскости эффективных параметров
(см. далее п. 8.2) примерно также как и характеристики эллиптических галактик.
В работе [220] обнаружено, что
балджи и эллиптические галактики в пространстве своих глобальных
фотометрических параметров (
) располагаются на плоскости эффективных параметров
(см. далее п. 8.2) примерно также как и характеристики эллиптических галактик.
В работе [220] обнаружено, что
балджи и эллиптические галактики в пространстве своих глобальных
фотометрических параметров (![]() -- показатель степени в формуле Серсика,
-- показатель степени в формуле Серсика,
![]() ,
, ![]() -- центральная поверхностная балджа или E галактики)
образуют единую плоскость: lg
-- центральная поверхностная балджа или E галактики)
образуют единую плоскость: lg![]() =
= ![]() lg
lg![]() +
+ ![]()
![]() + const.
В полосе
+ const.
В полосе ![]() численные значения коэффициентов равны:
численные значения коэффициентов равны: ![]() =0.17,
=0.17, ![]() =-0.07 и
const=1.18 [220]. Очевидно, что соотношение Корменди
является частным случаем этой трехпараметрической зависимости при
=-0.07 и
const=1.18 [220]. Очевидно, что соотношение Корменди
является частным случаем этой трехпараметрической зависимости при
![]() =4 (напомним, что
=4 (напомним, что
![]() (п. 4.1.1)).
(п. 4.1.1)).
Относительные вклады балджей и дисков в среднюю плотность вещества Вселенной примерно одинаковы [221].
Корреляция цветов балджей и дисков, связь их характерных масштабов -
все это стимулировало активное обсуждение вопроса о возможности
формирования балджей в процессе медленной динамической эволюции
дисков (например, за счет бароподобной неустойчивости) [222].
Балджи очень неоднородны по своим характеристикам и, возможно, они
могут формироваться в ходе разных процессов: при первичном коллапсе,
при внешней аккреции и слияниях галактик, за счет эволюции диска и т.д.
![]() Масштабные соотношения для дисков галактик
Масштабные соотношения для дисков галактик
 |
Неоднократно предпринимались попытки построить по аналогии с
эллиптическими галактиками (см. далее п. 8.2) трехпараметрическую зависимость,
объединяющую фотометрические и кинематические характеристики дисков спиральных
галактик (например, [223,224,225] и ссылки там же).
В [225] было показано, что в трехпараметрическом пространстве
![]() (светимость),
(светимость), ![]() (радиус), V (скорость вращения) спиральные галактики
распределяются в пределах плоскости
(радиус), V (скорость вращения) спиральные галактики
распределяются в пределах плоскости
![]() (авторы предложили называть ее масштабной плоскостью).
Известные эмпирические соотношения (Талли-Фишера, ''закон Фримана'')
могут являться проекциями этой плоскости на различные оси.
(авторы предложили называть ее масштабной плоскостью).
Известные эмпирические соотношения (Талли-Фишера, ''закон Фримана'')
могут являться проекциями этой плоскости на различные оси.
В [224] было получено иное выражение для масштабной
плоскости:
![]() (значения
(значения ![]() и
и ![]() найдены в цветовой полосе
найдены в цветовой полосе ![]() ). Величины степеней
в этом выражении отличаются от ожидаемых на основе теоремы вириала
при постоянном отношении масса-светимость (2 и -1 соответственно),
однако согласуются с теми, что ожидаются из найденного в [224]
соотношения Талли-Фишера:
). Величины степеней
в этом выражении отличаются от ожидаемых на основе теоремы вириала
при постоянном отношении масса-светимость (2 и -1 соответственно),
однако согласуются с теми, что ожидаются из найденного в [224]
соотношения Талли-Фишера:
![]() .
С другой стороны, такая же масштабная плоскость предсказывается
моделью формирования диска, описанной ранее. Действительно,
из формул (86-87)
следует, что
.
С другой стороны, такая же масштабная плоскость предсказывается
моделью формирования диска, описанной ранее. Действительно,
из формул (86-87)
следует, что
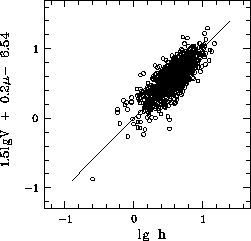
![]() . На рис. 44 показано,
что данные для дисков спиральных галактик удовлетворяют этому
соотношению (разброс lg
. На рис. 44 показано,
что данные для дисков спиральных галактик удовлетворяют этому
соотношению (разброс lg![]() составляет 0.13). Диаграмма
составляет 0.13). Диаграмма ![]() -
-![]() ,
рассмотренная нами ранее, является одной из проекций этой
масштабной плоскости и она также согласуется с моделью [197].
,
рассмотренная нами ранее, является одной из проекций этой
масштабной плоскости и она также согласуется с моделью [197].
<< 8. Некоторые результаты фотометри... | Оглавление | 8.2 Эллиптические галактики >>
|
Публикации с ключевыми словами:
Фотометрическая система - слабые галактики - Скопление галактик - фотометрия
Публикации со словами: Фотометрическая система - слабые галактики - Скопление галактик - фотометрия | |
См. также:
Все публикации на ту же тему >> | |