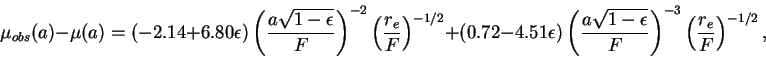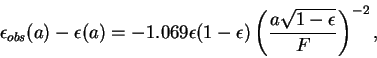<< 2.1 Основные этапы ... | Оглавление | 2.3 Стандартные пакеты программ >>
2.2 Проблемы и точность
На точность поверхностной фотометрии влияет множество факторов. Одни из них приводят к смещению нуль-пункта шкалы звездных величин, другие перераспределяют энергию в фокальной плоскости телескопа и, следовательно, изменяют распределение поверхностной яркости, третьи просто вносят случайные ошибки. Далее мы рассмотрим только три наиболее существенных из них. Подробное обсуждение различных источников ошибок в фотометрии галактик можно найти, например, в статьях [19,20,23,31,32].
2.2.1 Фон неба
Наиболее серьезной проблемой в фотометрии протяженных объектов является то, что галактики наблюдаются на фоне ночного неба, излучение которого дает заметный вклад в распределение яркости изучаемых объектов (особенно в их слабых периферийных областях) [20]. Фон неба влияет также на обнаружение галактик, на точность измерения их звездных величин и показателей цвета.
Основной вклад в яркость безлунного ночного неба дают следующие составляющие:
- --- свечение атмосферы, обусловленное фотохимическими процессами в ее верхних слоях;
- --- зодиакальный свет -- рассеянное на межпланетной пыли излучение Солнца;
- --- излучение слабых и неразрешенных звезд нашей Галактики;
- --- диффузное излучение от далеких, слабых галактик.
Другие факторы, влияние которых на яркость фона неба заметно меньше, --
это вариации межзвездного поглощения в Галактике; слабые отражательные и
эмиссионные туманности Галактики; протяженные ореолы от ярких звезд,
расположенных вблизи наблюдаемых объектов (импульсные отклики
(PSF -- см. п. 2.2.2)
таких звезд могут прослеживаться до
![]() ).
).
Относительный вклад этих составляющих в общую яркость неба
варьируется в зависимости от положения наблюдателя на Земле. Он
зависит также от галактических и эклиптических координат
наблюдаемого объекта. Согласно [33] основной вклад
в наблюдаемый фон неба (при наблюдениях в зените, без Луны,
вдали от плоскостей эклиптики и Млечного Пути, а также
в минимуме солнечной активности)
вносят свечение атмосферы (![]() 2/3) и зодиакальный свет
(
2/3) и зодиакальный свет
(![]() 1/3).
Свечение атмосферы изменяется на масштабах времени 2-3 минуты и оно
приводит к вариациям среднего уровня фона неба в пределах
1/3).
Свечение атмосферы изменяется на масштабах времени 2-3 минуты и оно
приводит к вариациям среднего уровня фона неба в пределах
![]() 2% [20].
Кроме того, свечение атмосферы зависит от фазы цикла солнечной
активности (эти вариации могут достигать фактора 4-5 [34]).
2% [20].
Кроме того, свечение атмосферы зависит от фазы цикла солнечной
активности (эти вариации могут достигать фактора 4-5 [34]).
В безлунные ясные ночи поверхностная яркость фона неба в зените
в местах с хорошим астроклиматом в цветовой полосе ![]() составляет
составляет
![]() =22.5-23.0 [33,34,35].
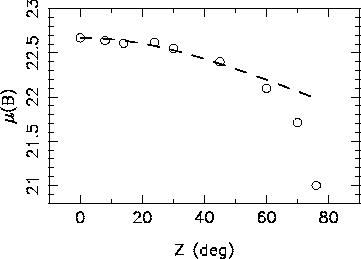
С удалением от зенита яркость фона увеличивается. Этот рост может быть
описан следующей приближенной формулой [36]:
=22.5-23.0 [33,34,35].
С удалением от зенита яркость фона увеличивается. Этот рост может быть
описан следующей приближенной формулой [36]:
![]() , где
, где ![]() и
и ![]() -- это поверхностные
яркости фона неба в зените и в точке наблюдений, а
-- это поверхностные
яркости фона неба в зените и в точке наблюдений, а ![]() -- соответствующее
зенитное расстояние в радианах (см. рис. 2). При больших зенитных расстояниях
(
-- соответствующее
зенитное расстояние в радианах (см. рис. 2). При больших зенитных расстояниях
(
![]() ) лучше использовать более точную аппроксимацию
(например, приведенную в [37]). Фон неба является
относительно ``красным'' -- его показатели цвета близки к цветам
эллиптических галактик (
) лучше использовать более точную аппроксимацию
(например, приведенную в [37]). Фон неба является
относительно ``красным'' -- его показатели цвета близки к цветам
эллиптических галактик (
![]() [33,34,35]).
[33,34,35]).
 |
Поверхностная яркость фона неба при наблюдениях на панорамном
приемнике (ПЗС-матрице, фотопластинке) является функцией координат
элемента изображения (пиксела) -- ![]() . Тогда
для нахождения поверхностной яркости галактики в какой-либо точке
необходимо из наблюдаемого (галактика + фон) значения яркости
вычесть значение фона:
. Тогда
для нахождения поверхностной яркости галактики в какой-либо точке
необходимо из наблюдаемого (галактика + фон) значения яркости
вычесть значение фона:
![]() .
Ключевым этапом при этом является определение поверхностной
яркости фона в области, занимаемой галактикой. Как правило, для этого
осуществляется двумерная интерполяция фона, найденного в области
кадра вне исследуемой галактики, в область, занимаемую объектом.
При этом точность интерполяции зависит от соотношения
между площадью, по которой находилось приближение фона, и площадью,
занимаемой галактикой: чем больше отношение этих площадей, тем
точнее можно оценить фон под галактикой. На практике, однако,
выбор свободной от галактики части кадра часто затруднен из-за
небольшого размера самого кадра, перекрытия изображений галактик во
взаимодействующих системах, группах и скоплениях, и из-за возможного
наличия у галактик слабых внешних оболочек.
.
Ключевым этапом при этом является определение поверхностной
яркости фона в области, занимаемой галактикой. Как правило, для этого
осуществляется двумерная интерполяция фона, найденного в области
кадра вне исследуемой галактики, в область, занимаемую объектом.
При этом точность интерполяции зависит от соотношения
между площадью, по которой находилось приближение фона, и площадью,
занимаемой галактикой: чем больше отношение этих площадей, тем
точнее можно оценить фон под галактикой. На практике, однако,
выбор свободной от галактики части кадра часто затруднен из-за
небольшого размера самого кадра, перекрытия изображений галактик во
взаимодействующих системах, группах и скоплениях, и из-за возможного
наличия у галактик слабых внешних оболочек.
Интерполяция фона в область объекта предполагает, что фон распределен
регулярным, предсказуемым образом и, следовательно, его случайные
флуктуации не могут быть учтены. В центральных областях галактик,
где
![]() , вклад этих случайных отклонений
поверхностной яркости пренебрежимо мал. Например, для
, вклад этих случайных отклонений
поверхностной яркости пренебрежимо мал. Например, для
![]() и
и
![]() относительной ошибке фона в области объекта
относительной ошибке фона в области объекта
![]() соответствует
ошибка в звездных величинах 0.
соответствует
ошибка в звездных величинах 0.![]() 001. Однако на периферии галактик,
где
001. Однако на периферии галактик,
где
![]() , вклад ошибок оценки фона
может стать доминирующим. Например, при
, вклад ошибок оценки фона
может стать доминирующим. Например, при
![]() и
и
![]() относительная погрешность фона
относительная погрешность фона
![]() приводит к ошибке
0.
приводит к ошибке
0.![]() 1. Если же
1. Если же
![]() , то ошибка
превышает 1
, то ошибка
превышает 1![]() . (Приведенные выше числовые примеры взяты из
статьи [20].)
. (Приведенные выше числовые примеры взяты из
статьи [20].)
На рис. 3
по аналогии с тем, как это было сделано в [20,26],
мы иллюстрируем влияние неточного учета фона неба на распределение
поверхностной яркости у двух модельных галактик -- эллиптической, задаваемой
законом Вокулера (п. 4.1), и спиральной, распределение поверхностной
яркости у которой описывается экспоненциальным законом (п. 5.1).
Модель эллиптической галактики взята с эффективной поверхностной
яркостью1![]() (как у стандартной эллиптической галактики NGC 3379
согласно [38]), для спиральной галактики значение центральной
поверхностной яркости диска принято равным
(как у стандартной эллиптической галактики NGC 3379
согласно [38]), для спиральной галактики значение центральной
поверхностной яркости диска принято равным
![]() [39].
Значение яркости фона неба для показанных на рис. 2 примеров
составляет
[39].
Значение яркости фона неба для показанных на рис. 2 примеров
составляет
![]() . Оси абсцисс на рис. 2 размечены
в безразмерных единицах: в долях эффективного радиуса
. Оси абсцисс на рис. 2 размечены
в безразмерных единицах: в долях эффективного радиуса ![]() для
эллиптической галактики и в долях экспоненциального масштаба диска
для
эллиптической галактики и в долях экспоненциального масштаба диска ![]() для спиральной галактики.
для спиральной галактики.
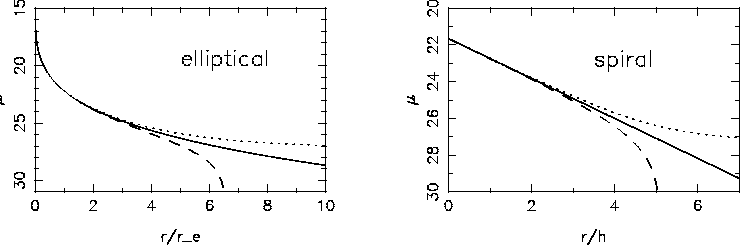 |
Как видно на рис. 3, неточный учет фона неба при фотометрии может привести к сильному искажению периферийных областей галактик: можно легко получить усеченные распределения яркости (штриховые линии), а можно, наоборот, ``открыть'' протяженные оболочки (линии из точек).
Капаччиоли и Вокулер [20] заключили, что статистические
флуктуации фона неба ограничивают область относительно точной
наземной поверхностной фотометрии галактик уровнем яркости ![]() (или
(или ![]() 0.4
0.4 ![]() /пк
/пк![]() ). Этот предел не может быть
сильно понижен и при наблюдениях из космоса, так как при этом
исключается только первая из перечисленных ранее составляющих
фона (свечение верхних слоев атмосферы).
). Этот предел не может быть
сильно понижен и при наблюдениях из космоса, так как при этом
исключается только первая из перечисленных ранее составляющих
фона (свечение верхних слоев атмосферы).
В наиболее тщательных наземных фотометрических исследованиях
галактики, действительно, прослеживаются до
![]() (например, [38]).
В работе [32] для фотометрии спиральной галактики NGC 5907
были использованы среднеполосные фильтры, выбранные так, чтобы
в них не попали наиболее интенсивные и переменные линии излучения
ночного неба (центральные длины волн фильтров равны 6660Å и
8020Å, ширины -- 480Å и 260Å соответственно).
Это позволило авторам учесть вклад фона с точностью
(например, [38]).
В работе [32] для фотометрии спиральной галактики NGC 5907
были использованы среднеполосные фильтры, выбранные так, чтобы
в них не попали наиболее интенсивные и переменные линии излучения
ночного неба (центральные длины волн фильтров равны 6660Å и
8020Å, ширины -- 480Å и 260Å соответственно).
Это позволило авторам учесть вклад фона с точностью
![]() 0.05% и проследить распределение яркости у галактики вплоть
до
0.05% и проследить распределение яркости у галактики вплоть
до ![]() (или до
(или до ![]() ) с ошибкой
) с ошибкой ![]() 1
1![]() .
Наблюдения на Космическом Телескопе (КТ) имени Хаббла с помощью
WFPC2 за несколько часов экспозиции также позволяют изучить
галактики до примерно такого же предела [40].
.
Наблюдения на Космическом Телескопе (КТ) имени Хаббла с помощью
WFPC2 за несколько часов экспозиции также позволяют изучить
галактики до примерно такого же предела [40].
2.2.2 PSF
Наблюдаемое в фокальной плоскости телескопа изображение объекта искажено совместным влиянием атмосферы и оптической системы. Нестабильность оптических свойств атмосферы приводит к тому, что изображение точечного источника (например, звезды) является неустойчивым турбулентным диском. Кроме того, подобное же ``размытие'' изображения производится и телескопической системой, поскольку она всегда обладает остаточными сферическими аберрациями, вызванными ошибками в изготовлении оптики и температурными деформациями зеркал. Неточности гидировки и дефокусировка также ухудшают изображения.
Предположив, что все эти искажения являются линейными и пространственно
инвариантными, связь наблюдаемого (![]() ) и истинного (
) и истинного (![]() )
изображений объекта можно представить следующим образом:
)
изображений объекта можно представить следующим образом:
![]() ,
где функция
,
где функция ![]() называется импульсной характеристикой искажающей
системы (в нашем случае такой системой является атмосфера+телескоп)
или передаточной функцией. В англоязычной литературе для названия
называется импульсной характеристикой искажающей
системы (в нашем случае такой системой является атмосфера+телескоп)
или передаточной функцией. В англоязычной литературе для названия
![]() часто используется аббревиатура PSF (point spread function -
функция рассеяния точки). В качестве экспериментальной реализации
PSF в астрономии обычно используют профили звездных изображений.
Как правило, в качестве аналитической аппроксимации PSF
рассматривают гауссиану и ее различные модификации
(например, гауссиана с экспоненциальными крыльями, суперпозиция
нескольких гауссиан). В пакете программ
IRAF (см. далее п. 2.3) в качестве ``стандартной'' PSF применяется
функция Моффата (Moffat function) [41]:
часто используется аббревиатура PSF (point spread function -
функция рассеяния точки). В качестве экспериментальной реализации
PSF в астрономии обычно используют профили звездных изображений.
Как правило, в качестве аналитической аппроксимации PSF
рассматривают гауссиану и ее различные модификации
(например, гауссиана с экспоненциальными крыльями, суперпозиция
нескольких гауссиан). В пакете программ
IRAF (см. далее п. 2.3) в качестве ``стандартной'' PSF применяется
функция Моффата (Moffat function) [41]:
![]() , где параметр
, где параметр ![]() характеризует ширину PSF, а
характеризует ширину PSF, а ![]() -- константа (обычно используются значения
-- константа (обычно используются значения
![]() ).
).
``Размытие'' изображения может существенно повлиять на распределение поверхностной яркости в центральных областях галактик. Особенно сильно оно сказывается на далеких объектах, размеры которых сравнимы с шириной PSF. К примеру, наземные и космические исследования подстилающих галактик квазаров, изучение Фундаментальной Плоскости для галактик ранних типов (см. п. 8.2) -- эти работы невозможны без тщательного учета влияния PSF на фотометрические характеристики объектов (например, [42,43]).
Влияние PSF (или ``качества изображения'') искажает измерения видимых
звездных величин (![]() ) и поверхностных яркостей
вблизи от ядра галактики, приводит к увеличению
эффективного радиуса
) и поверхностных яркостей
вблизи от ядра галактики, приводит к увеличению
эффективного радиуса ![]() , а также к уменьшению видимой эллиптичности изофот
(
, а также к уменьшению видимой эллиптичности изофот
(
![]() , где
, где ![]() и
и ![]() -- это большая и малая полуоси
аппроксимирующего данную изофоту эллипса).
Для описания этого эффекта было предложено несколько аналитических
выражений. Например, Паре [42] были предложены
следующие формулы для коррекции наблюдений эллиптических галактик
(а также описываемых законом Вокулера балджей спиральных галактик):
-- это большая и малая полуоси
аппроксимирующего данную изофоту эллипса).
Для описания этого эффекта было предложено несколько аналитических
выражений. Например, Паре [42] были предложены
следующие формулы для коррекции наблюдений эллиптических галактик
(а также описываемых законом Вокулера балджей спиральных галактик):
где
| ( |
( |
( |
|
| 2 | -0.445 | -0.199 | -0.081 |
| 3 | -0.211 | -0.094 | -0.039 |
| 4 | -0.123 | -0.055 | -0.022 |
| 5 | -0.080 | -0.036 | -0.015 |
| 10 | -0.021 | -0.009 | -0.004 |
|
|
|
|
|
| ( |
( |
( |
|
| 1.1 | -0.177 | -0.353 | -0.618 |
| 2 | -0.053 | -0.107 | -0.187 |
| 3 | -0.024 | -0.048 | -0.083 |
| 4 | -0.013 | -0.027 | -0.047 |
| 5 | -0.009 | -0.017 | -0.030 |
| ( |
( |
( |
|
| 1 | 0.334 | 0.302 | 0.270 |
| 2 | 0.083 | 0.075 | 0.067 |
| 3 | 0.037 | 0.034 | 0.030 |
| 4 | 0.021 | 0.019 | 0.017 |
| 5 | 0.013 | 0.012 | 0.011 |
В таблицах 1-3
приведены результаты расчетов по формулам (3-5).
Очевидно, что, когда рассматривается центральная область галактики,
сравнимая с шириной PSF, ``качество изображения'' очень сильно
влияет на ее наблюдаемые характеристики. Например, если стандартная
эллиптическая галактика NGC 3379 будет находится на умеренном
красном смещении ![]() , то при значениях параметра замедления
, то при значениях параметра замедления
![]() и постоянной Хаббла H
и постоянной Хаббла H![]() =65 км/с/Мпк ее эффективному
радиусу
=65 км/с/Мпк ее эффективному
радиусу ![]() кпк [38] будет соответствовать угловой
размер 0.
кпк [38] будет соответствовать угловой
размер 0.![]() 5. Предположим, что мы наблюдаем эту галактику в месте
с очень хорошим ``качеством изображения'' -- F=FWHM
5. Предположим, что мы наблюдаем эту галактику в месте
с очень хорошим ``качеством изображения'' -- F=FWHM![]() =0.
=0.![]() 5.
Тогда, при измерении с круглой диафрагмой диаметром 1.
5.
Тогда, при измерении с круглой диафрагмой диаметром 1.![]() 0, мы
недооценим ее видимую звездную величину на 0.
0, мы
недооценим ее видимую звездную величину на 0.![]() 33. Значение
поверхностной яркости на расстоянии 1.
33. Значение
поверхностной яркости на расстоянии 1.![]() 0 (или 5.5 кпк) от ядра галактики
будет занижено на 0.
0 (или 5.5 кпк) от ядра галактики
будет занижено на 0.![]() 45. В пределах 0.
45. В пределах 0.![]() 5 от ядра изофоты
галактики будут круглыми.
5 от ядра изофоты
галактики будут круглыми.
В [47] приведено общее аналитическое исследование задачи об
исправлении характеристик распределения яркости, описываемого формулой
Серсика (см. далее п. 4.2), за влияние PSF, представленной гауссианой.
Решение задачи представлено в виде разложений по гипергеометрическим
функциям. Оказалось, что атмосферное размытие в наибольшей степени влияет
на параметр ![]() (формула (25)), характеризующий форму
распределения яркости.
(формула (25)), характеризующий форму
распределения яркости.
2.2.3 Нуль-пункт шкалы звездных величин
Нуль-пункт шкалы звездных величин обычно устанавливается по
наблюдениям фотометрических стандартов -- звезд с хорошо известными
видимыми звездными величинами (с ошибкой ![]() ),
например, из списка Ландольта [48].
Звезды наблюдаются несколько раз в течении данной
ночи и по их наблюдениям строятся соотношения между инструментальными
звездными величинами и величинами в стандартной системе [49].
Если инструментальная и стандартная (например,
),
например, из списка Ландольта [48].
Звезды наблюдаются несколько раз в течении данной
ночи и по их наблюдениям строятся соотношения между инструментальными
звездными величинами и величинами в стандартной системе [49].
Если инструментальная и стандартная (например, ![]() -система Джонсона
и Моргана) системы близки, то связь между ними может быть представлена
в виде линейных уравнений:
-система Джонсона
и Моргана) системы близки, то связь между ними может быть представлена
в виде линейных уравнений:
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ,
, ![]() и
и ![]() -- внеатмосферные величины звезд в инструментальной
системе, а
-- внеатмосферные величины звезд в инструментальной
системе, а ![]() ,
, ![]() ,
, ![]() -- соответствующие им величины в
стандартной. В идеальном случае, то есть тогда, когда системы совпадают,
-- соответствующие им величины в
стандартной. В идеальном случае, то есть тогда, когда системы совпадают,
![]() и
и ![]() . Внеатмосферная инструментальная звездная
величина (например,
. Внеатмосферная инструментальная звездная
величина (например, ![]() ) обычно записывается так:
) обычно записывается так:
![]() ,
,
где ![]() -- суммарная относительная яркость звезды,
-- суммарная относительная яркость звезды, ![]() --
продолжительность экспозиции,
--
продолжительность экспозиции, ![]() -- коэффициент атмосферной
экстинкции (поглощения) в данной цветовой полосе и
-- коэффициент атмосферной
экстинкции (поглощения) в данной цветовой полосе и ![]() -- воздушная
масса. Для не очень больших значений зенитного расстояния
-- воздушная
масса. Для не очень больших значений зенитного расстояния ![]() (
(
![]() ) можно считать, что
) можно считать, что
![]() .
На практике при обработке наблюдений часто используют
средние значения коэффициентов поглощения
.
На практике при обработке наблюдений часто используют
средние значения коэффициентов поглощения ![]() , которые, как правило,
уже известны для многих обсерваторий по результатам выполненных
ранее наблюдений. Процедура точного определения коэффициентов
экстинции подробно описана в статье Харди [49].
, которые, как правило,
уже известны для многих обсерваторий по результатам выполненных
ранее наблюдений. Процедура точного определения коэффициентов
экстинции подробно описана в статье Харди [49].
При выборе звезд-стандартов желательно,
чтобы диапазон изменения их показателей цвета соответствовал или
перекрывал диапазон изменения показателей цвета наблюдающихся
в течение данной ночи галактик. При тщательных наблюдениях и измерениях
точность нуль-пункта шкалы звездных величин по наблюдениям стандартов
может быть не хуже ![]() .
.
Другой распространенный способ стандартизации фотометрических данных - это привязка к фотоэлектрическим измерениям исследуемой галактики, выполненным с использованием диафрагм разного размера (как правило, диафрагмы центрируются на ядро). В этом случае на точность нуль-пункта влияет погрешность фотоэлектрических измерений, а также точность выставления измерительной диафрагмы на ядро. В случае неаккуратного центрирования ошибка нуль-пункта шкалы звездных величин зависит от относительной величины смещения диафрагмы, а также от закона распределения поверхностной яркости в галактике и от величины характерного масштаба этого распределения. Величины ошибок центрирования для модели эллиптической галактики приведены на рис. 2 в статье [20]. В случае аккуратного выставления диафрагм ошибки центрирования не превышают нескольких сотых звездной величины.
Для привязки ПЗС и фотографических данных удобно использовать каталог Лонго и Вокулера [50], суммирующий результаты фотоэлектрических наблюдений для нескольких тысяч галактик. Кроме того, результаты оригинальных фотоэлектрических наблюдений и соответствующие ссылки можно найти в базах внегалактических данных - например, в NED (NASA/IPAC Extragalactic Database -- см. http://nedwww.ipac.caltech.edu) [51] или Hypercat (http://www-obs.univ-lyon1.fr/hypercat) [52].
Среди других способов стандартизации поверхностной фотометрии можно отметить привязку к фотоэлектрическим измерениям фона неба вблизи от исследуемого объекта [53], а также к фотоэлектрическим сканам галактики.
<< 2.1 Основные этапы поверхностной | Оглавление | 2.3 Стандартные пакеты ... >>
|
Публикации с ключевыми словами:
Фотометрическая система - слабые галактики - Скопление галактик - фотометрия
Публикации со словами: Фотометрическая система - слабые галактики - Скопление галактик - фотометрия | |
См. также:
Все публикации на ту же тему >> | |