Астронет > Размерности и подобие астрофизических величин

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Размерности и подобие астрофизических величин << § 8.1 Структура квазаров и ядер галактик | Оглавление | § 8.3 Основные параметры Метагалактики >>

§ 8.2 Гравитационная неустойчивость

Возникновение звезд и других небесных тел возможно только потому, что в мире существует гравитация. Об этом, писал еще Ньютон в письме к Бентли в 1692 г. Идея Ньютона была оформлена физически и математически Джинсом в его известной книге "Астрономия и космогония" [10]. Сущность механизма Ньютона-Джинса, или механизма гравитационной неустойчивости, заключается в следующем.

Во всяком газе всегда имеются флуктуации плотности, возникающие при хаотическом, движении составляющих газ атомов или молекул. Эти флуктуации воникают и распадаются, причем динамика флуктуации определяется одним параметром - температурой.

Ситуация существенно изменится, если мы, кроме температуры, рассмотрим, другой фактор - тяготение. Для малых масштабов гравитация не существенна. Для больших масштабов может случиться, что собственное притяжение такой флуктуации окажется способные удержать газ в данном объеме и не дать ему рассеяться. Сила тяготения нарастает с увеличением массы, а тепловые свойства среды не зависят от размера. В этих условиях возможно разбиение первоначально однородной среды на сгустки с некоторым характерным масштабом, называемым джинсовской длиной.

Оценку джинсовской, или критической, длины можно сделать следующим образом. Сравним тепловую энергию сгущения (флуктуации) с его гравитационной энергией. Гравитационная энергия на единицу массы

$F_g \approx \frac{GM}{\lambda} \approx G\rho\lambda^2,$ (8.12)

где λ - характерный размер сгущения. Тепловая энергия на единицу массы есть

$E_T \approx \frac{\Re T}{\mu}.$ (8.13)

Приравнивая эти две величины, получим выражение для критической длины волны

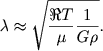
$\lambda \approx \sqrt{\frac{\Re T}{\mu}\frac{1}{G\rho}}.$ (8.14)

Можно получить формулу Джинса и из соображений размерности. Определяющие параметры задачи таковы. Гравитационные свойства среды задаются средней плотностью ρ и постоянной тяготения G. Тепловые свойства зависят от температуры, универсальной газовой постоянной и молекулярного веса. Эти факторы мы сгруппируем вместе. Тогда имеем матрицу размерности:

$\begin{matrix} \, & [\lambda] & [G] & [\rho] & [\frac{\Re T}{\mu}] \\ \mbox{г}&0&-1&1&0 \\ \mbox{см}&1&3&-3&2 \\ \mbox{сек}&0&-2&0&-2 \end{matrix}$

Решение матрицы дает единственный безразмерный комплекс, также приводящий к формуле (8.14) с точностью до некоторого безразмерного множителя. Обычно выражают температуру через изотермическую скорость звука:

$v^2_s = \frac{\Re T}{\mu}.$ (8.15)

Безразмерная постоянная равна π^½, и мы получаем, формулу Джинса в ее обычном виде:

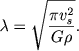
$\lambda = \sqrt{\frac{\pi v_s^2}{G\rho}}.$ (8.16)

Понятие гравитационной неустойчивости имеет простой физический смысл. Устойчивость любой системы проверяется наложением на систему малых колебаний. Если колебания затухают, система устойчива, если они начинают расти - неустойчива. Ввиду наличия гравитации колебания газа в больших масштабах называют "тяжелым звуком" (см. гл. 7). Колебания с меньшей длиной волны затухают, так как в них тепловая энергия больше гравитационной; колебания с большей длиной волны - неустойчивы. Переход среды из устойчивого состояния в неустойчивое легко понять, если вспомнить, что при малых плотностях космический газ почти всегда прозрачен. При постепенном остывании температура понижается и среда становится гравитационно неустойчивой.

В соотношениях (8.14) - (8.16) не рассматривается динамика распада на сгущения, а находится только критерии гравитационной неустойчивости, строго справедливые для случая, когда исходная среда в начальный момент времени покоится. Такая важная для космологии задача, как распад на сгущения расширяющейся среды, была решена впервые Е. М. Лифшицем (подробности см. [2]), который учел зависимость начальной плотности от времени. Впрочем, оказалось, что результаты Джинса с очень небольшими поправками остаются справедливыми и в этом случае, если принимать для $\bar\rho$ мгновенное значение плотности в момент распада среды.

Теперь проследим дальнейшую судьбу гравитационных конфигураций. Массы конденсаций, "образующихся в тяжелом звуке, порядка

$M \approx \rho\lambda^3 \approx \left(\frac{\pi}{G}\right)^{3/2}\frac{v_s^3}{\rho^{1/2}},$ (8.17)

где v_s - характерная скорость. В простейшем случае это скорость звука, но вообще она может отражать и наличие других факторов (вращение, турбулентность, скорость альвеновоких волн). Минимальное значение М определяется газовым и лучистым давлением. Поэтому минимальная масса конденсаций

$M \approx \rho\lambda^3 \approx \left(\frac{\pi}{G}\right)^{3/2}\frac{v_s^3}{\rho^{1/2}},$ (8.18)

В настоящее время минимальная температура космической среды равна 3њ. В прошлом температуры были выше. В зависимости от хода изменения плотности и температуры для конкретных моделей, массы образующихся конденсаций оказываются различными. Конденсации в волнах "тяжелого звука" собирают вещество, оставшееся вне сгущения. Характерное время такого собирания можно оценить, подставляя в формулу аккреции (2.30) вместо массы звезды массу образовавшихся сгущений (8.17). Тогда для относительного изменения массы имеем

$\frac{1}{M}\frac{dM}{dt} \approx (2\pi)^{5/2}(G\rho)^{1/2}.$

Характерное время здесь сравнимо (несколько меньше) со временем, свободного падения. Таким образом, образовавшиеся конденсации быстро собирают большую часть "неиспользованной массы" и затем начинают сжиматься, образуя протозвезды, протогалактики и т.д.

Отметим еще одно обстоятельство. В формуле Джинса нет какой-либо фундаментальной длины, определяемой атомными или какими-либо другими константами. Поэтому, если имеется непрерывный ряд изменения начальных параметров среды - плотности и температуры-мы получим сплошной спектр длин волн неустойчивости. Не исключено, что непрерывный ряд характерных размеров небесных тел - звездных скоплений, галактик, скоплений галактик - есть свидетельство того, что в прошлом во Вселенной имел место процесс гравитационной конденсации.

Обсудим теперь, после выяснения общего физического смысла механизма гравитационной неустойчивости, некоторые дополнительные соображения. Рассмотрим плоскую систему, например, вращающуюся галактику. В этом случае вместо объемной плотности мы должны ввести поверхностную плотность массы

$[\rho_s] = \mbox{г} \cdot \mbox{см}^{-2}.$

В этом случае критерий Джинса приобретает вид

$\lambda = 2\pi\frac{v_s^2}{G\rho_s}.$ (8.19)

Эта формула получена Леду [11]. Здесь λ - толщина гравитационно-устойчивого слоя или диска. Этой формулой можно объяснить известный из радионаблюдений факт утолщения газового диска Галактики от центра к периферии. Толщина диска связана с плотностью, и по мере убывания плотности к периферии толщина диска растет.

Далее, если образующиеся сгущения вращаются, например из-за несимметричности в начальный момент, то при сжатии угловая скорость увеличивается в соответствии с теоремой сохранения углового момента. Тогда условие, требующее, чтобы сгущение не разлетелось из-за вращения, имеет вид

$G\rho \lesssim (\Delta\Omega)^2,$ (8.20)

где ΔΩ;;; - изменение угловой скорости в пределах рассматриваемого сгущения.

Вопрос о вращении конденсаций (протогалактик) можно рассмотреть с другой стороны. Пусть мы имеем выделившуюся в результате джинсовской неустойчивости конденсацию с вращением. Она характеризуется следующими параметрами: массой, вращательным моментом, постоянной тяготения (конденсация гравитационно связана), и температурой, которую будем выражать через скорость звука. Найдем зависимость между этими факторами. Матрица размерности

$\begin{matrix} \, & [v_s] & [\mathfrak{M}] & [G] & [M] \\ \mbox{г}&0&1&-1&1 \\ \mbox{см}&1&2&3&0 \\ \mbox{сек}&-1&-1&-2&0 \end{matrix}$

дает единственный безразмерный комплекс, откуда следует формула

$\mathfrak{M} = const \cdot \frac{GM^2}{v_2}$ (8.21)

Постоянная согласно [12] равна 12/5 π . Аналогичная формула для релятивистского диска $\mathfrak{M} \approx \frac{GM^2}{c}$ была выведена Вагонером [13]. Как уже отмечалось в гл. 7, наблюдательные данные лучше всего соответствуют зависимости $\mathfrak{M} \sim M^{7/4}$ . Другие авторы получали близкие зависимости $\mathfrak{M} \sim M^{2}$ и $\mathfrak{M} \sim M^{5/3}$ (см. [14]), так что можно считать соотношение (8.21)) приближенно верным.

Итак, если галактика "помнит" начальные условия своего образования и зависимость $\mathfrak{M} \sim M^2$ можно рассматривать как результат гравитационной неустойчивости, то можно сделать попытку оценить температуру среды, из которой образовались галактики. Пусть в некоторой достаточно близкой окрестности нашего Млечного Пути температура и тем самым величина bj одинаковы. Численный коэффициент зависимости $\mathfrak{M}$ от М можно определить из наблюдений (см. рис. 26). Тогда из (8.21) находим v_s ≈ 3,5 ⋅ 10⁶ см/сек. Если эта скорость есть обычная скорость, то Т ≈ 10⁶ К. Эту величину можно, по-видимому, рассматривать как определенную из наблюдений.

Обсудим теперь эффекты магнитного поля. Магнитное поле, как и упомянутое ранее вращение, фактор существенно анизотропный. Магнитное поле препятствует сжатию в направлении, перпендикулярном к силовым линиям. Вдоль этих линий поле не только не препятствует сжатию, но и способствует ему (неустойчивость Пикельнера - Паркера).

Для количественных оценок можно считать характерной скоростью скорость альвеновских волн

$v_A = \frac{H}{\sqrt{4\pi \rho}}$ (8.22)

или сравнивать гравитационное и магнитное давления

$G\rho^2\lambda^2 \approx \frac{H^2}{8\pi}.$ (8.23)

На ранних стадиях эволюции Вселенной магнитное давление может превосходить давление газа, и в этих условиях влияние магнитного поля на процесс образования галактик может оказаться существенным. Хотя наблюдательные данные по далеким радиогалактикам еще не дают однозначных выводов о наличии и величине поля, его существование в принципе не исключено. В частности, магнитное поле могло бы объяснить любопытный факт выстраивания галактик цепочками. В этом случае естественно предполагать гравитационную неустойчивость некоторой цилиндрической конфигурации, образовавшейся под действием магнитного поля. Гравитационная неустойчивость космологических моделей с первичным магнитным полем, приводящая к образованию дисковых (двумерных) и нитевидных (одномерных) образований, рассматривалась в работе [15].

Итак, в общем случае для сгущения, выделившегося из первично однородной среды благодаря механизму гравитационной неустойчивости, можно записать условие равновесия

$G\rho^2\lambda^2 \approx \rho(v_R^2 + \langle v \rangle^2) + \frac{H^2}{8\pi} + p_{\mbox{газ}} + p_{\mbox{луч}},$ (8.24)

где v_R - вращательная скорость, 〈v〉 - турбулентная скорость. В такой формулировке условие равновесия (8.24), как можно видеть, эквивалентно известной теореме вириала.

<< § 8.1 Структура квазаров и ядер галактик | Оглавление | § 8.3 Основные параметры Метагалактики >>

Мнения читателей [4]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце