Глава V. Стационарные движения в звездах
Общеизвестно высказывание Эддигтона о том, что "нет ничего проще звезды". Однако если это и справедливо, то только до тех пор, пока мы не рассматриваем движения в звездах. Учет вращения и магнитных полей сразу вносит существенный элемент неопределенности в теорию, поскольку распределение скоростей вращения и напряженности магнитных полей внутри звезды остается не известным. Несколько лучше обстоит дело с теорией пульсаций звезд, где можно считать понятными основные черты явления. При исследовании движений в звездах часто трудно получить более или менее полные уравнения, которые можно было бы решить однозначно. Здесь соображения теории размерностей иногда остаются единственно возможными.
В настоящей главе мы рассмотрим с точки зрения теории размерностей и подобия стационарные движения - пульсации звезд, их вращения и магнитные поля, а также условия конвекции и турбулентности в звездах, межзвездном пространстве и атмосферах планет. В следующей главе мы рассмотрим нестационарные движения автомодельного типа в звездах и межзвездном пространстве.
§ 5.1 Пульсация переменных звезд
Звездные пульсации, т. е. периодические сжатия и расширения звезд с относительно небольшой амплитудой, очень подробно исследовались различными астрофизическими методами (см. сборник статей [1]). Очень много работ было посвящено и теоретической интерпретации этого явления. Можно отметить книгу Росселанда [2], статьи С. А. Жевакина в сборнике [1] и его обзор [3], а также статьи Беккера, Кокса и Кристи в сборнике [4] и Кристи в сборнике [5].
В настоящее время теоретический анализ явления звездной переменности основан почти исключительно на численных расчетах. Но поскольку основная наша цель - нахождение критериев подобия в астрофизических явлениях, то мы рассмотрим здесь, хотя и приближенно, но зато с достаточной общностью, аналитическое решение задачи о вычислении параметров звездных пульсаций.
Уравнения структуры стационарных звезд, записанные в предыдущей главе, не учитывают движений газа. Внесем теперь в эти уравнения члены, описывающие радиальные пульсации звезд. Общая теория учитывает и нерадиальные пульсации, однако мы это делать не будем.
Уравнения пульсации звезд удобнее записывать в лагранжевой системе координат, рассматривая в качестве независимой переменной не радиус r, а массу, заключенную внутри сферы радиуса r, т. е. величину, обозначенную раньше через М(r), а теперь обозначаемую через Мr. В лагранжевой системе координат положение данного элемента массы газа есть r(Мr, t), т. е. является функцией массы внутри сферы r и времени t как независимых переменных. Из условия непрерывности следует первое уравнение:
|
|
(5.1) |
Уравнение движения элемента массы под действием как гравитационной силы, так и градиента давления, имеет вид
|
|
(5.2) |
или, в лагранжевых переменных,
|
|
(5.3) |
Уравнение лучистой теплопроводности в лагранжевых переменных запишется в виде
|
|
(5.4) |
Здесь Lr - количество энергии, генерируемое за секунду внутри сферы радиуса r, или, иными словами, в области, занятой массой Мr. Температура, как и другие параметры, зависит от Мr и t.
В уравнении генерации энергии теперь нужно учесть и изменение тепловой энергии со временем при пульсациях, а также работу, совершаемую при сжатиях и разрежениях. В лагранжевых координатах это уравнение имеет вид
|
|
(5.5) |
где ε - по-прежнему, мощность энергии, выделяемой в одном грамме вещества при термоядерных реакциях, cvT - внутренняя энергия единицы массы газа. Теплоемкость при постоянном объеме cv может быть записана через характерный показатель адиабаты для смеси газа и излучения Γ:
|
|
(5.6) |
где Γ есть функция β - отношения газового давления к полному:
|
|
(5.7) |
С условием (5.6) уравнение (5.5) принимает вид
|
|
(5.8) |
Здесь под ∂/∂ t - следует, вообще говоря, понимать полную производную по времени, т. е. с учетом и члена ![]() , где v - скорость.
, где v - скорость.
Система уравнений (5.1), (5.3), (5.4) и (5.8) совместно с определением функций ϰ , ε и μ , представляет собой полную систему уравнений радиальных звездных пульсаций. Мы примем для этих функций степенные зависимости, введенные в предыдущей главе.
Здесь нужно сделать одно существенное замечание. В реальных пульсирующих звездах наибольшие колебания происходят во внешних слоях звезд, в частности, в зонах ионизации водорода и гелия. Там коэффициент непрозрачности ведет себя очень сложным образом, и любая степенная зависимость оказывается недостаточно точной. Поэтому анализ, основанный на степенном представлении коэффициента непрозрачности (что необходимо для применения метода подобия), может рассматриваться лишь как качественно правильный. Более или менее точная количественная теория звездных пульсаций может быть построена только на основе численного моделирования с учетом табличных данных для коэффициента непрозрачности. Краткое описание численного моделирования пульсаций мы приведем ниже.
Возвратимся к системе уравнений, записанной выше, и перейдем в ней к безразмерным переменным, введенным в предыдущей главе, а именно:
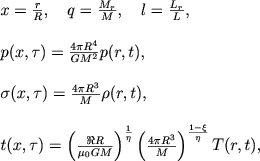
|
(5.9) |
где t(х, τ) - безразмерная температура. Кроме того, введем безразмерное время по формуле
|
|
(5.10) |
где t - размерное время. Система уравнений пульсаций в безразмерном виде запишется так (теперь q и τ есть независимые переменные):
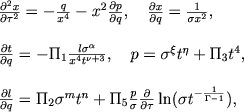
|
(5.11) |
где Π1, Π2, Π3 - безразмерные комплексы, определенные в предыдущей главе:
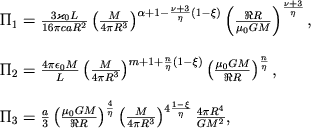
|
(5.12) |
а Π5 есть новый безразмерный комплекс:
|
|
(5.13) |
Пульсации звезд, как правило, малы по амплитуде. Наибольшая величина амплитуды пульсаций, достигаемая у поверхности звезды, редко превышает 5%. В глубоких слоях звезды амплитуда пульсаций порядка 10-3. Хотя пульсации не всегда можно считать линейными, но в первом приближении мы ограничимся линейной задачей. Попутно отметим, что частный случай нелинейных, но адиабатических пульсаций газового шара, допускающий аналитическое решение, был указан Л. И. Седовым.
Линеаризуем систему уравнений (5.11). Для этого произведем замену искомых функций p → p(1+p'), x → x(1+x')... и т. д., где штрихованные величины есть безразмерные функции аргументов q и τ, а нештрихованные зависят только от q и описывают стационарное равновесное состояние. Будем считать, что все штрихованные величины много меньше единицы. В нулевом приближении нештрихованные величины удовлетворяют уравнениям равновесия, а в следующем, первом приближении получаем линейные уравнения для штрихованных величин:
![$$
\begin{array}{l}
\frac{\partial p'}{\partial q} + \frac{1}{xp}\frac{\partial^2 p'}{\partial \tau^2} = \frac{q}{x^4p}(p' + 4x'), \\ \\
\frac{\partial x'}{\partial q} = -\frac{\sigma' + 3x'}{x^3\sigma}, \\ \\
\frac{\partial t'}{\partial q} = -\Pi_1 \frac{l\sigma^{\alpha}}{x^4t^{\nu+4}}[l' + \alpha\sigma' - (\nu + 4)t' - 4x'], \\ \\
\frac{\partial l'}{\partial q} = \Pi_2 \frac{\sigma^mt^n}{l}(m\sigma' + nt' - t) + \Pi_5\frac{p}{\sigma l}\left(\frac{\partial \sigma'}{\partial \tau} - \frac{1}{\Gamma - 1}\frac{\partial t'}{\partial \tau}\right), \\ \\
p' = \frac{\sigma^\xi t^\eta}{p}(\xi\sigma' + \eta t') + 4\Pi_3\frac{t^4}{p}t'.
\end{array}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula64.gif)
|
(5.14) |
В этой системе уравнений нештрихованные величины определяются системой уравнений (4.59), которую можно переписать в координатах Лагранжа:
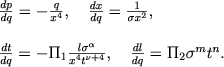
|
(5.15) |
Решение этой системы мы будем считать известным.
Очевидно, что система (5.14) описывает пульсации (есть вторая производная ![]() Но наличие производных по q означает, что имеет место своеобразная дисперсия. При исследовании пульсаций в плазме аналогичное явление называется пространственной дисперсией. Здесь эту особенность системы можно назвать дисперсией по лагранжевой координате.
Но наличие производных по q означает, что имеет место своеобразная дисперсия. При исследовании пульсаций в плазме аналогичное явление называется пространственной дисперсией. Здесь эту особенность системы можно назвать дисперсией по лагранжевой координате.
Применим теперь к системе (5.14) обычные методы теории малых колебаний. Воспользуемся приближением, эквивалентным методу Вентцеля - Крамерса - Бриллюэна, т. е. будем считать, что производные по q штрихованных величин много больше, чем производные по q не штрихованных величин.
Тогда решение системы (5.14) можно искать в виде
|
|
(5.16) |
где ω - безразмерная частота (выраженная в единицах времени т согласно (5.10)), а К - аналог волнового числа.
Подставляя (5.16) в (5.14), подучим систему:
![$$
\begin{array}{l}
-iKp' - \frac{\omega^2 x'}{xp} - \frac{q}{x^4p}(p' + 4x') = 0, \\ \\
-iKx^3\sigma x' + 3x' + \sigma' = 0, \\ \\
-iKx^4t^{\nu+4}t' + \Pi_1l\sigma^2[l' + \alpha\sigma' - (\nu + 4)t' - 4x'] = 0, \\ \\
-iKl' - \Pi_2 \frac{\sigma^mt^n}{l}(m\sigma' + nt' - t') + \Pi_5\frac{p}{\sigma l}i\omega\left(\sigma' - \frac{1}{\Gamma - 1}t'\right) = 0, \\ \\
p' - \frac{\sigma^\xi t^\eta}{p}(\xi\sigma' + \eta t') + 4\Pi_3\frac{t^4}{p}t' = 0.
\end{array}
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula68.gif)
|
(5.17) |
Это и есть система однородных уравнений (но с переменными коэффициентами). Исключая отсюда все штрихованные величины, можно получить дисперсионное соотношение, определяющее зависимость ω(К). В общем виде дисперсионное соотношение получается громоздким, поэтому не будем его выписывать. Существенно легче понять всю картину, если сначала максимальным образом упростить систему (5.17), а потом последовательно учитывать все более сложные случаи.
Наиболее простой случай - пульсации без дисперсии по лагранжевой координате, т. е. при К = 0. Этот случай называется моделью одной зоны (см. статью Беккера в [4]). В самом деле, здесь колебания каждого слоя в звезде происходят независимо от других слоев, хотя параметры пульсаций разных слоев различны. Упростим задачу еще дальше. Поскольку пульсации обычно имеют место в слоях звезды вблизи ее поверхности, пренебрежем ролью лучевого давления (Π3 = 0) и термоядерными реакциями (Π2 = 0). Тогда дисперсионное соотношение оказывается совсем простым, из него выпадает даже комплекс Π5.
Пульсации в этом случае имеют адиабатический характер (t' = (Γ - 1)σ') и частота этих пульсаций определяется кубическим уравнением
|
|
(5.18) |
где введены новые обозначения:
|
|
(5.19) |
Из уравнения (5.18) следует существование трех решений:
|
|
(5.20) |
Если от безразмерной частоты со перейти к размерным частотам и периодам, то получим следующее выражение для периода колебаний слоя на расстоянии с от центра звезды:
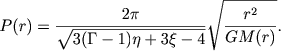
|
(5.21) |
При η = ξ = 1 численный множитель оказывается равным ![]() . Итак, пульсации слоя возможны, если B < 0 (эквивалентно условию Γ < 4/3 при η = ξ = 1) и период колебаний, как и следовало ожидать, обратно пропорционален корню из средней плотности части звезды, ограниченной пульсирующим слоем.
Это и есть самый простой случай. Будем теперь усложнять модель. Попытаемся сначала учесть возможную неадиабатичность колебаний. Иными словами, допустим, что между разными пульсирующими слоями происходит обмен энергией. Но, по-прежнему, будем пренебрегать лучевым давлением (Π3 = 0) и термоядерными реакциями (Π2 = 0).
. Итак, пульсации слоя возможны, если B < 0 (эквивалентно условию Γ < 4/3 при η = ξ = 1) и период колебаний, как и следовало ожидать, обратно пропорционален корню из средней плотности части звезды, ограниченной пульсирующим слоем.
Это и есть самый простой случай. Будем теперь усложнять модель. Попытаемся сначала учесть возможную неадиабатичность колебаний. Иными словами, допустим, что между разными пульсирующими слоями происходит обмен энергией. Но, по-прежнему, будем пренебрегать лучевым давлением (Π3 = 0) и термоядерными реакциями (Π2 = 0).
При неадиабатических пульсациях ![]() . Поэтому в четвертом уравнении следует сохранить член iKl'. Это и очевидно, поскольку теперь из-за обмена энергией появляется и дисперсия по лагранжевой координате. Если сохранить члены с iK во всех уравнениях системы (5.17), то дисперсионное уравнение опять окажется громоздким.
. Поэтому в четвертом уравнении следует сохранить член iKl'. Это и очевидно, поскольку теперь из-за обмена энергией появляется и дисперсия по лагранжевой координате. Если сохранить члены с iK во всех уравнениях системы (5.17), то дисперсионное уравнение опять окажется громоздким.
Но можно воспользоваться следующими рассуждениями. Допустим, что частота пульсаций каждого слоя звезды определяется только параметрами, соответствующими положению слоя внутри звезды, а взаимодействие между слоями сводится лишь к появлению неадиабатич-ности. Тогда в уравнениях (5.17) можно сохранить лишь член iKl', а все остальные члены с iK опустить. В этом случае дисперсионное уравнение опять оказывается сравнительно простым:
|
|
(5.22) |
где новые коэффициенты А и С суть:
|
|
(5.23) |
Уравнение (5.22) для случая η = ξ = 1 было получено из других соображений Беккером (см. [4]).
Сразу из (5.22) следует, что учет неадиабатичности приводит к появлению мнимых членов в частотах пульсаций, т. е. к затуханию или раскачке этих колебаний.
Уравнение (5.22) можно легко решить для случая, когда множитель ![]() мал. Воспользуемся этим приближением. Будем искать решение в виде
мал. Воспользуемся этим приближением. Будем искать решение в виде
|
|
(5.24) |
где s ≫ l. Если подставить (5.24) в (5.16), то получим
|
|
Отсюда следует, что в случае s > l пульсации затухают, причем s есть число колебаний перед тем, как их амплитуда уменьшится в 2,7 раза. Величина s называется добротностью. Если s < l, то колебания раскачиваются и система оказывается неустойчивой.
Подставим (5.24) в (5.22), сохранив только члены первого порядка по 1/s и считая, что 1/s и ![]() одного порядка малости. Тогда получим
одного порядка малости. Тогда получим
|
|
(5.25) |
Перейдем к размерным величинам, учитывая также определения (5.21) и (5.23). Получим
|
|
(5.26) |
где
|
|
(5.27) |
Безразмерное волновое число K согласно (5.16) есть характеристика массы слоя с заметным обменом энергией. Можно приближенно считать, что K ≈ M/ΔM, где ΔM - масса этого слоя. В таком случае Uk(r) есть, с точностью до численного множителя, величина тепловой энергии этого слоя. Произведение P(r)L(r) есть количество энергии, проходящей через этот слой за один период пульсации. Очевидно, что величина Uk(r)/P(r)L(r) много больше единицы. Заметим, что s с точностью до численного множителя соответствует обратной величине комплекса Π2 в (1.21). Знак величины s определяется знаком знаменателя, поскольку при пульсациях знак числителя всегда положителен. Пульсации затухают, если
|
|
(5.28) |
и раскачиваются в противоположном случае. Условие (5.28) называется условием колебательной устойчивости. Перепишем его в несколько другом виде:
|
|
Каждый из членов этого соотношения имеет определенный физический смысл. Первый член 4(Г - 1) определяет потерю механической энергии при сжатии и разрежении газа - эта потеря всегда приводит к затуханию колебаний. В зоне существенной ионизации величина Г-1 мала и поэтому потеря механической энергии невелика. Третий член 4/3 описывает эффект сферической геометрии. В плоском пульсирующем слое величину 4/3 следует опустить.
Основным является второй член, который учитывает изменение непрозрачности за период пульсации. Увеличение плотности и температуры при сжатии может и увеличить и уменьшить непрозрачность в зависимости от соотношения между α и ν . Если α - (Г - 1)ν < 0 (как это имеет место, например, в законе Крамерса при не слишком малых Г-1), то поглощение при сжатии преобладает над переизлучением при расширении и поэтому здесь тоже имеет место затухание пульсации. Однако в зонах ионизации Г-1 мало и, кроме того, показатель ν при низких температурах меняет знак, так что величина α - (Г - 1)ν < 0 может оказаться положительной и достаточно большой и вместо затухания колебаний появляется раскачка. Именно таким путем поддерживаются незатухающие пульсации, когда затухание колебания в одних слоях при выполнении условия (5.28) компенсируется "отрицательной диссипацией" в других слоях с обратным знаком неравенства (5.28). Как показал С. А. Жевакин еще в 1953 г., зона вторичной ионизации гелия служит источником поддержания пульсаций переменных звезд. Последующие расчеты (см. ниже) показали, что и в зонах ионизации водорода имеет место "отрицательная диссипация". К вопросу об условиях поддержания пульсаций мы вернемся ниже.
Третье решение уравнения (5.23), соответствующее решению ω = 0 в уравнении (5.18), можно искать сразу, полагая ω в (5.22) малой величиной (т. е. пренебрегая членами с ω2). Тогда получим
|
|
(5.29) |
Отсюда находим условие так называемой вековой, или секулярной, устойчивости звезды:
|
|
(5.30) |
Отсюда, кстати, следует, что в случае ξ < 1 и η < 1 звезда становится более устойчивой, чем при η = 1 и ξ = 1.
Вернемся к общей системе (5.17) и рассмотрим ее в другом приближении. Как уже отмечалось, неадиабатичность колебаний требует, чтобы t' ≠ (Γ - 1)σ'. Выше для учета неадиабатичности сохранялся член с iK. Его можно опустить, но зато сохранить члены с Π2. Поэтому рассмотрим систему (5.17) при следующих условиях. Положим К = 0, но сохраним члены с Π2, Π5 и Π3. Это означает, что теперь мы учитываем возможность выделения термоядерной энергии в пульсирующем слое, а также учитываем влияние лучевого давления. Но зато опять не учитывается взаимодействие между пульсирующими слоями (однослойная модель).
В такой постановке система (5.17) может описывать, например, пульсации в слоевых источниках горения водорода или гелия, которые рассматривались в предыдущей главе. Но применимость этого случая даже шире. Ведь формула ε = ε0ρmTn может описывать не только термоядерные реакции. Всегда, когда в веществе есть необратимое выделение или поглощение энергии по какому-либо закону, можно использовать эту формулу с соответствующим подбором коэффициентов е0, тип. В случае необратимого поглощения энергии ε0 < 0. Условие "необратимости" выделения или поглощения энергии означает, что рассматриваются механизмы, всегда действующие только в одном направлении.
Учет лучевого давления (сохранение параметра Π3) проведем, используя обозначение β - отношение газового давления к полному. Поскольку метод получения дисперсионного уравнения для этого случая ничем не отличается от рассмотренного ранее, то мы ограничимся лишь записью окончательных формул. Из третьего уравнения (5.17) видно, что дисперсионное соотношение при К=0 будет зависеть от отношения Π2/Π5, а не от каждого из этих комплексов по отдельности. Поэтому удобнее рассмотреть предельные случаи, когда величина
|
|
(5.31) |
много больше либо много меньше единицы.
Как и раньше, исключая из (5.17) все штрихованные величины, получим дисперсионное уравнение, из которого, если пренебречь членом либо пропорциональным Q, либо пропорциональным 1/Q (в зависимости от величины этого комплекса), следует три решения. Одно из них всегда соответствует нулевой частоте, а два других, различающихся только знаком (как и в случае (5.20)), соответствует колебаниям с периодами
![$$
P(r) = \frac{2\pi}{\sqrt{(\Gamma - 1)[\beta\eta + 4(1-\beta)] + 3\beta\xi - 4}}\sqrt{\frac{r^3}{GM(r)}},
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula88.gif)
|
(5.32) |
![$$
P(r) = \frac{2\pi}{\sqrt{\frac{3\alpha + 4 + 3m}{\nu + 4 - n}[\beta\eta + 4(1-\beta)] + 3\beta\xi - 4}}\sqrt{\frac{r^3}{GM(r)}},
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula89.gif)
|
(5.33) |
Из (5.33) также .следует, что пульсации возможны, если показатель не слишком большой, иначе подкоренное выражение или эффективный политропный индекс станут отрицательными.
Следующее приближение, т. е. сохранение членов с Q или 1/Q, позволит определить условие раскачки или затухание пульсации. Не будем приводить здесь формулы, аналогичные (5.26), но выпишем сразу критерий затухания пульсации:
|
|
(5.34) |
Эта формула справедлива как при Q ≪ 1, так и при Q ≫ 1. Неравенство (5.34) переходит в (5.28) при n = m = 0, как это и следовало ожидать. Также очевидно, что учет необратимого выделения энергии всегда облегчает раскачку пульсаций - в критерий (5.34) оба показателя n и m входят со знаком минус. Любопытно, что критерий раскачки не зависит от роли лучевого давления.
Критерий вековой, или секулярной, устойчивости в случае Q ≪ 1 имеет вид
|
|
(5.35) |
Это условие обобщает (5.30) на случай учета необратимого выделения энергии и лучевого давления.
Рассмотрение разных моделей пульсаций можно было бы продолжить, но мы вернемся к первому простому случаю, ибо именно этот случай описывает, конечно в грубом приближении, реальные пульсации переменных звезд, где всегда пульсируют слои, расположенные вблизи поверхности.
Формула (5.21) определяет период пульсаций некоторого слоя, а формула (5.26) характеризует раскачку или затухание колебаний в этом слое (определенном заданной величиной К) - Согласно методу получения решения было принято, что в пульсирующем слое все параметры (т. е. невозмущенные плотность, температура, коэффициенты α, ν, η, m и т. п.) постоянны либо меняются медленно.
В реальной пульсирующей звезде положение, конечно, существенно сложнее. Во-первых, пульсирует не один слой, в котором параметры не меняются по толщине, а довольно широкая зона, на протяжении которой и невозмущенные параметры и меняющиеся со временем величины варьируются на порядки. Более того, и это основное для объяснения пульсаций, в одной части всей этой зоны имеет место положительная диссипация энергии (выполнено неравенство (5.28)), которая должна обязательно компенсироваться отрицательной диссипацией в другой части зоны, иначе пульсации будут быстро затухать. Иными словами, в пульсирующих звездах параметр s должен менять знак на протяжении всей пульсирующей зоны. Учет этого эффекта можно провести, разбив всю зону на отдельные слои, в пределах которых можно считать постоянными отдельные параметры, и решать систему связанных уравнений, описывающих колебания всех слоев.
Во-вторых, в реальной пульсирующей звезде существенны и нелинейные эффекты. Сжатие и разрежение газа при пульсациях изменяют как условия переноса излучения (поскольку, как мы видели, коэффициент непрозрачности очень чувствителен к вариациям температуры), так и степень ионизации: в зонах, где происходит ионизация водорода и гелия, даже небольшие изменения температуры приводят к существенному изменению состояния ионизации. Это означает, что даже при относительно небольших пульсациях неравенства (5.28), которые могут быть выполнены, например, в момент наибольшего сжатия, могут превратиться в обратные неравенства в момент наибольшего расширения, или наоборот. Иными словами, раскачка пульсаций основана на таком тонком балансе всех величин, что при не очень больших амплитудах параметр s начинает менять знак уже в течение одного периода. Следовательно, при больших амплитудах раскачка пульсаций прекращается.
Возможны и другие нелинейные эффекты - образование ударных волн, взаимодействие радиальных и нерадиальных пульсаций и т. д.
В-третьих, степенное представление коэффициента непрозрачности в виде ϰ = ϰ0ρα/Tν является очень грубым приближением, особенно в области ионизационных зон, где коэффициент непрозрачности велик и меняется с температурой очень существенно. Поэтому для анализа пульсаций реальных звезд приходится пользоваться таблицами коэффициента непрозрачности.
В-четвертых, в зонах ионизации большую роль играет конвективный перенос энергии. Раскачка колебаний связана с реакцией коэффициента непрозрачности на изменения температуры и плотности при пульсациях и поэтому при замене лучистого переноса энергии на конвективный перенос весь эффект вообще исчезает.
Все сказанное выше означает, что более или менее адекватный анализ явления пульсаций звезд можно провести лишь в рамках численного моделирования всего явления путем численного же решения основной системы уравнений (5.1), (5.3), (5.4), (5.8) с использованием табличных данных для коэффициента непрозрачности ϰ. Здесь трудно найти условия подобия моделей пульсирующих звезд, поскольку приходится рассчитывать отдельную модель для каждой звезды с конкретно заданными параметрами (масса, светимость, поверхностная температура).
Такие расчеты для различных звезд проводились неоднократно. С методикой расчета можно познакомиться по статьям Кокса и Кристи в [4, 5] и по работе В.И.Алешина [6]. Метод расчета заключается в следующем. Сначала рассчитывается модель стационарной равновесной звезды. Затем ей задается некоторое возмущение и прослеживаются пульсации звезды на много колебаний до тех пор, пока устанавливается определенный период и амплитуда пульсации. При решении приходится разбивать зоны ионизации на большое число слоев.
Поскольку внутренняя часть звезды, в частности, область, где протекают термоядерные реакции, почти не участвует в пульсации (здесь нет раскачки, т. е. неравенства (5.28) всегда выполнены), то можно считать, что на внутренней границе пульсирующей зоны все параметры и, в частности, поток энергии Lr, остаются все время постоянными. Оценки показывают, что амплитуда колебаний здесь менее 10-3 от амплитуды пульсаций на поверхности [5]. На внешней границе давление и плотность обращаются в нуль, но при этом температура газа приравнивается к эффективной температуре звезды.
Результаты расчетов можно представить в виде таблиц и графиков, иллюстрирующих изменение разных параметров как на поверхности звезды, так и в глубоких слоях. В качестве примера приведем некоторые результаты расчета Кристи [7, 8].
Выбрана модель звезды с параметрами М=0,4M☉, L = 1,5 ⋅ 1035 эрг ⋅ сек-1, Тeff = 6500°; К. Внешние слои звезды разбивались на сорок слоев (нумерация из глубины к поверхности) и прослеживалось движение каждого слоя. Было задано некоторое начальное синусоидальное возмущение в глубине и просчитывалась дальнейшая эволюция системы. Стационарное значение периода, равное 5,7 ⋅ 104 сек, устанавливается очень быстро, всего через несколько колебаний. Начальная амплитуда изменения радиуса звезды была принята равной 10%. Стационарное значение амплитуды оказалось равным 18%. Амплитуда колебаний светимости возросла с 8% до 13% и тоже установилась на этом уровне.
На рис. 17 показано изменение скорости движения слоев со временем и на разных глубинах. В более глубоких слоях движения синусоидальны, ближе к поверхности амплитуда колебаний растет, появляются вторичные максимумы. На рис. 18 показано изменение светимости на разных глубинах. Здесь амплитуда максимальна в зонах ионизации, а ближе к поверхности изменение светимости в течение периода опять уменьшается. Кривая светимости заметно несинусоидальна, с более крутым подъемом и пологим уменьшением яркости.
На рис. 19 даны диаграммы р - V(V = 1/р - удельный объем) для разных зон. Площадь внутри петли определяет работу, выполненную газом при сжатии и разрежении в течение одного периода. Диссипация энергии соответствует движению вдоль цикла против часовой стрелки, раскачка пульсации - движению по часовой стрелке (движение вдоль цикла указано стрелками). На рис. 19 видно, что слой 22 имеет положительную диссипацию, но здесь пульсации почти адиабатичны (площадь петли мала). Этот слой находится под зоной ионизации гелия. В слое 24 у основания зоны часть цикла имеет
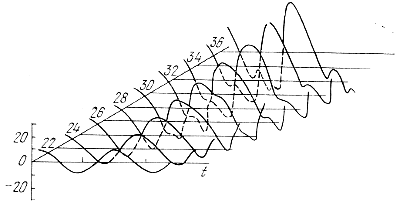
Рис. 17. График изменения скорости движения слоев на разных глубинах в течение одного периода.
Числа - номера слоев (счет от более глубоких слоев к поверхности). Амплитуда максимальна вблизи поверхности.
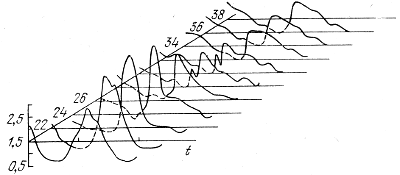
Рис. 18. Изменение светимости на разных глубинах в течение одного
периода.
Амплитуда изменений светимости максимальна на некоторой глубине.
положительную диссипацию, часть - отрицательную (это следует из перехлеста петли). В зонах ионизации гелия (слои 26 - 28) имеет место раскачка колебаний отрицательная диссипация). В зоне ионизации водорода (слой 32) также происходит раскачка колебаний.
Подсчет общей площади циклов с раскачкой пульсаций показывает, что 2/3 отрицательной диссипации генерируется в зоне ионизации гелия, а одна треть - в зоне ионизации водорода. Обе зоны за один период пульсации забирают из потока лучистой энергии, проходящей через эти слои, 11 % энергии. Из этого количества 78% уходит на погашение потерь энергии при колебаниях с положительной диссипацией более глубоких слоев (в самых верхних слоях диссипация тоже положительна, но она мала), а 22% превращается в кинетическую энергию. Таким образом, коэффициент полезного действия пульсирующей звезды как тепловой машины равен 2,4% т. е. достаточно мал.
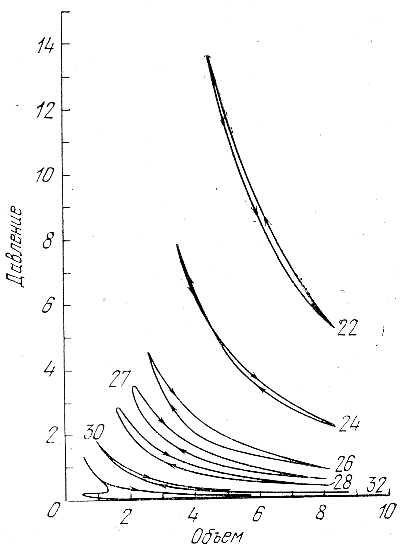
Рис. 19. Диаграмма давление - объем для некоторых слоев в пульсирующей звезде.
Площадь петли соответствует работе за период. Диссипация энергии - обход против часовой стрелки, раскачка колебаний - обход по часовой стрелке. Шкала ординат - давление в единицах 10-3 дин/см3, шкала абсцисс - объем слоя с соответствующим номером в единицах 1033 г/ρ , где ρ - плотность в этом слое.
Хотя пока рассчитано еще немного моделей пульсаций звезд, можно сделать некоторые качественные и даже количественные выводы о месте этих звезд в общем характере звездной эволюции. Пульсирующие звезды принадлежат к ветви красных гигантов и занимают на диаграмме Рессела - Герцшпрунга довольно узкую полосу. По мере развития красного гиганта из горячей звезды главной последовательности ее поверхность раздувается и поверхностная температура падает. У горячих звезд водород и гелий ионизованы вплоть до самой поверхности. При падении поверхностной температуры образуются ионизационные зоны, которые при дальнейшем понижении Тeff оказываются под ее поверхностью. В этот момент создаются условия, благоприятные для возбуждения и поддержания пульсаций. Таким образом, пульсировать звезда начинает тогда, когда ее эволюционный трек пересекает область на диаграмме Рессела - Герцшпрунга, в которой зоны ионизации находятся недалеко под поверхностью. При этом ускорение силы тяжести здесь должно быть относительно невелико.
Однако все численные расчеты проводились для отдельных конкретных моделей звезд. Возникает вопрос, можно ли получить какие-либо критерии подобия, общие соотношения для параметров пульсирующих звезд? Очевидно, что первым критерием подобия служит соотношение (5.21), связывающее период со средней плотностью. Можно было бы также ожидать, что критерием подобия является и определение (5.26) - пульсирующие звезды подобны, если s у этих звезд одинаково. Величина s зависит от двух характеристик, которые легко определить, - периода P и светимости L, и одной характеристики, которую труднее оценить, - тепловой энергии пульсирующего слоя Uk. В первой главе был получен безразмерный комплекс (формула (1.21)), куда входила полная энергия звезды; там было показано, что этот комплекс сильно меняется у разных звезд и поэтому не может быть критерием подобия. Вероятно, и величину s из (5.26) нельзя рассматривать как критерий подобия. По-видимому, это связано с тем, что в пределах всей пульсирующей зоны параметр s из (5.26) меняет знак и вообще варьируется в широких пределах.
Впрочем, в ряде работ (см. [3, 7]) предлагался критерий подобия вида
|
|
(5.36) |
следующий из условия s = const, если предположить, что относительная масса пульсирующего слоя более или менее одинакова у всех пульсирующих звезд. Температура в зонах ионизации тоже одинакова и поэтому Uk ∼ ΔM ∼ M.
Но в настоящее время условия подобия пульсирующих звезд обычно получают путем обобщения результатов численных расчетов. Например, Ибен [9] дает следующую формулу, позволяющую определить период пульсаций звезд типа RR Лиры:
|
|
(5.37) |
где Тeff - поверхностная температура этих звезд. В этом соотношении можно перейти от Тeff к радиусу звезды, так как L = 4πσТ4effR2, и ввести среднюю плотность. Тогда получим
|
|
(5.38) |
в то время как из элементарной теории подобия следует ![]() . Итак, хотя некоторая зависимость критерия подобия от массы и светимости звезды есть, но отклонения сравнительно невелики.
. Итак, хотя некоторая зависимость критерия подобия от массы и светимости звезды есть, но отклонения сравнительно невелики.
Второй критерий подобия, определяющий условия раскачки и затухания пульсаций, т. е. параметр s, должен, вообще говоря, связать массу и светимость звезд с химическим составом зон ионизации, ибо именно этот состав и определяет поведение коэффициента поглощения. Ибен [9] предлагает следующие формулы:
|
|
|
|
где Y и Z - концентрации гелия и тяжелых элементов соответственно. Правда, Ибен подчеркивает, что эти формулы могут быть использованы лишь для очень грубых оценок параметров пульсирующих звезд типа RR Лиры.
Вообще нужно иметь в виду, что сложная структура реальных пульсирующих звезд вряд ли способствует нахождению простых критериев подобия для этих объектов.
<< § 4.5 Численное моделирование эволюции звезд | Оглавление | § 5.2 Вращение и магнитные поля звезд >>