Астронет > Размерности и подобие астрофизических величин

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Размерности и подобие астрофизических величин << § 4.3 Белые карлики и нейтронные звезды | Оглавление | § 4.5 Численное моделирование эволюции звезд >>

§ 4.4 Звезды с лучистым переносом энергии

Лучистый перенос энергии определяет основные свойства и структуру большинства звезд. Правда, вероятно, вообще нет звезд, в которых по всей их массе энергия переносилась бы только излучением. В реальных условиях есть слои и с лучистым и с конвективным переносом. В отличие от конвекции, поток энергии, переносимый лучистой теплопроводностью, лимитируется величиной коэффициента непрозрачности. Поэтому звезда как бы приспосабливается к условиям переноса энергии излучением, и ее структура определяется в первую очередь потоком лучистой энергии в тех слоях, где нет конвекции.

Задача заключается в том, чтобы, используя эту особенность строения звезд, найти критерии подобия и определить связи между основными параметрами звезды. Разумеется, мы не будем рассматривать в деталях теорию внутреннего строения звезд. В соответствии с основной темой книги основное внимание уделяется критериям подобия.

Вообще говоря, начало развития теории внутреннего строения звезд тоже было связано с принципом подобия. Еще в 1921 г. Эддингтон предположил, что все звезды построены по одной, названной им стандартной, модели, описываемой политропой с индексом n=3. Считалось, что параметр β из (4.12) одинаков по всей звезде, т.е. р ∼ T⁴ ∼ ρ^4/3, а коэффициент непрозрачности и мощность источников энергии подбирались так, чтобы удовлетворить этому условию. Итак, по стандартной модели все звезды подобны, а различие их масс и светимостей определяется различием в значении параметра β - отношения лучевого давления к полному. Радиус звезды в этой модели теоретически не определен, поскольку, как известно, в политропе с n = 3 радиус не зависит от массы. Из формулы (4.12) при заданном β можно найти величину K_4/3 для соотношения р = K_4/3ρ^4/3, а следовательно, по (4.36), и массу звезды с данным β Окончательный результат таков (см., например, [5]):

$M = \frac{8}{G^{3/2}}\left(\frac{\Re}{\mu}\right)^2\left[\frac{1-\beta}{a\beta}\right]^{1/2} = \frac{9,6}{\mu^2}\frac{(1-\beta)^{1/2}}{\beta^2}M_\odot.$ (4.54)

Случай β = ½ , где М ≈ 50М_☉/μ², был рассмотрен в гл. 3, где эта величина принималась близкой к верхнему пределу масс. У звезд малой массы β близко к единице.

На основе этой стандартной модели Эддингтоном было обнаружено и исследовано соотношение масса - светимость, а Стремгреном было дано объяснение главной последовательности на диаграмме Рессела - Герцшпрунга. Использование стандартной модели было оправдано тем, что в то время не было никаких данных об источниках энергии в звездах. До создания теории термоядерных источников энергии были предложены и другие модели звезд, также основанные на принципе подобия. В частности, следует отметить модель Коулинга, учитывающую в явном виде закон поглощения Крамерса и предполагающую, что источники энергии расположены в центре звезды. В этой модели имеется конвективное ядро в центре с радиусом 16,9% и с массой 14,5% от радиуса и массы звезды. Как мы увидим ниже, эта модель с конвективным ядром оказалась довольно близкой к реальным моделям с термоядерными источниками энергии.

Более полный анализ подобия звездных моделей, основанный на применении принципа подобия, появился уже после создания теории термоядерных источников энергии. Одним из первых было исследование Л. И. Седова ([16, 17]). Изложение подобного анализа дано также в книгах [1, 4]. Расчет структуры подобных моделей звезд дан В. С. Имшенником и Д. К. Надежиным [18]. Следующее ниже изложение основано на этих работах.

Запишем еще раз полную систему уравнений внутреннего строения звезды с учетом всех известных нам условии, предполагая лучистый перенос энергии:

$\left. \begin{array}{l} \frac{dp}{dr} = -\frac{GM(r)}{r^2}\rho, \quad \frac{dM}{dr} = 4\pi r^2\rho, \\ \\ \frac{d}{dr}\left[\frac{1}{3} aT^4\right] = -\frac{\varkappa L(r)}{4\pi r^2c}\rho, \, \frac{dL}{dr} = 4\pi r^2\rho\epsilon, \\ \\ p = \frac{\Re}{\mu}\rho T + \frac{1}{3}aT^4, \quad \mu = \mu(X, Y, Z),\\ \\ \varkappa = \varkappa_0\frac{\rho^{\alpha}}{T^\nu}, \quad \epsilon = \epsilon_0\rho^mT^n. \end{array} \right\}$ (4.55)

Если заданы величины μ, ϰ₀ и ε₀, а также основные параметры звезды М, L и R, то эта система может быть решена полностью при следующих граничных условиях:

$\begin{array}{l} r = 0, \, M = 0, \, p, \, \rho - \mbox{конечны},\\ r = R, \, p = \rho = 0. \end{array}$ (4.56)

Система (4.55) - (4.56) справедлива, если ни в ядре звезды, ни вблизи ее поверхности нет зон, в которых энергия переносится конвекцией. Этот случай и рассматривался Л. И. Седовым ([17, 18]). Приведем здесь соотношения, полученные им из соображений размерности и принципа подобия (но в других обозначениях).

В звезде с лучистым переносом энергии нет перемешивания вещества и поэтому можно ожидать, что химический состав вещества меняется вдоль радиуса. В выражениях для ε и ϰ это можно учесть некоторым изменением показателей α , ν , m и n, считая величины ϰ₀ и ε₀ постоянными, а в выражении для молекулярного веса можно предположить существование зависимости

$\mu = \mu_0\rho^{1-\xi}T^{1-\eta},$ (4.57)

где ξ и η - некоторые постоянные числа. Введем теперь новые безразмерные переменные при помощи преобразования, обобщающего (4.33):

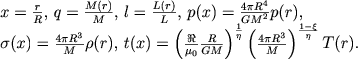
$\begin{array}{l} x = \frac{r}{R}, \, q = \frac{M(r)}{M}, \, l=\frac{L(r)}{L}, \, p(x) = \frac{4\pi R^4}{GM^2}p(r),\\ \sigma(x) = \frac{4\pi R^3}{M}\rho(r), \, t(x) = \left(\frac{\Re}{\mu_0}\frac{R}{GM}\right)^{\frac{1}{\eta}}\left(\frac{4\pi R^3}{M}\right)^{\frac{1-\xi}{\eta}}T(r). \end{array}$ (4.58)

Более сложное преобразование для температуры определяется необходимостью учета соотношения (4.57). В других работах обычно пренебрегается изменением молекулярного веса, и тогда можно считать ξ = η = 1. Формула для перехода от Т(r) к t(x) оказывается более простой.

Теперь запишем уравнения (4.55) в безразмерном виде:

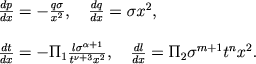
$\begin{array}{l} \frac{dp}{dx} = -\frac{q\sigma}{x^2}, \quad \frac{dq}{dx} = \sigma x^2,\\ \\ \frac{dt}{dx} = -\Pi_1\frac{l\sigma^{\alpha + 1}}{t^{\nu + 3}x^2},\quad \frac{dl}{dx} = \Pi_2\sigma^{m+1}t^n x^2. \end{array}$ (4.59)

Здесь появились два безразмерных комплекса:

$\Pi_1 = \frac{3\varkappa_0 L}{16\pi caR^2}\left(\frac{M}{4\pi R^3}\right)^{\alpha + 1 -\frac{\nu+3}{\eta}(1-\xi)} \left(\frac{\Re}{\mu_0}\frac{R}{GM}\right)^{\frac{\nu+3}{\eta}},$ (4.60)

$\Pi_2 = \frac{4\pi\epsilon_0 M}{L}\left(\frac{M}{4\pi R^3}\right)^{m + 1 + \frac{n}{\eta}(1-\xi)} \left(\frac{\mu_0}{\Re}\frac{GM}{R}\right)^{\frac{n}{\eta}},$ (4.61)

и выражение для полного давления, записанное в безразмерном виде:

$p = \sigma^{\xi}t^{\eta} + \Pi_3t^4,$ (4.62)

где еще один безразмерный комплекс:

$\Pi_3 = \frac{a}{3}\left(\frac{\mu}{\Re}\frac{GM}{R}\right)^{\frac{4}{\eta}} \left(\frac{M}{4\pi R^3}\right)^{4\frac{1-\xi}{\eta}}\frac{4\pi R^4}{GM^2}.$ (4.63)

В частном случае постоянного молекулярного веса (ξ = η = 1) безразмерный комплекс Π₃ зависит только от массы звезды:

$\Pi_3 = \frac{4\pi a}{3}\left(\frac{\mu_0}{\Re}\right)^4 G^3M^2 = \frac{4\pi^3}{45}\frac{\mu^4M^2}{m_p^2}\delta^2 = 0,78\mu_0^4\left(\frac{M}{M_\odot}\right)^2,$ (4.64)

где, по-прежнему, δ = Gm_p²/ħc. Очевидно, что Π₃ характеризует относительную роль лучевого давления.

Наконец, безразмерные граничные условия будут иметь такой вид:

$\begin{array}{l} x = 0, \, q = 0, \, l = 0, \, p, \, \sigma, \, t - \mbox{конечны},\\ x = 1, \, q = l = 1, \, p = \sigma = 0. \end{array}$ (4.65)

Таким образом, задача свелась к решению безразмерных уравнений (4.59) и (4.62) с граничными условиями (4.65). Решение характеризуется тремя безразмерными комплексами: Π₁, Π₂, Π₃. Очевидно, что эти комплексы могли быть получены и из простых соображений размерности путем построения матрицы размерности для размерных определяющих параметров М, L, R, G, а, μ₀m_p/k, ϰ₀ и ε₀, характеризующих звезду с лучистым переносом энергии и лучевым давлением.

Один из трех комплексов, например, Π₃, должен задаваться произведением [х0М. Численные значения комплексов Π₁ и Π₂ тогда будут получены при решении системы (4.59) как ее собственные значения. В результате можно найти соотношения Π₁ = ƒ(Π₃) и Π₂ = ƒ(Π₃), а следовательно, и две зависимости, например, светимости звезды и радиуса звезды от ее массы при заданных значениях размерных и безразмерных (показатели степени) определяющих параметров.

В случае, когда роль лучевого давления мала, т. е. относительно мала масса звезды, можно пренебречь лучевым давлением, и тогда безразмерные комплексы Π₁ и Π₂ оказываются не зависящими от Π₃. Правда, без решения системы (4.59) нам не удастся определить их численное значение, но можно утверждать, что оба эти комплекса являются константами. Отсюда и следуют две зависимости светимости и радиуса звезды от значения ее массы, впервые полученные Л. И. Седовым. Удобнее записать эти соотношения в логарифмическом виде (см. [17]):

$\lg R = \frac{(2+\alpha+m)\eta-(4+\nu-n)(2-\xi)}{(4+3\alpha+3m)\eta+(4+\nu-n)(3\xi - 4)} \lg M + const,$ (4.66)

$\lg L = \left[1+m+\frac{2-\xi}{\eta}n+\frac{[(2+\alpha + m)\eta - (4+\nu - n)(2-\xi)][(3\xi - 4)n - 3m\eta]}{\eta[(4+3\alpha + 3m)\eta + (4+\nu -n)(3\xi-4)]}\right]\lg M + const.$ (4.67)

Численные значения безразмерных комплексов Π₁ и Π₂ в работах [16, 17] не определялись, поэтому величины констант в (4.66) и (4.67) остались неизвестными.

Задаваясь определенным выбором параметров α и ν , n и m, ξ и η, можно получить степенные зависимости L и R как функции от М. В простейшем случае α = 1, ν = 7/2 (закон Крамерса), m = 1, n = 4 (протонный цикл) и ξ = η = 1 имеем

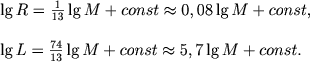
$\begin{array}{l} \lg R = \frac{1}{13}\lg M + const \approx 0,08 \lg M +const, \\ \\ \lg L = \frac{74}{13}\lg M + const \approx 5,7 \lg M +const. \end{array}$ (4.68)

To же самое, но для углеродного цикла (n=16) дает

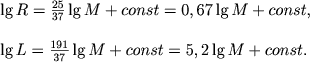
$\begin{array}{l} \lg R = \frac{25}{37}\lg M + const = 0,67 \lg M +const, \\ \\ \lg L = \frac{191}{37}\lg M + const = 5,2 \lg M +const. \end{array}$ (4.69)

Любопытно, что соотношение светимость - масса очень слабо зависит от характеристик термоядерных реакций. Как уже подчеркивалось, это связано с тем, что структура и свойства звезды в первую очередь определяются законом переноси энергии. Но радиус звезды существенно зависит от выбора закона выделения энергии. Для иллюстрации рассмотрим и случай, когда непрозрачность определяется рассеянием на электронах (соотношение (4.21), т. е. α = ν = 0). Пренебрегая опять изменением молекулярного веса, получим для водородного цикла (n=4):

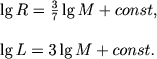
$\begin{array}{l} \lg R = \frac{3}{7}\lg M + const, \\ \\ \lg L = 3\lg M + const. \end{array}$ (4.70)

и для углеродного цикла (n=16):

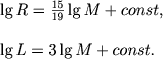
$\begin{array}{l} \lg R = \frac{15}{19}\lg M + const, \\ \\ \lg L = 3\lg M + const. \end{array}$ (4.71)

Здесь источники энергии вообще не влияют на соотношение масса - светимость. Заметим, что в этом случае мы вернулись к соотношению масса - светимость L ∼ M³, полученному из простых соображений размерности в гл. 3 (формулы (3.8) и (3.11)), также в предположении независимости коэффициента непрозрачности от плотности и температуры.

Сравнение с наблюдениями мы проведем в следующем параграфе, где рассмотрим результаты численного расчета. Кроме того, надо подчеркнуть, что в соотношениях (4.66) - (4.71) не учтено влияние лучевого давления.

Полное решение системы (4.59) - (4.65) для случая однородного молекулярного веса (ξ = η = 1), но с учетом лучевого давления и конвективного переноса, было дано В. С. Имшенником и Д. К. Надежиным [18]. Это решение позволило определить значения безразмерных комплексов Π₁ и Π₂ для разных выборов Π₃. Иными словами, в соотношениях (4.66) и (4.67) были получены значения констант и, более того, была определена зависимость этих констант от лучевого давления. Это означает, что, вообще говоря, соотношение светимость - масса определяется не только множителем перед lg М, в (4.67), но и зависимостью константы от массы, появляющейся из-за зависимости Π₂ от Π₃.

При расчетах численных значений безразмерных комплексов важно учесть и возможность образования конвективных ядер в центральных областях звезд. Это делается следующим образом. Третье уравнение (4.59), определяющее температурный градиент dt/dx справедливо только до тех пор, пока величина этого градиента остается меньше, чем адиабатический градиент температуры, найденный из (4.13). Как только градиент становится большим, наступает конвекция и третье уравнение (4.59) становится неприменимым. Вместо этого уравнения теперь следует из (4.13) и (4.1) определить градиент температуры в недрах звезды при переносе энергий адиабатической конвекцией. Имеем

$\frac{dT}{dr} = \frac{\partial T}{\partial p}\frac{\partial p}{\partial r} = -\frac{\gamma - 1}{\gamma}\frac{GM\rho T}{pr^2}.$ (4.72)

В безразмерных переменных (4.58)

$\frac{dt}{dx} = -\frac{2(4 - 3\beta)}{32 - 24\beta - 3\beta^2}\frac{q\sigma t}{px^2},$ (4.73)

где величина β (с сохранением переменности молекулярного веса)

$\beta = \frac{\sigma^\xi t^{\eta}}{\sigma^\xi t^{\eta} + \Pi_3 t^4} = \frac{1}{1+\Pi_3 t^{4-\eta}\sigma^{-\xi}}.$ (4.74)

Очевидно, что учет конвективных зон не изменит характера самой задачи нахождения собственных значений Π₁ и Π₂ при заданном Π₃. От наличия конвективных зон зависит только величина численных значений комплексов. Поэтому соотношения (4.66) - (4.71) с неопределенными значениями постоянных справедливы как для моделей без конвективных ядер, так и для моделей с конвективными ядрами.

Итак, основная задача заключается в нахождении собственных значений системы уравнений (4.59), где в области конвективного ядра третье уравнение (для dt/dx) заменяется на уравнения (4.73) - (4.74). Граничные условия даются соотношением (4.65).

Разумеется, аналитического решения этой задачи нет, можно получить лишь численные решения. Известной трудностью является большое количество разных параметров: α, ν , n, m, ξ и η и поэтому велико число разных вариантов решения.

В работе В. С. Имшенника и Д. К. Надежина [18] было рассмотрено несколько вариантов моделей с постоянным по всей звезде молекулярным весом, т. е. было принято условие ξ = η = 1.

В табл. 3 приведены характеристики некоторых из рассчитанных в [18] моделей. Задавалось значение комплекса Π₃, который согласно (4.64) зависит только от комбинации μ₀M². Решение системы на собственные значения дает тогда величины Π₁ и Π₂. Кроме того, в таблице приведены относительные значения радиуса (х_k) и массы (q_k) конвективного ядра.

Таблица 3

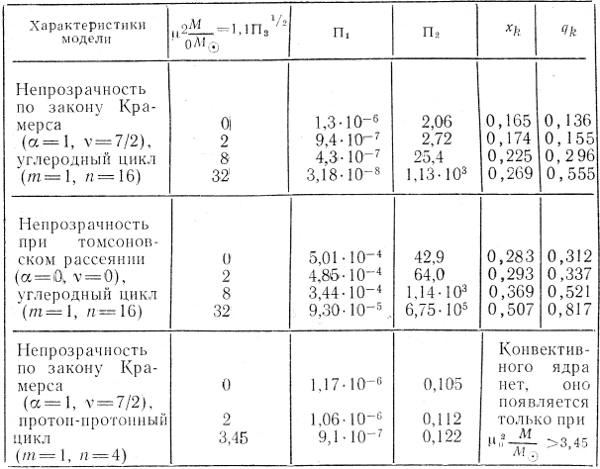
Из этой таблицы сразу следует, что комплекс Π₁ учитывающий роль коэффициента непрозрачности, относительно слабо зависит от выбора Π₃, хотя и более существенно зависит от выбора закона непрозрачности. Комплекс Π₂ очень сильно меняется с изменением роли лучевого давления. Также заметно меняются размеры и масса конвективного ядра.

В работе [18] было рассмотрено еще несколько моделей. Например, рассматривались звезды с углеродной реакцией при высоких температурах, когда n = 13, и звезды с гелиевой реакцией, где m=2, n ≈ 30. Здесь перенос энергии связан с рассеянием на свободных электронах, т.е. α = 0, ν = 0. Оказалось, что характеристики таких моделей мало отличаются от аналогичной модели в табл. 3. В частности, комплексы Π₁ остаются почти такими же по своему численному значению. Мало изменяются и параметры конвективного ядра. Только комплекс Π₂ оказался существенно отличным. Для моделей с μ₀²M/M_☉ = 32 он равен 3,45 ⋅ 10⁴ в случае горячей звезды с углеродным циклом и 1,09 ⋅ 10⁷ - в случае модели с гелиевой реакцией.

Анализ решений уравнений этой задачи при ξ ≠ 1 был проведен В. И. Петрухиной. Оказалось, что и здесь безразмерный комплекс Π₁ почти не меняется в интервале изменения ξ от 0,6 до 1,5. Даже комплекс Π₂ в этой задаче меняется всего на несколько процентов. Параметры конвективного ядра также почти не чувствуют изменения молекулярного веса.

Итак, резюмируя данные анализа уравнения строения звезд с точки зрения принципа подобия, можно утверждать следующее. В широком интервале возможных значений шести показателей α, ν , n, m, ξ и η величина безразмерного комплекса Π₁ может считаться почти постоянной. Все звезды подобны по безразмерному критерию (4.60).

С точки зрения физики звезд этот результат еще раз подчеркивает универсальность соотношения масса - светимость, основанного на безразмерном комплексе Π₁

Правда, учет лучевого давления (т. е. комплекса Π₃) все же приводит к заметным изменениям комплекса Π₁ Учитывая эти изменения, В. С. Имшенник и Д. К Надежин находят, что в области больших масс при непрозрачности из-за томсоновского рассеяния вместо (4.71) лучше подходит соотношение

$\lg L = 2,5\lg M + const.$ (4.75)

Формула (4.67) (в которой для того, чтобы убрать постоянную, лучше выразить светимость и массу в единицах светимости и массы Солнца) хорошо описывает соотношение масса - светимость при всех возможных вариантах, параметров, но при не слишком больших массах.

Разумеется, все сказанное относится только к теоретическому выводу критерия подобия, а отнюдь не к результатам сравнения теории и наблюдений. Наконец, нужно отметить и то, что хотя при учете лучевого давления для каждой конкретной массы звезды есть своя модель - и в этом смысле звезды разных масс не подобны друг другу,- все же строение их приблизительно одинаково и поэтому существует ограниченное подобие строения звезд разных масс с конвективными ядрами в центрах.

При построении рассмотренных выше моделей не учитывалась возможность образования конвективных зон вблизи поверхности звезды. Поэтому такие модели применимы только для звезд ранних спектральных классов, где водород и гелий ионизованы до самой поверхности и где поэтому не возникают поверхностные зоны ионизации. У звезд поздних спектральных классов поверхностная температура низка, в околоповерхностных слоях водород, а тем более гелий не ионизованы, что приводит к резкому увеличению непрозрачности. Кроме того, в зонах ионизации водорода и гелия существенно уменьшается и показатель адиабаты. Все это приводит к возбуждению конвекции, и в приповерхностных слоях звезд поздних спектральных классов энергия переносится конвекцией. Зато здесь не образуется конвективных ядер. Поскольку спектральный класс звезды связан с ее массой, то отсюда следует, что у звезд малых масс есть конвективная поверхностная зона (которая может дойти и до центра у звезд очень малых масс), а у звезд больших масс есть конвективное ядро (рис. 3).

Строго говоря, образование конвективной зоны вблизи поверхности должно следовать из решения основной системы уравнений, если в ней учесть все изменения коэффициентов непрозрачности и показателей адиабаты. Но это сделать трудно и поэтому лучше учесть образование поверхностных конвективных зон в граничных условиях.

Как известно, в конвективной зоне имеет место политропный закон р = К_γρ^γ Показатель γ вблизи поверхностных слоев заметно отличен от 5/3 (например, в конвективной зоне Солнца вблизи фотосферы γ ≈ 1,16). Но по мере погружения в глубь конвективной зоны величина γ быстро приближается к значению 5/3. Поэтому можно считать, что уже на некоторой небольшой глубине (где, скажем, q ≈ 0,95-0,98) плотность, температура ь давление вещества связаны условиями

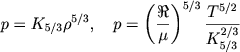
$p = K_{5/3}\rho^{5/3}, \quad p = \left(\frac{\Re}{\mu}\right)^{5/3}\frac{T^{5/2}}{K_{5/3}^{2/3}}$ (4.76)

Здесь параметр К_5/3 должен быть определен из теории звездных атмосфер, учитывающей неадиабатическую конвекцию. К сожалению, пока надежных определений параметра К_5/3 Для этого случая нет. Можно лишь получить грубые оценки.

Формула (4.76) в безразмерных переменных (4.58) имеет вид

$p = \Pi_4 t^{\frac{5\eta}{5-3\xi}}$ (4.77)

где новый безразмерный комплекс

$\Pi_4 = \left[4\pi\left(\frac{GM^{1/3}R}{K_{5/3}}\right)^{3/2}\right]^{\frac{2\xi}{5-3\xi}}.$ (4.78)

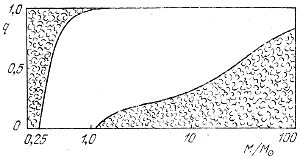
Рис. 3. Область конвективных зон и конвективных ядер у звезд разных масс.

Мы не учли возможную зависимость параметра К_5/3 от молекулярного веса, который в преобразовании (4.58) считается меняющимся. Впрочем, до сих пор при рассмотрении моделей звезд и поверхностными конвективными зонами не учитывалась зависимость молекулярного веса от плотности и температуры, т. е. принималось ξ = η. При этом (4.78) записывается в виде

$p = \Pi_4 t^{\frac{5}{2}}.$ (4.79)

где безразмерный комплекс Π₄, обычно обозначаемый через Е, можно записать через безразмерный комплекс Π_5/3 конфигурации, в которой уравнение состояния р ∼ ρ^5/3 имеет место по всей массе:

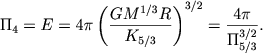
$\Pi_4 = E = 4\pi\left(\frac{GM^{1/3}R}{K_{5/3}}\right)^{3/2} = \frac{4\pi}{\Pi_{5/3}^{3/2}}.$ (4.80)

Отсюда сразу следует, что в полностью конвективной звезде, где Π_5/3 = 0,424, значение параметра Е равно 4π/(0,424)^3/2 = 45,5. Если в (4.78) Π_5/3 < 45,5, то конвективная зона занимает только часть радиуса.

Теперь постановка задачи по построению модели звезды с конвективной зоной заключается в следующем. Система уравнений (4.59) (с учетом (4.72) в зоне конвекции) и выражения (4.60) - (4.71) для безразмерных комплексов остаются прежними. В условии (4.62) лучевым давлением можно пренебречь, поскольку в низкотемпературных звездах с поверхностной конвективной зоной оно мало, т. е. можно принять Π₃ = 0. Граничное условие в центре остается прежним (т. е. при x = 0 имеем q = l = 0, р и t - конечны). Граничное условие на поверхности меняется. Теперь следует считать, что при x = 1

$q = 1, \quad l = 1, \quad \sigma = 0, p = Et^{5/2}.$ (4.81)

Зависимость р = Et^5/2 продолжается в глубь до тех пор, пока лучистый градиент температуры, определенный в системе (4.59), не станет меньшим адиабатического градиента (4.73).

И в этом случае величины Π₁ и Π₂ являются собственными значениями системы уравнений, но теперь они зависят от выбранного значения безразмерного комплекса Π₄ = E. Подобными являются модели с одинаковыми значениями параметра Е. Иными словами, подобными являются звезды, у которых величина K_5/3 = р/ρ^5/3 пропорциональна M^1/3R. К сожалению, как уже отмечалось, трудно надежно определить величину K_5/3 на основании теории звездных атмосфер.

Подобные модели звезд с поверхностными конвективными зонами были рассчитаны Шварцшильдом и Остерброком (см. изложение в [1]) для случая поглощения по закону Крамерса и протон-протонного цикла. Учитывая большую плотность газа и меньшую температуру в недрах таких звезд, были приняты следующие значения показателей: α = 0,75 и α = 0,50; ν = 7/2 в законе поглощения и m = 1, n = 4,5 в соотношении для мощности генерации энергии. Результаты определения безразмерных комплексов Π₁ и Π₂, а также нижней границы конвективной зоны x_k и доли массы в лучистом ядре приведены в табл. 4.

Таблица 4

Характеристики модели	Π₄	Π₁	Π₂	x_k	q_k
Модель звезды типа желтого карлика (α = 0,75, ν = 7/2, m=1, n = 4,5)	44,83	3,7 ⋅ 10^-6	7,8	0,413	0,310
	19,66	1,95 ⋅ 10^-6	1,19	0,698	0,914
	5,70	2,42 ⋅ 10^-6	0,198	0,801	0,991
	1,68	2,88 ⋅ 10^-6	0,074	0,871	0,999
Модель звезды типа красного карлика (α = 0,50, ν = 7/2, m=1, n = 4,5)	37,67	5,86 ⋅ 10^-6	4,92	0,558	0,636
	16,82	5,86 ⋅ 10^-6	0,074	0,676	0,913
	8,02	6,35 ⋅ 10^-6	0,0155	0,723	0,971

Как и следовало ожидать, уменьшение безразмерного комплекса Π₄ уменьшает массу и толщину конвективной зоны. Численные значения безразмерных комплексов Π₁ и Π₂ того же характерного порядка, что и у звезд с конвективным ядром, хотя они, конечно, и заметно различаются.

У Солнца, принадлежащего к звездам типа желтого карлика, величина параметра Е невелика (находится, по-видимому, между единицей и десятью), поэтому конвективная зона неглубокая.

Очень протяженные конвективные зоны имеются у красных гигантов. Здесь величина параметра Е достигает обычно 25. Однако сложная структура этих звезд, состоящих из частично вырожденных изотермических ядер, топких слоевых источников энергии, зон лучистого и зон конвективного переноса, затрудняет исследования подобия моделей этого типа звезд. Обычно для расчета таких моделей делают какие-либо предположения, не позволяющие определить их подобие в явном виде. Например, в известных расчетах Шварцшильда (см. [1]) вместо нахождения безразмерного комплекса Π₂ просто задавалась температура газа в слоевом источнике энергии (T = 2 ⋅ 10^-7 градусов). Существенная неопределенность связана и с определением радиуса звезд с очень протяженными конвективными оболочками.

Роль конвекции велика и у сжимающихся протозвезд. Первоначально предполагалось, что в сжимающихся протозвездах энергия переносится излучением. Основанием для такого предположения была сравнительно слабая зависимость мощности выделения энергии от температуры и плотности при гравитационном сжатии. В первом приближении при гомологическом (однородном) сжатии имеем

$\epsilon = \epsilon_0 T,$ (4.82)

т. е. m = 0 и n = 1. Такая слабая зависимость ε от Т уменьшает градиент температуры, а следовательно, приводит к конвективной устойчивости. Однако вещество протозвезд при низкой ионизации и наличии молекул, по-видимому, обладает низкой прозрачностью и поэтому можно ожидать, что здесь энергия все же переносится конвекцией. Согласно предположению Хаяши ([19]) принято считать, что в сжимающихся протозвездах энергия в основном переносится конвекцией и только на более поздних стадиях сжатия более массивных протозвезд в их центральных частях образуются лучистые ядра.

Условие подобия для протозвезды, в которой энергия переносится только излучением, нетрудно получить описанным выше методом с использованием формулы (4.82). В пренебрежении лучевым давлением (Π₃ = 0) и конвективным переносам в поверхностных слоях (Π₄ = 0) можно найти значение безразмерных комплексов Π₁ и Π₂ (см. [1]):

$\Pi_1 = 1,88 \cdot 10^{-6}, \quad \Pi_2 = 1,19.$ (4.83)

Так же сравнительно просто рассчитываются методом предыдущего параграфа полностью конвективные сжимающиеся протозвезды. Здесь Π₄ = Е = 45,5. Величина K_5/3 должна быть определена из полной светимости протозвезды и анализа условий на ее поверхности. Это сделать очень сложно, поскольку температура поверхностей протозвезд низка и вычисление непрозрачности довольно неопределенно. Сжимающиеся модели с конвективными оболочками и ядрами с лучистым переносом энергии были рассчитаны Хаяши и его сотрудниками (см. [19] и статью Хаяши в [10]).

<< § 4.3 Белые карлики и нейтронные звезды | Оглавление | § 4.5 Численное моделирование эволюции звезд >>

Мнения читателей [4]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

$\lg R = \frac{(2+\alpha+m)\eta-(4+\nu-n)(2-\xi)}{(4+3\alpha+3m)\eta+(4+\nu-n)(3\xi - 4)} \lg M + const,$	(4.66)
$\lg L = \left[1+m+\frac{2-\xi}{\eta}n+\frac{[(2+\alpha + m)\eta - (4+\nu - n)(2-\xi)][(3\xi - 4)n - 3m\eta]}{\eta[(4+3\alpha + 3m)\eta + (4+\nu -n)(3\xi-4)]}\right]\lg M + const.$	(4.67)