Астронет > Размерности и подобие астрофизических величин

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Размерности и подобие астрофизических величин << § 2.2 Взаимодействие электромагнитного излучения и вещества | Оглавление | § 3.1 Соотношение масса — светимость >>

§ 2.3 Характерные параметры твердых планет

В последующих главах мы рассмотрим много астрофизических явлений, в которых существенную роль играют и гравитация и электромагнитное излучение. Будут встречаться и другие явления, где важную роль играют крупномасштабные магнитные поля. Но есть еще одна группа астрофизических явлений, где также одинаково важны и гравитация и электростатическое взаимодействие. Речь идет о планетах, состоящих из твердого вещества. В самом деле, структура твердых тел, так же как и атомов и молекул, определяется квантовыми свойствами заряженных микрочастиц. Очевидно, что свойства планет, построенных из твердого вещества, должны зависеть как от гравитации, так и от зарядов и масс протонов и электронов.

Соберем все определяющие параметры. Гравитационные свойства характеризуются постоянной тяготения G, массой М и радиусом планеты R. Кроме того, гравитационные свойства вещества определяются и средним атомным весом ядер, который мы здесь обозначим через А (так что масса ядер равна Аm_р).

С другой стороны, электростатическое взаимодействие электронов и ядер с учетом квантовых свойств можно описать характерным размером атомов и их энергией. Размер атомов порядка боровского радиуса a₀, а энергия также порядка энергии ионизации атома водорода χ_H (см. формулы (1.32)). Правда, у атомов твердых тел, составляющих основную массу планет, размеры в несколько раз больше a₀, а энергия заметно меньше χ_H и это надо учитывать в тех соотношениях, которые мы будем получать ниже.

Итак, имеем следующий набор определяющих параметров: G, М, R, Аm_р, a₀ и χ_H. Можно и здесь составить матрицу размерности, но мы поступим несколько иначе. Планета находится в равновесии, поскольку гравитационная энергия единицы объема планеты, которую можно назвать и гравитационным давлением, сравнима с сопротивлением сжатию со стороны вещества планеты. Из формулы (2.28) сразу следует для среднего гравитационного давления:

$p \approx \frac{U}{\frac{4\pi}{3}R^3} \approx \frac{3}{4\pi}\frac{GM^2}{R^4}.$ (2.67)

Гравитационное давление в центральных частях планеты, очевидно, может быть больше среднего в десятки раз.

Сопротивление вещества сжатию характеризуется модулем упругости С, согласно соотношению

$p = C\frac{\Delta V}{V},$ (2.68)

где ΔV/V - относительное уменьшение объема под действием давления р. Величину модуля упругости, имеющую размерность эрг/см³, можно сразу выразить через атомные параметры a₀ и χ_H (см. [6]). Имеем

$C \sim \frac{\chi_H}{a_0^3} \sim \frac{m_e^4 e^{10}}{\hbar^8}.$ (2.69)

Однако, учитывая сказанное выше об истинных размерах и энергиях вещества планет, можно утверждать, что здесь есть численный множитель, заметно меньший единицы. В самом деле, численная величина отношения

$\frac{\chi_H}{a_0^3} \approx 1,7 \cdot 10^{11} \frac{\mbox{эрг}}{\mbox{см}^3},$

то время как модули упругости реальных твердых тел в лабораторных условиях C ≈ 10¹¹ - 10¹² эрг/см³. Правда, в недрах планет вещество сжато сильнее, чем на поверхности. .Учитывая также, что и ΔV/V не слишком мало, можно написать следующую оценочную формулу для давления вещества планет, противостоящего гравитационному сжатию:

$p \approx 10^{-1}\frac{\chi_H}{a_0^3} .$ (2.70)

Теперь следует приравнять давление (2.70) гравитационному давлению в недрах планеты. Поскольку мы пока не можем оценить гравитационное давление в центре планеты, примем его просто равным GM²/R⁴. Тогда приравняем эту величину (2.70) и находим:

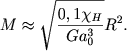
$M \approx \sqrt{\frac{0,1\chi_H}{Ga_0^3}}R^2 .$ (2.71)

Отсюда, кстати, следует, что в рамках этой модели ускорение силы тяжести на поверхности планет определяется только универсальными постоянными:

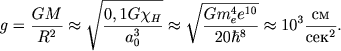
$g = \frac{GM}{R^2} \approx \sqrt{\frac{0,1G\chi_H}{a_0^3}} \approx \sqrt{\frac{Gm_e^4 e^{10}}{20\hbar^8}} \approx 10^3 \frac{\mbox{см}}{\mbox{сек}^2}.$ (2.72)

Как известно, ускорение силы тяжести на поверхности планет земного типа (Меркурий, Венера, Земля, Марс, Уран, Нептун, Плутон) меняется в пределах от 360 до 1500, т. е. не так сильно отличается от (2.72). В рамках столь грубой модели можно считать неплохим согласие, которое к тому же можно улучшить подбором численных множителей.

Из соотношения (2.71) можно исключить R, если воспользоваться определением средней плотности:

$\bar\rho = \frac{3M}{4\pi R^3} \approx \frac{Am_p}{(5a_0)^3}.$ (2.73)

Здесь Am_p - масса, приходящаяся на один атом, который, по предположению, занимает ячейку размером 5a₀=2,5 Å. Множитель пять выбран так, чтобы $\bar\rho$ из (2.73) не слишком расходилось бы с данными наблюдений. Величина A у планет земной группы, вероятно, около 50.

Исключая R из (2.71) и (2.73), находим:

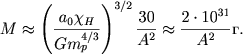
$M \approx \left(\frac{a_0\chi_H}{Gm_p^{4/3}}\right)^{3/2} \frac{30}{A^2} \approx \frac{2 \cdot 10^{31}}{A^2}\mbox{г}.$ (2.74)

При A ≈ 50 масса планеты M ≈ 8 ⋅ 10²⁷ г, что не слишком сильно отличается от массы Земли - 6 ⋅ 10²⁷ г.

Таким же путем определяется и радиус планеты. Имеем

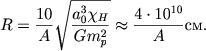
$R = \frac{10}{A}\sqrt{\frac{a_0^3\chi_H}{Gm_p^2}} \approx \frac{4 \cdot 10^{10}}{A}\mbox{см}.$ (2.75)

При A = 50 получаем для радиуса планеты 8 ⋅ 10³ км, что также неплохо согласуется с радиусом Земли.

Аналогичные соображения были использованы Вайскопфом [6] для оценок высоты гор и длины морских волн на поверхности Земли. Высота гор определяется из следующего условия: потенциальная энергия одной молекулы на вершине горы не должна быть больше теплоты плавления вещества (в расчете на одну молекулу) у основания горы, иначе она "утонет". Потенциальная энергия есть Am_pgH, где H - высота горы, а теплота плавления опять характеризуется величиной χ_H, но с некоторым малым множителем - по оценке Вайскопфа типичная теплота плавления в расчете на одну молекулу близка к 10^-2χ_H. Отсюда для высоты гор имеем оценку:

$H \approx 10^{-2} \frac{\chi_H}{Am_p g}.$ (2.76)

Если подставить сюда значение А ≈ 50 и g ≈ 10³ см/сек², то получим H ≈ 26 км. То, что значение (2.76) оказалось несколько больше действительного значения, легко объяснить - горы будут опускаться еще до расплавления основания из-за пластичности пород.

Очевидно, что в определении радиуса планеты и высоты гор использовано одно и то же явление - уравновешивание гравитационного притяжения сопротивлением вещества сжатию или расплавлению, обязанному электростатическим силам в атомах и молекулах. Поэтому R из (2.75) и H из (2.76) одинаковым образом зависят от универсальных констант; различие лишь в численных множителях, описывающих, с одной стороны, сжатие вещества при очень высоких давлениях, а с другой стороны, - его расплавление или пластичность при более умеренных давлениях. Если подставить в (2.76) выражение (2.72) и считать, что атомные веса горных пород и недр Земли сравнимы, то получим H ≈ 3 ⋅ 10^-3R.

Вероятно, формула (2.76) имеет большую область применимости - при ее выводе не использовались несколько неопределенные данные о давлении в недрах планет и о свойствах вещества. Численный множитель в (2.70) оценен очень грубо. Возможно, что он существенным образом зависит от состояния вещества и поэтому может быть различен у разных планет. В (2.76) эта неопределенность слабее и поэтому формулу (2.76) можно использовать и для оценки высоты гор на планетах с разными условиями. Рассмотрим, например, планеты с одинаковой средней плотностью. Тогда ускорение силы тяжести на поверхности этих планет

$g = \frac{GM}{R^2}. = \frac{4\pi}{3}G\bar\rho R.$ (2.77)

Подставляя (2.77) в (2.76), находим

$HR \approx 2,5 \cdot 10^{-3} \frac{\chi_H}{Am_pG\bar\rho} \approx 4,9 \cdot 10^5 \mbox{км}^2,$ (2.78)

если принять A ≈ 50 и $\bar\rho$ &assymp 2 г/см³. Отсюда следует, что перестают быть сферическими планеты с размером меньшим 700 км, т. е. малые планеты Солнечной системы. Возможно, что соотношение (2.78) определяет и верхний предел размеров осколков при разрушении планет.

Для определения длин волн (λ) на поверхности моря Вайскопф [6] использовал следующие соображения. Ветер возбуждает в первую очередь волны с наименьшей фазовой скоростью, а тогда λ на поверхности моря определяется поверхностным натяжением σ . Имеем

$\lambda \approx \sqrt{\frac{\sigma}{g\rho}}.$ (2.79)

Поверхностное натяжение есть энергия на единицу площади, т. е. в атомных величинах в $\sigma \sim \frac{\chi_H}{a_0^2}$ . Принимая здесь также $\rho \sim \frac{m_p}{a_0^3}$ , получим

$\lambda^2 \approx 3 \cdot 10^{-3} \frac{a_0\chi_H}{m_pg},$ (2.80)

где численный множитель соответствует волнам на поверхности воды.

Итак, как подчеркивает Вайскопф [6], даже длина морских волн есть следствие "соревнования" между гравитационным взаимодействием и атомными электростатическими силами.

<< § 2.2 Взаимодействие электромагнитного излучения и вещества | Оглавление | § 3.1 Соотношение масса — светимость >>

Мнения читателей [4]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце