Звездные скопления << 9.8 Использование ЭВМ для решения проблемы динамической эволюции звездных скоплений | Оглавление | 10.2 Функции светимости звезд в шаровых скоплениях и массы этих систем >>

---

Глава 10. Функции светимости звезд в звездных скоплениях и массы этих систем

"Что же делать, если обманула
Та мечта, как всякая мечта..."
А. Блок, Перед судом.

"Так мало пройдено дорог
Так много сделано ошибок!"
С. Есенин, Мне грустно на тебя
смотреть...

10.1 Функции светимости звезд в рассеянных скоплениях

  a) Начальная функция светимости. Проблема белых карликов. Функция светимости φ(М), т. е. распределение звезд данной системы по абсолютным звездным величинам, определяется выражением ср (M)dM, дающим число звезд в единице объема системы, абсолютные величины которых заключены между М и М + dM.

До середины 50-х годов функции светимости служили лишь для характеристики звездного состава тех или иных систем и для сравнения последних между собою. В случае рассеянных скоплений эти функции вообще определялись, как правило, только для ядерных областей скоплений. В случае шаровых скоплений область определения φ(М) до сих пор выбирается довольно произвольно.

Массовые определения функций светимости в звездных скоплениях начались лишь в середине 50-х годов, когда вопросы возникновения и эволюции звезд стали интересовать многих исследователей и появилась реальная надежда выяснить эти вопросы путем непосредственных наблюдений. Именно тогда окрепло убеждение в том, что функция светимости может отражать особенности физической и динамической эволюции системы или особенности процесса звездообразования.

В 1957 г. были опубликованы три статьи Сэндиджа (1957а; 1957б; 1957в), посвященные так называемому наблюдательному подходу к проблеме эволюции. Диаграмма Херцшпрунга - Рессела, или М_bol, lgT_e звезд скопления, члены которого, как предполагается, возникли практически одновременно, не показывает отдельные пути (треки), которые проходят на ней звезды разных масс по мере увеличения их возраста, а является изохроной - геометрическим местом точек, соответствующих положению на этих путях отдельных звезд одинакового возраста в данный момент времени. Сэндидж показал, как можно получить эти пути полуэмпирическим способом, исходя из вида диаграммы М_bol, lgT_e звезд скопления, знания их функции светимости и теории начальной эволюции звезд главной последовательности - до предела Шенберга - Чандрасекара.

Допустим, что существует независимая от времени функция ψ(М_V), которая описывает начальное распределение светимостей в звездном скоплении сразу же после его образования, когда все звезды еще лежат на начальной главной последовательности. С течением времени, по мере того как звезды будут покидать главную последовательность, вид функции светимости звезд скопления будет меняться. Можно допустить, что общая функция светимости звезд в галактическом поле есть сумма видоизмененных вследствие эволюции функций светимости звездных подсистем разного возраста. Используя теорию эволюции звезд с постоянной массой при отсутствии перемешивания и предположив, что скорость образования звезд в окрестностях Солнца оставалась постоянной в течение существования Галактики, Салпитер (1955) вывел уравнение, позволяющее по наблюдаемой общей функции светимости Φ(М_V) звезд поля в окрестностях Солнца найти начальную функцию светимости звезд главной последовательности ψ(М_V). Впоследствии значения этой функции были уточнены Сэндиджем (1957а).

На рис. 145 (Сэндидж, 1957а) функции светимости, наблюдаемые в нескольких рассеянных скоплениях разного возраста, сопоставлены с общей функцией светимости звезд поля Φ(М_V) по данным ван Рейна (прерывистая кривая) и начальной функцией светимости ψ(М_V), изображенной сплошной кривой. Видно, что Φ(М_V) не совпадает с ярким концом функций светимости звезд в рассеянных скоплениях. В молодых скоплениях ярких звезд больше.

С другой стороны, начальная функция светимости ψ(М_V) достаточно хорошо согласуется с наблюдаемым распределением светимостей звезд в рассеянных скоплениях. Поскольку эти скопления (кроме М 67) сравнительно молоды, отсюда можно сделать вывод о том, что ψ(М_V) действительно одинакова для всех недавно возникших систем и может считаться достаточно хорошо известной.

Рис. 145. Функции светимости звезд пяти рассеянных скоплений (Сэндидж, 1957а). Сплошная и прерывистая кривые - нормализованные начальная функция светимости и общая функция светимости звезд поля.

Опираясь на это, Сэндидж (1957а) предложил метод для нахождения числа ярких звезд главной последовательности, существовавших первоначально в каждом из рассматриваемых скоплений, но покинувших главную последовательность в результате эволюции. Метод состоит в подсчете числа звезд N₀, соответствующего свободной от звезд площади под кривой ψ(М_V), продолженной до пересечения ее с осью абсцисс. Кривая ψ(М_V) нормализуется при этом так, чтобы она совпадала с наблюдаемой функцией светимости звезд скопления φ(М_V) в районе соответствующем точке поворота главной последовательности скопления.

Ушедшие с главной последовательности звезды скопления переходят в область красных гигантов, а затем, по-видимому, сбрасывая оболочку, превращаются в белых карликов. В таком случае N₀ = N_g + N_wd, где N_g и N_wd - числа наблюдаемых в скоплении гигантов и белых карликов соответственно. Чем старше скопление, тем больше в нем (с этой точки зрения) должно быть белых карликов. Соответствующие наблюдениям числа N₀, N_g и N_wd Для ряда скоплений приведены в табл. 10.1 по современным данным, а для М 67 - по данным Бааде (1966, с. 131).

Скопление	N0	Ng	Nwd	mlim
h Per	0	-	-	-
Плеяды	2	0	0	25,5
Волосы Вероники	9	1	?	24,5
Гиады	23	4	7	23,0
Ясли	20	4	4	26,0
M 67	146	20	30	29,5

Абсолютные величины M_pg белых карликов заключены в пределах от +8^m до > +20^m, при 〈M_pg〉 ≈ 12^m. В столбце m_lim табл. 10.1 приведены величины, до которых должны быть изучены данные скопления для полного выявления в них белых карликов. Ясно, что в настоящее время можно только мечтать об исчерпывающем анализе физического состава рассеянных скоплений. И тем не менее поиски хотя бы наиболее ярких белых карликов в широких районах рассеянных скоплений представляют огромный интерес. К сожалению, поиски эти крайне трудоемки, а результаты их весьма неуверенны. Бааде, нашедший в центральной части скопления М 67 около 30 слабых голубых звезд (от 20^m до 22^m,7 pg), высказал убеждение, что полное число белых карликов в этом скоплении вполне может достигать 150-200.

Сэндидж (1957а) считал, что числа слабых белых звезд, наблюдаемых в районах рассмотренных им скоплений, не противоречат его концепции. Однако в ряде случаев мы не знаем собственных движений и показателей цвета предполагаемых белых карликов, не знаем даже истинных угловых размеров скоплений, в которых они разыскиваются. Как правило, нигде не приводится доказательств реальной принадлежности белых карликов к соответствующим скоплениям путем установления хотя бы факта концентрации этих объектов в объеме того или иного скопления по сравнению с окружающим полем.

Только в работах Люйтена (1960; 1961; 1962) произведено сравнение чисел слабых белых звезд, наблюдаемых в районах рассеянных скоплений, с соответствующими числами, полученными для контрольных областей. Люйтен (1961) показал, что в контрольных областях наблюдается обычно столько же возможных белых карликов, сколько их встречается в районах изученных им скоплений.

Наличие у скоплений корональных областей, содержащих подавляющее большинство слабых членов скоплений, заставляет с большой осторожностью относиться ко всем выводам, основанным на сравнении районов скоплений (как правило, ядерных) с так называемыми контрольными областями. Однако и определения собственных движений, позволяющие выделить из большого числа слабых белых звезд, наблюдаемых в районах близких скоплений, возможные члены этих систем, показывают, что в скоплениях наблюдается гораздо меньше белых карликов, чем следует из расчетов Сэндиджа. Так, в Гиадах и Яслях вместо 19 и 16 белых карликов, предсказываемых Сэндиджем, открыто пока соответственно лишь 7 и 4 (Люйтен, 1960; 1962; см. также § 3.7). Не доказано также, что в скоплении Волосы Вероники содержится хотя бы один из тех восьми белых карликов, которые должны находиться в нем согласно Сэндиджу. Правда, мы еще далеко не достигли при изучении этих скоплений тех предельных величин, которые указаны в табл. 10.1.

Проблема наличия белых карликов в скоплениях интересна и с точки зрения проверки современных представлений о судьбе звезд, массы которых превышают 1,5 - 3 массы Солнца, после истощения в них запасов ядерной энергии. Если эти звезды, коллапсируя, превращаются и черные дыры, то при подсчете числа белых карликов в скоплениях следует ограничиться звездами с массами меньше 1,2 солнечной.

  б) Значение функций светимости для формирования современных представлений об эволюции звезд. Особую роль сыграли функции светимости при определении эволюционных путей звезд скоплений на диаграмме М_bol, lgT_e по методу, предложенному Сэндиджем (1957в) для объяснения наблюдаемых диаграмм М_V, В - V звезд старых рассеянных и шаровых скоплений.

Функция светимости звезд очень старого рассеянного скопления М 67 (см. рис. 145) заметно отличается от других, изображенных на том же рисунке, очень узким максимумом и резким падением с переходом к более слабым величинам. Ван ден Берг (1957б) объяснил это явление тем, что наименее массивные звезды уже покинули скопление, так как его возраст в 180 раз больше времени релаксации системы. Работа ван ден Берга показала важность учета факторов динамической эволюции скоплений при сравнении между собой функций φ(М_V) и ψ(М_V). Ван ден Берг рассчитал для ряда интервалов М_V и соответствующих им масс звезд скопления М 67, какая доля этих звезд f(М_V) останется в скоплении по истечении 180 времен релаксации. Оказалось, что значения f(М_V) = 1,000 при -0^m,25 < М_V < +3^m,75, а затем быстро убывают с уменьшением светимости звезд. Теперь, после появления работы Вилена (1967), показавшего независимость доли звезд, покидающих скопление, от их массы (см. § 9.8), мы вправе сомневаться в правильности заключения ван ден Берга, но тогда оно считалось бесспорным.

Рис. 146. Наблюдаемая функция светимости Φ(М_V) для скопления М 67 и начальная функция светимости fψ(М_V), исправленная за эффект ухода из скопления звезд малой массы (Сэндидж, 1957в)

Рис. 147. Полуэмпирические эволюционные треки звезд в скоплении М 67 (Сэндидж, 1957в).

На рис. 146 (Сэндидж, 1957в) рядом с наблюдаемой функцией светимости Φ(М_V) звезд скопления М 67 показана его начальная функция светимости, видоизмененная для звезд слабее М_V = + 3^m,75 с учетом потери их скоплением за время его существования: f(М_V)ψ(М_V). Для нормализации этой функции использовано соотношение

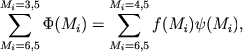
(10.1)

вытекающее из рис. 147 (Сэндидж, 1957в), на котором тонкими кривыми изображены эволюционные треки звезд главной последовательности. Жирными линиями схематически представлена наблюдаемая диаграмма М_bol, lgT_e звезд скопления М 67. Линия SC пересекает эволюционные треки в точках, соответствующих пределу Шенберга - Чандрасекара. Трек 10 - SC соответствует звезде, проэволюционировавшей от точки 10 на начальной главной последовательности с М_bol = +4^m,5 до точки поворота нынешней главной последовательности звезд М 67 с М_bol = +3^m,5. К этому моменту все звезды скопления, находившиеся на начальной последовательности ниже точки 10 (в диапазоне + 4^m,5 < М_bol < +6^m,5), еще не достигнут своего предела Шенберга - Чандрасекара и окажутся на наблюдаемом сейчас отрезке главной последовательности скопления ниже ее точки поворота (в диапазоне +З^m,5 < М_bol < +6^m,5). Этим и определяется соотношение (10.1), отражающее равенство заштрихованных на рис. 146 площадей.

Все звезды, наблюдаемые на диаграмме М_bol, lgT_e выше линии SC, возникли из звезд начальной главной последовательности, лежавших выше точки 10. Их эволюционные пути до достижения линии SC рассчитаны теоретически. Далее следует экстраполяция этих путей за предел Шенберга - Чандрасекара, т. е. процедура, благодаря которой описываемый метод получения эволюционных путей звезд назван полуэмпирическим.

Скорость эволюции тем выше, чем массивнее звезда. К моменту, когда звезды из точки 10 достигли линии SC, звезды из точки 11 уже прошли SC и достигли точки a, а звезды из точки 12 достигли точки b. Число звезд, наблюдаемых сейчас на отрезке жирной линии между SC и а, равно числу звезд, бывших ранее на отрезке начальной главной последовательности между точками 10 и 11; число звезд между aи b равно числу звезд между точками 11 и 12, и т. д. Числа звезд на отрезках -наблюдаемой последовательности SC - а - b - ... задаются известной нам функцией Φ(М_V). Расстояния же между соответствующими им точками 10 - 11 - 12 - ..., определяющими отрезки начальной главной последовательности, содержащие в точности те же числа звезд, находятся из рис. 146 с помощью уже функции f(М_V)ψ(М_V). При этом, конечно, используются обычные соотношения между значениями В - V и lgT_e и болометрические поправки для перехода от М_V к М_bol в зависимости от В - V.

При таком рассмотрении оказывается, что все звезды скопления, наблюдаемые сейчас выше точки SC, произошли из звезд главной последовательности с +З^m,84 < М_bol < +4^m,4, т. е. из звезд, М_bol которых различались всего лишь на 0^m,56, а массы наиболее массивных из них, в соответствии с соотношением масса - светимость, могут превышать массы наименее массивных не более, чем в 1,1 раза. Подобные расчеты были проведены Сэндиджем (1957в) также для шарового скопления М 3.

Эти расчеты полностью согласуются с выводами современной теории звездной эволюции и не оставляют места сомнениям в правильности этой теории. В настоящее время можно было бы не вспоминать об умозрительных гипотезах, допускавших возможность значительных различий масс звезд, расположенных вдоль ветвей субгигантов и красных гигантов в старых рассеянных и шаровых скоплениях (Пэйн-Гапошкина, 1952; Холопов, 1965в; 1965г). К сожалению, такие гипотезы высказывались, и теперь мы должны признать их несостоятельность.

Рис. 147 существенно устарел лишь в отношении изображения эволюции звезд горизонтальной ветви (см. § 6.8).

  в) Функции светимости звезд в ядерных и корональных областях рассеянных скоплений. Представленные на рис. 145 функции светимости соответствуют разным объемам скоплений. В Плеядах рассмотрена область радиусом 1°; вокруг центра (область ядра), в Гиадах - весь объем скопления, в Яслях - область ядра, в скоплении М 67 - область радиусом 10' (в 1,3 раза превышающим радиус ядра скопления).

В дальнейшем изучаемые области скоплений постепенно расширялись. В работе ван ден Берга и Шера (1960) рассмотрены функции светимости в 20 рассеянных скоплениях, причем радиус скопления М 67 был принят равным уже 28',5, в отличие от 4',8, принимавшегося ранее ван ден Бергом (1957б). Время релаксации М 67 в этой работе принимается уже на порядок больше принимавшегося ван ден Бергом, что значительно уменьшает число звезд, потерянных скоплением за время его существования. Соответственно нуждается в изменении и рис. 146 (Сэндидж, 1957в). Ван ден Берг и Шер получили новые функции светимости для всего объема М 67 и для внутренней его области радиусом 8',5.

Вскоре Шер (1962) проанализировал данные, полученные в этой работе, более детально. Шер разбил скопление на три области: 1 (0 < r < 5',7), 2 (5',7 < r < 14',25) и 3 (14',25 < r < 28',5), - и построил функции светимости отдельно для трех объемов скопления, соответствующих этих областям. При этом было учтено влияние функций светимости внешних областей на функции светимости более внутренних, обусловленное проекцией внешних объемов на внутренние. Учет влияния звезд фона производился с помощью подсчетов звезд разной величины в области от 28',5 до 51',3 от центра системы.

Полученные Шером функции светимости для всех трех областей имеют максимум при 14^mpg. Но в то время как в центральной области после этого максимума число звезд по мере уменьшения их блеска уменьшается и при 19^mpg доходит до нуля, во второй и третьей областях падение φ(М) практически прекращается уже при 17^m. В этой работе Шера с исключительной наглядностью продемонстрировано изменение функции светимости звезд в скоплении М 67 с изменением расстояния от его центра. Тогда же подобные явления в скоплениях были проанализированы Стариковой (1962), в основном по данным, опубликованным ван ден Бергом и Шером (1960).

В 1961 г. Артюхина и Холопов (1961) детально изучили распределение звездной плотности в скоплении М 67. Средний радиус скопления оказался равным 54'. Так как это значение почти вдвое превосходит значение, принятое в работах ван ден Берга и Шера, ясно, что полученные последними авторами выводы о свойствах функции светимости в М 67 нуждаются в ревизии. Достаточно отметить, что область, избранная ими для анализа распределения величин звезд фона, оказалась фактически областью короны скопления.

Рис. 148. Функции светимости звезд в скоплении М 67: (a) - в короне скопления, (b) - в промежуточной области, (с) - в ядре, (А) - во всем скоплении (Холопов, Артюхина, 1964); (F) - распределение величин звезд фона в районе скопления М 67.

На рис. 148 изображены функции светимости звезд в М 67, полученные Холоповым и Артюхиной (1964). На рис. 148А - для всего объема скопления, на рис. 148а - для области короны скопления (от 22',5 до 64',7 от центра), на рис. 148b - для промежуточной области (от 7'5 до 22',5 от центра), на рис. 148с - для области ядра (от 0 до 7',5 от центра). Рис. 148F показывает распределение звездных величин в области фона (от 65' до 91',5 от центра скопления). Влияние проекции наружных областей системы на внутренние также учтено.

Рис. 148 показывает, что после максимума в районе 14^m, соответствующем точке поворота главной последовательности, наблюдается минимум φ(М) около 15-16^m во всех областях скопления, за которым намечается тенденция к новому возрастанию этой функции, меньшая в области ядра и большая в области короны. Около 11^m,5 наблюдается небольшой максимум, объясняемый наличием звезд горизонтальной ветви и подтверждающий присутствие ярких звезд скопления в короне системы.

Учитывая, что основное количество слабых членов скоплений находится в коронах этих систем, а область короны М 67 до середины 60-х годов принималась за область фона, следует признать, что большинство слабых членов М 67 ранее просто отбрасывалось при определении φ(М). Более того, пренебрежение областью короны приводило к преувеличению плотности фона и к преуменьшению числа членов скопления даже в тех областях, которые считались районами скопления.

Рис. 149. Функция светимости звезд в объеме всего скопления М 67 (Попова, 1972).

На рис. 149 показана полученная Поповой (1972) функция светимости для всего объема скопления М 67 (от 0 до 65' от его центра), полученная по подсчетам звезд на карте Паломарского атласа неба и свидетельствующая о том, что реальный максимум этой функции еще далеко не достигнут. Рассмотрим теперь данные о функции светимости звезд в другом хорошо исследованном скоплении - Плеядах. Эта функция изучалась также неоднократно. Еще Трюмплер (1921) проследил ход функции светимости в Плеядах до M_pg = 8^m. Уже тогда он построил две отдельные функции светимости (для центральной области (ядра) скопления радиусом 1°; и для внешней области от 1°; до 3°; от центра) и обнаружил различие между ними. Функция светимости звезд для внешней (корональной) области скопления была прослежена им до M_pg = + 4^m,5.

Лишь через полвека функция светимости звезд во всем объеме Плеяд была вновь изучена Холоповым и Артюхиной (1971). На рис. 150 представлены графики φ(М) для зоны ядра (радиусом 1°;,1), зоны короны (от 1°;,1 до 3°;,5 от центра) и для всего скопления. В короне этого сравнительно молодого скопления нет звезд ярче M_pg = +1^m, которые содержатся только в ядре системы (факт, отмечавшийся еще Трюмплером), и сравнительно мало звезд с M_pg от + 1 до +4^m. Однако общие черты функций светимости для ядра и короны Плеяд в большом диапазоне величин чрезвычайно сходны. Кривая, представляющая функцию светимости звезд в короне, смещена относительно кривой, соответствующей функции светимости звезд в ядре, примерно на 1^m в сторону меньших светимостей.

Максимум φ(М) в ядре наблюдается при 11^m,5 pg. Ему соответствует первый максимум φ(М) в короне, наступающий не раньше 12^m pg. В районе 14^m pg в ядре наблюдается минимум φ(М), которому соответствует минимум φ(М) звезд короны в районе 15,5-16^m pg. Затем вновь и в ядре и в короне скопления начинается рост функции светимости. Полная масса членов Плеяд ярче М_V = +12^m близка к 400 массам Солнца (Холопов, 1971б).

Рис. 150. Функции светимости звезд в объеме ядра, короны и всего скопления Плеяды (Холопов, Артюхина, 1971).

Сравнение функций светимости звезд в скоплениях Плеяды и М 67 позволяет думать, что по мере увеличения возраста скопления общее сходство функций светимости в его ядре и короне исчезает: в плотном ядре остается все меньше и меньше слабых звезд, которые постепенно переходят в область короны скопления и накапливаются в ней. Потерю звезд ядром не следует отождествлять с потерей звезд скоплением. У очень старых рассеянных и шаровых скоплений функции светимости в ядрах и коронах не могут быть одинаковы, хотя различия между ними не так велики, как представлялось в конце 50-х годов.

---

<< 9.8 Использование ЭВМ для решения проблемы динамической эволюции звездных скоплений | Оглавление | 10.2 Функции светимости звезд в шаровых скоплениях и массы этих систем >>

Публикации с ключевыми словами: звезды - Скопление Публикации со словами: звезды - Скопление
См. также: Черная дыра разрушает звезду: анимация Звезды, пыль и туманность в NGC 6559 25 самых ярких звезд на ночном небе Анимация: черная дыра разрушает звезду Комета, скопления и туманности Сравнение размеров звезд Самая далекая из всех известных звезд? Все публикации на ту же тему >>