9.8 Использование ЭВМ для решения проблемы динамической эволюции звездных скоплений
Появление ЭВМ сразу же позволило поставить задачу проверки выводов, полученных статистическими методами, путем численного интегрирования точных уравнений движения n тел, объединенных в самогравитирующие системы. Точность решения при этом контролируется требованием постоянства общих интегралов движения. При задании начальных координат и скоростей членов системы обычно проверяется выполнение теоремы вириала.
Начало систематическим исследованиям в этом направлении было положено работами Хёрнера (1960; 1963). В первой работе рассматривалась система, состоящая из 16 звезд, во второй - из 25. Начальное распределение плотности принималось однородным, распределение скоростей - максвелловым.
В результате динамической эволюции системы, прослеженной во второй работе до 40 времен релаксации, в ней образовалась центральная область максимальной плотности, содержащая несколько тесных пар звезд. Радиус системы увеличился на три порядка, диапазон плотности достиг девяти порядков. Плотность во внешнем объеме системы оказалась меняющейся по закону (9.44). Распределение скоростей стало отличаться от максвеллова: появился избыток больших и малых скоростей. При этом избыток больших скоростей обусловлен не выбрасыванием из системы звезд со скоростями, превышающими скорость отрыва (их число оказалось меньше теоретического), а появлением в центре скопления тесных пар и групп звезд; избыток малых скоростей - появлением звезд, движущихся близ апоцентров своих орбит на больших расстояниях от центра скопления.
Выводы Хёрнера подтвердил Вилен (1967), изучивший эволюцию трех моделей звездных скоплений, характеризующихся шустеровским законом распределения плотности. Каждая модель состояла из 100 членов. По массам звезды делились на четыре группы, в соответствии с начальной функцией светимости (см. § 10.1) состоявшие из четырех звезд с массой 4,4 солнечных, из 10 звезд с массой 2,2, 24 звезд с массой 1,1 и 62 звезд с массой 0,55 солнечной массы. Две модели были стационарны (одна из них была наделена дифференциальным вращением).
Оказалось, что звезды, покидающие скопление со скоростями отрыва, приобретают эту скорость не постепенно (в результате далеких сближений), а внезапно, вследствие тесного сближения с другой звездой или с небольшой группой звезд. Этот результат явился подтверждением теоретического вывода Энона (1960б) - см. § 9.5. Процент звезд, покидающих скопление, оказался почти не зависящим от массы звезды, не считая того, что наиболее массивные звезды вообще не покидают скопление.
Во внешних областях скопления и даже в областях, близких к ядру, устанавливается радиальное поле скоростей. Стэндиш (1968), а также Арни и Вейссман (1973) показали, что испытывающее гравитационный коллапс скопление с первоначально однородным распределением плотности и нулевыми начальными скоростями не стягивается в точку. По мере приближения к его центру членов, располагавшихся на периферии, более близкие к центру члены уже пересекают центральную область и начинают удаляться от нее. Минимальный радиус скопления, достигаемый в результате коллапса, составляет 0,2-0,3 величины начального радиуса коллапсирующей системы.
Аарсет и Хилс (1972) рассмотрели динамическую эволюцию более сложной модели скопления, состоящей вначале из цепочки субскоплений. Подобная структура наблюдается, в частности, в ассоциации Ориона. Скопление Меч Ориона (см. фронтиспис) состоит из четырех субскоплений (группы HD 37016, группы 42 Ориона, скопления Трапеции и группы i Ориона), расположенных вдоль прямой линии.
Рис. 144 (Аарсет, Хилс, 1972) позволяет проследить за отдельными этапами эволюции рассмотренной ими модели, которую можно назвать моделью протоскопления. На рисунке показаны положения звезд протоскопления в проекции на плоскости XZ и YZ. Первоначальная цепочка субскоплений расположена вдоль оси Z. Звезды пронумерованы в соответствии с их принадлежностью к восьми субскоплениям в начальный момент времени T = 0. Массы их в каждом субскоплении приняты различными (в соответствии с законом масса - светимость и начальной функцией светимости звезд).
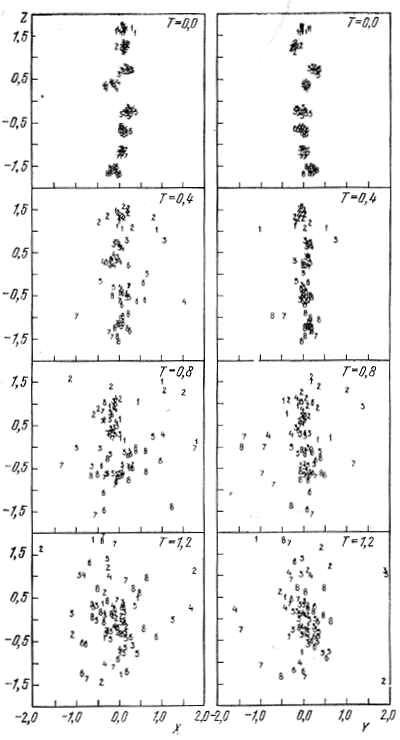
Рис. 144. Динамическая эволюция модели протоскопления состоящего из восьми субскоплений (Аарсет, Хилс, 1972).
Вначале субскопления покоятся относительно друг друга, затем начинается свободное падение звеньев цепочки к центру системы и взаимное сближение членов каждого из субскоплений (начальный коллапс). Временной параметр T на рис. 144 определяется выражением T = t/t0, где t - время, a t0 - промежуток времени от начала эволюции скопления до момента максимального сжатия системы, обусловленного ее начальным коллапсом. При начальной массе протоскопления, равной 120 солнечным массам, и начальной длине цепочки субскоплений, равной двум парсекам, t0 = 3 · 106 лет. В процессе начального коллапса восемь субскоплений сливаются и четыре, затем в два и, наконец, в одно. Одновременно из каждого субскопления выбрасываются звезды за счет образования внутри субскоплений тесных двойных систем.
К моменту слияния всех субскоплений в одно (спустя несколько миллионов лет после начала эволюции) система выглядит уже как типичное звездное скопление, характеризующееся наличием ядра и окружающей его стационарной короны, за пределами которой находятся удаляющиеся от скопления звезды, выброшенные из системы со скоростями, превышающими скорость отрыва. В модели Аарсета и Хилса скопление теряет около одной трети образовавшихся в нем звезд. После достижения динамического равновесия (к моменту T = 2 - 2,5) скорость динамической эволюции скопления заметно замедляется.
Мы видим, что использование ЭВМ позволяет дополнить классическую теорию динамической эволюции квазистационарных звездных скоплений анализом быстро развивающихся динамических явлений, соответствующих первой стадии динамической эволюции звездных систем по Агекяну.
В последнее время увеличивается число звезд в моделях скоплений, рассматриваемых разными авторами. Совершенствование методики вычислений позволяет довести это число до 500 (Вилен, 1974; Аарсет, 1973; 1974). Появляются также работы, в которых учитывается потеря массы членами скоплений, обусловленная их физической эволюцией как на ранней (протозвездной), так и на более поздних стадиях развития.
Однако до сих пор не ясно, до каких пределов можно экстраполировать результаты, полученные для моделей, содержащих небольшое число членов (N < 500), на реальные шаровые скопления, состоящие из десятков и сотен тысяч звезд.
<< 9.7 Динамическая эволюция звездных скоплений | Оглавление | 10.1 Функции светимости звезд в рассеянных скоплениях >>
|
Публикации с ключевыми словами:
звезды - Скопление
Публикации со словами: звезды - Скопление | |
См. также:
Все публикации на ту же тему >> | |