Астронет > Движущиеся оболочки звезд

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Движущиеся оболочки звезд << 5.1 Происхождение "комбинационных спектров" | Оглавление | 5.3 Общие соображения >>

5.2 Оптическая толщина оболочки за границами субординатных серий

В предыдущей главе были указаны три причины, понижающие степень возбуждения и ионизации в оболочке: 1) эффект Доплера, 2) удары второго рода и 3) наличие общего поглощения. При выводе формул (5) был учтен только эффект Допплера. Теперь мы примем во внимание две другие причины.

Третья из этих причин с первого взгляда кажется особенно "опасной". Следует, однако, иметь в виду, что в рассматриваемом случае общее поглощение в оболочке есть не что иное, как поглощение за границей субординатной серии данного атома, а это поглощение убывает с понижением степени возбуждения и ионизации. Следовательно, в этом случае степень возбуждения и ионизации будет падать медленнее, чем это было получено в предыдущей главе (§ 3, б).

Мы снова допустим, что атом обладает только тремя уровнями, и будем исходить из уравнений (IV, 62). Пренебрегая очень малой величиной η₁ и учитывая столкновения, вместо этих уравнений получаем

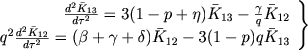
$\left. \begin{array}{r} \frac{d^2 \bar K_{13}}{d\tau^2} = 3(1 - p + \eta)\bar K_{13} - \frac{\gamma}{q} \bar K_{12} \\ q^2 \frac{d^2 \bar K_{12}}{d\tau^2} = (\beta + \gamma + \delta)\bar K_{12} - 3(1-p)q\bar K_{13} \end{array} \right \}$ (23)

Для частей оболочки, достаточно удаленных от границ, отсюда находим

$\frac{d^2 \bar K_{13}}{d\tau^2} = 3\left[\eta + (1-p) \frac{\beta + \gamma}{\beta + \gamma + \delta} \right]\bar K_{13}.$ (24)

Входящая в это уравнение величина η определяется первым из равенств (IV, 61). Обозначая через μ. отношение коэффициента поглощения за границей основной серии, вызванного переходами типа 2 → 3, к коэффициенту поглощения за границей субординатной серии (μ = a'₁₃/a₂₃), и имея в виду соотношение

$\frac{a_{23}}{a_{13}} = \frac{1-p}{p}\frac{\bar K_{13}}{\bar K_{23}} .$ (25)

для величины η имеем

$\eta = \mu \frac{1-p}{p}\frac{\bar K_{13}}{\bar K_{23}} .$ (26)

Но $\bar K_{13} = \frac{1}{4} S_{23}$ . Поэтому, подставляя (26) в (24), получаем

$\frac{d^2 \bar K_{13}}{d\tau^2} = 3\left[4\mu \frac{1-p}{pS_{23}} \bar K_{13} + (1-p) \frac{\beta + \gamma}{\beta + \gamma + \delta} \right]\bar K_{13}.$ (27)

Решение уравнения (27) получается в виде эллиптического интеграла

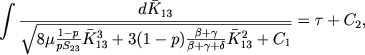
$\int\frac{d\bar K_{13}}{\sqrt{8\mu \frac{1-p}{pS_{23}} \bar K_{13}^3 + 3(1-p) \frac{\beta + \gamma}{\beta + \gamma + \delta} \bar K_{13}^2 + C_1}} = \tau + C_2 ,$ (28)

где C₁ и C₂ - произвольные постоянные. Эти постоянные должны быть определены из граничных условий:

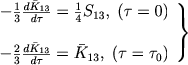
$\left. \begin{array}{r} -\frac{1}{3} \frac{d\bar K_{13}}{d\tau} = \frac{1}{4}S_{13}, \;(\tau = 0) \\ \\ -\frac{2}{3} \frac{d\bar K_{13}}{d\tau} = \bar K_{13}, \;(\tau = \tau_0) \end{array} \right \}$ (29)

Если общее поглощение в оболочке играет бóльшую роль, чем эффект Доплера и столкновения, то решение уравнения (27) при граничных условиях (29) для случая τ₀=∞ имеет вид

$\bar K_{13} = \frac{\frac{3}{4} S_{13}}{\mu\tau_{23}^0 \left(1+\frac{\mu}{2} \tau_{23}^0 \tau \right)} ,$ (30)

где τ₂₃⁰ есть оптическая толщина оболочки за границей субординатной серию. Эта толщина оказывается равной

$\tau_{23}^0 = \left(6 \frac{1-p}{p\mu^2}\frac{S_{13}}{S_{23}}\right)^{\frac{1}{3}} .$ (31)

В противоположном случае решение уравнения (27) получается в форме, полученной нами ранее [см. первую из формул (IV, 32)], а именно:

$\bar K_{13} = \frac{3S_{13}}{4\lambda} e^{-\lambda\tau} ,$ (32)

где

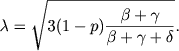
$\lambda = \sqrt{3(1-p) \frac{\beta + \gamma}{\beta + \gamma + \delta}} .$ (33)

Для величины τ₂₃⁰ в этом случае находим

$\tau_{23}^0 = 3 \frac{1-p}{p\lambda^2}\frac{S_{13}}{S_{23}} .$ (34)

Оценим теперь полученные выражения для τ₂₃⁰. Для водородного атома p=1/2, μ=1/64. Поэтому при температуре звезды порядка T_∗=30000°; формула (31) дает для τ₂₃⁰, величину порядка нескольких десятков. При W = 10^-4, n_e = 10¹¹ и β < 10^-6 формула (34) дает для τ₂₃⁰, величину того же порядка. Мы видим, следовательно, что учет столкновений и общего поглощения не понижает значительно оптической толщины оболочки за границей субординатной серии.

Данное нами решение задачи является, однако, не вполне точным, так как при τ₂₃⁰ > 1, величину $\bar K_{23}$ нельзя считать постоянной. Но легко видеть, что в частоте ν₂₃ мы имеем по существу чистое рассеяние. Это значит, что величина $\bar K_{23}$ не может сильно меняться в оболочке. Поэтому и точное решение задачи не может привести к результатам, значительно отличающимся от только что полученных. Мы сейчас дадим это точное решение задачи, для простоты пренебрегая столкновениями и эффектом Доплера.

Вместо одного уравнения (27) мы теперь имеем следующую систему трех уравнений:

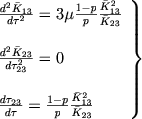
$\left. \begin{array}{l} \frac{d^2 \bar K_{13}}{d\tau^2} = 3\mu \frac{1 - p}{p} \frac{\bar K_{13}^2}{\bar K_{23}} \\ \\ \frac{d^2 \bar K_{23}}{d\tau_{23}^2} = 0 \\ \\ \frac{d\tau_{23}}{d\tau} = \frac{1 - p}{p} \frac{\bar K_{13}^2}{\bar K_{23}} \end{array} \right \}$ (35)

Второе из этих уравнений при граничных условиях аналогичных (29), дает

$\bar K_{23} = \frac{3}{4} S_{23}(\tau_{23}^0 - \tau_{23}) ,$ (36)

из третьего уравнения находим

$\bar K_{13} = -\frac{4p}{3(1-p)} \frac{\bar K_{23}}{S_{23}} \frac{d \bar K_{23}}{d\tau} ,$ (37)

Подставляя (37) в первое из уравнений (35), получаем

$\frac{d^2}{d\tau^2}\left(\bar K_{23} \frac{d \bar K_{23}}{d\tau}\right) = -\frac{4\mu}{S_{23}} \bar K_{23} \left(\frac{d \bar K_{23}}{d\tau}\right)^2 .$ (38)

Это сложное на вид уравнение имеет следующее простое решение:

$\bar K_{23} = \frac{\frac{3}{4} S_2^0 \tau_{23}^0}{1+\frac{\mu}{4} \tau_{23}^0 \tau} ,$ (39)

удовлетворяющее тем же самым граничным условиям (так как должно быть: τ₂₃ = 0 при τ = 0 и τ₂₃ = τ₂₃⁰ при τ = ∞). Подставляя (39)) в (37) и используя условие (29) для определения постоянной τ₂₃⁰, окончательно находим

$\bar K_{13} = \frac{S_{13}}{\mu\tau_{23}^0} \frac{1}{\left(1+\frac{\mu}{4} \tau_{23}^0 \tau \right)^3} ,$ (40)

$\tau_{23}^0 = \left(\frac{16}{3} \frac{1-p}{p\mu^2}\frac{S_{13}}{S_{23}}\right)^{\frac{1}{4}} .$ (41)

Мы действительно видим, что точное решение задачи, даваемое формулами (40) и (41), очень мало отличается от ранее полученного решения, даваемого формулами (30) и (31).

В заключение следует заметить, что выше были учтены только факторы, оказывающие понижающее действие на степень возбуждения и ионизации в оболочке. Существуют, однако, факторы, действующие обратным образом (например удары первого рода). Поэтому приведенные выше оценки величины τ₂₃⁰ являются на самом деле минимальными.

<< 5.1 Происхождение "комбинационных спектров" | Оглавление | 5.3 Общие соображения >>

Публикации с ключевыми словами: оболочки звезд - перенос излучения Публикации со словами: оболочки звезд - перенос излучения
См. также: Сбрасывающая массивную оболочку звезда G79.29+0.46 Обнаружение горячего водяного пара в оболочке углеродной звезды. Оболочки в туманности Яйцо Освещённость Планетарные туманности

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

$\bar K_{13} = \frac{S_{13}}{\mu\tau_{23}^0} \frac{1}{\left(1+\frac{\mu}{4} \tau_{23}^0 \tau \right)^3} ,$	(40)
$\tau_{23}^0 = \left(\frac{16}{3} \frac{1-p}{p\mu^2}\frac{S_{13}}{S_{23}}\right)^{\frac{1}{4}} .$	(41)