4.1 Атом с тремя уровнями
В этом параграфе число ионизованных атомов мы будем обозначать через n3 (вместо n+), а под статистическим весом третьего состояния будем понимать величину
|
|
(1) |
Наряду с шириной спектральной линии Δν12 мы введем эффективные ширины Δν13 и Δν23 . Тогда формально третий уровень ничем не будет отличаться от первых двух. Разница между ними будет только та, что для излучения с частотой ν12 будет иметь значение эффект Доплера, а для излучения с частотами ν13 и ν23 - не будет.
Условия лучевого равновесия мы получим из условий цостоянства числа атомов в каждом из состояний. Для первого и третьего состояний эти условия имеют вид:
|
|
(2) |
Здесь мы пренебрегли переходами, вызванными столкновениями, а также эйнштейновским отрицательным поглощением. Введем теперь величины, обычно употребляемые в теории лучевого равновесия. Пусть aik - объемный коэффициент поглощения, Jik - интенсивность излучения, εik - количество энергии, излучаемое 1 см3 за 1 сек. в единичном телесном угле.
Мы имеем
|
|
(3) |
|
|
(4) |
|
|
(5) |
и уравнения (2) могут быть переписаны в виде:
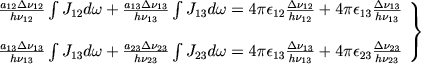
|
(6) |
Естественно ввести здесь величины Kik и Cik, равные
|
|
(7) |
Кроме того, положим
|
|
(8) |
|
|
(9) |
Тогда вместо (6) получаем
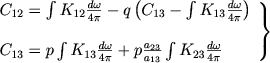
|
(10) |
Так как отношение a23/a13 пропорционально величине C12, то, вообще говоря, второе из этих уравнений является нелинейным. Однако мы уже условились считать, что оптическая толщина оболочки в частоте ν23 меньше единицы. Поэтому величину ρ23 можно считать постоянной.
С помощью вышеприведенных формул легко находим
|
|
(11) |
где использовано одно из обычных обозначений:
|
|
(12) |
Введем еще следующее обозначение:
|
|
(13) |
Тогда, подставляя (11) в (10), окончательно получаем
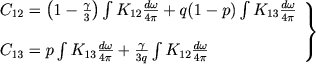
|
(14) |
Таковы условия лучевого равновесия нашей задачи.
Введем оптические расстояния от внутренней границы оболочки в частотах ν12 и ν13:
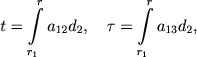
|
(15) |
где r1 и r суть расстояния внутренней границы оболочки и данного слоя от звезды. Обозначим через θ угол между направлением излучения и направлением внешней нормали к слою.
Тогда уравнение переноса излучения в частоте ν13 будет иметь обычный вид
|
|
(16) |
Но для излучения в частоте ν12, для которого играет роль эффект Доплера, в предыдущей главе мы получили более сложное уравнение (III, 17). Считая, что величина β мала, вместо уравнения (III, 17) приближенно находим
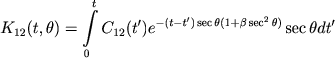
|
(17) |
Отсюда получается следующее уравнение переноса излучения в частоте ν12:
|
|
(18) |
Таким образом наша задача сводится к решению уравнений (14), (16) и (18).
В предыдущей главе, рассматривая лучевое равновесие планетарной туманности в частоте ν12, мы составили интегральное уравнение для величины C12. Теперь, для простоты, мы предпочли получить уравнение переноса (18) и решим задачу обычным методом Эддингтона.
Введем следующие обозначения:
|
|
(19) |
|
|
(20) |
|
|
(21) |
(В последнем уравнении мы пренебрегали величиной β по сравнению с единицей). Эти уравнения с помощью (14) дают:
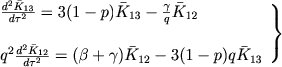
|
(22) |
|
|
(23) |
|
|
(24) |
где λ1 и λ2 суть корни уравнения
|
|
(25) |
а A, B, C, D - произвольные постоянные
В дальнейшем мы будем считать, что
|
|
(26) |
Так как величина q2 очень мала (порядка 10-8), то это условие является выполненным для любой оболочки.
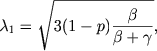
|
(27) |
|
|
(28) |
|
|
(29) |
Чтобы найти произвольные постоянные А, В, С, D, надо задать граничные условия. Эти условия мы задаем в виде
|
|
(30) |
Величина πS13, т.е. число квантов в частоте ν13, падающих от звезды на внутреннюю границу оболочки, равна
|
|
(31) |
Наибольший интерес представляет случай, когда оптическая толщина оболочки в частоте ν13 значительно превосходит единицу (τ0 > 1). В чтом случае для средних частей оболочки мы легко получаем
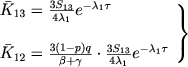
|
(32) |
(так как остальные члены, входящие в выражения для ![]() и
и ![]() , играют лишь роль поправок вблизи границ). Подставляя (32) в (14), для C12 и C13 находим
, играют лишь роль поправок вблизи границ). Подставляя (32) в (14), для C12 и C13 находим
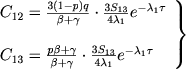
|
(33) |
Знание величин C12 и C13 позволяет найти степень возбуждения и ионизации в оболочке, т. е. величины n2/n1 и n3/n1. На основании соотношений (3), (5) и (7), мы имеем
|
|
(34) |
и, подставляя (33) в (34) находим
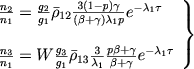
|
(35) |
Обозначим
|
|
(36) |
Тогда формулы (35) преобразуются к виду
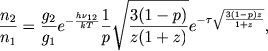
|
(37) |
|
|
(38) |
Эти формулы являются для нас окончательными. Отметим, что в случае неподвижной оболочки т. е. при β = 0, величины ![]() и
и ![]() , а значит, и величины n2/n1 и n3/n1, являются не экспоненциальными, как получилось у нас, а линейными функциями от оптического расстояния.
, а значит, и величины n2/n1 и n3/n1, являются не экспоненциальными, как получилось у нас, а линейными функциями от оптического расстояния.
До сих пор считалось, что в небулярных оболочках степень возбуждения и ионизации зависит от трех величин: от температуры звезды, от коэффициента дилюции и от плотности материи. Теперь мы видим, что она зависит также - и притом весьма сильно - от состояния движения оболочки. Чем больше градиент скорости в оболочке, тем меньше степень возбуждения и ионизации и тем быстрее она падает при переходе от внутренней границы оболочки к внешней.
<< Глава IV. Оболочки новых звезд | Оглавление | 4.2 Реальный атом >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |