3.3 Температуры туманностей и температуры ядер
В предыдущих параграфах мы рассмотрели условия стационарности для первого и второго уровней водородного атома. Теперь мы рассмотрим еще одно условие стационарности - закон сохранения энергии для свободных электронов туманности.
Мы будем предполагать, что свободные электроны получают энергию при фотоионизации водородных атомов, а теряют ее тремя путями:
- при захватах протонами и при free-free transitions;
- при столкновениях, возбуждающих линии N и N "небулия", и
- при неупругих столкновениях с атомами водорода.
Очевидно, что если при математическом представлении этого закона нам удастся ограничиться лишь известными из наблюдений величинами, то мы получим важное соотношение, связывающее температуру центральной звезды и электронную температуру туманности.
Пусть ε - средняя энергия, получаемая электроном при фотоионизации. Так как число ионизации должно равняться числу рекомбинаций, то количество энергии, получаемое электронами в 1 см3 за 1 сек., будет равно ![]() . Часть этой энергии, теряемой при рекомбинациях и free-free transitions, мы обозначим через
. Часть этой энергии, теряемой при рекомбинациях и free-free transitions, мы обозначим через ![]() , другую часть, переходящую в излучение линий "небулия" через E и, наконец, третью часть, расходуемую при столкновениях с водородными атомами, через
, другую часть, переходящую в излучение линий "небулия" через E и, наконец, третью часть, расходуемую при столкновениях с водородными атомами, через ![]() .
.
Закон сохранения энергии дает
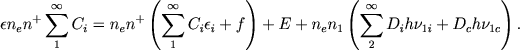
|
(35) |
Здесь нам неизвестна величина Е, ибо мы не знаем ни эффективных сечений для столкновений электронов с атомами OIII, ни концентрации этих атомов. Но эту величину можно найти иначе, если считать известным отношение интенсивностей линий N2/Hβ.
Учитывая, что N1/N2=3, мы имеем
|
|
(36) |
где интегрирование распространяется по всему объему туманности, а ![]() - величина, определяемая из уравнений Cillie(I, 12).
- величина, определяемая из уравнений Cillie(I, 12).
Интегрируя (35) по объему туманности и принимая во внимание (36), получаем
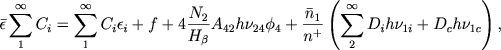
|
(37) |
|
|
(38) |
|
|
(39) |
Величина ![]() есть энергия, получаемая электроном при фотоионизации, средняя для всей туманности. Вообще говоря, она зависит от температуры центральной звезды и от оптической толщины туманности за границей серии Лаймана. Мы рассмотрим два крайних случая: 1) туманность поглощает небольшую часть излучения звезды (τ1 << 1) и 2) туманность поглощает всю энергию звезды за границей серии Лаймана (τ1 >> 1).
В первом случае можно считать, что е определяется лишь ионизирующим излучением, идущим непосредственно от звезды. Поэтому, полагая
есть энергия, получаемая электроном при фотоионизации, средняя для всей туманности. Вообще говоря, она зависит от температуры центральной звезды и от оптической толщины туманности за границей серии Лаймана. Мы рассмотрим два крайних случая: 1) туманность поглощает небольшую часть излучения звезды (τ1 << 1) и 2) туманность поглощает всю энергию звезды за границей серии Лаймана (τ1 >> 1).
В первом случае можно считать, что е определяется лишь ионизирующим излучением, идущим непосредственно от звезды. Поэтому, полагая
|
|
(40) |
где k - постоянная Больцмана, мы для величины A получаем
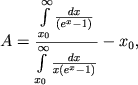
|
(41) |
Во втором случае фотоионизация происходит как благодаря излучению, идущему от звезды, так и благодаря диффузному излучению самой туманности. При больших τ1 можно, однако, считать, что все кванты, испускаемые при захватах электронов на первый уровень, поглощаются в самой туманности, т. е. что число ионизации, происходящих под влиянием диффузного излучения, равно ![]() , а энергия, которую электроны получают при этом, равна
, а энергия, которую электроны получают при этом, равна ![]() . Поэтому и в данном случае диффузного излучения туманности можно не учитывать. Надо только Ci и Cisi суммировать, не от 1, а от 2. Для А мы теперь находим
. Поэтому и в данном случае диффузного излучения туманности можно не учитывать. Надо только Ci и Cisi суммировать, не от 1, а от 2. Для А мы теперь находим
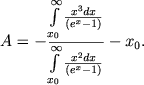
|
(42) |
Значения величины А, вычисленные по формулам (41) и (42), приведены в табл. XI.
Таблица XI
| T∗/1000 | I | II | ||
| A | AT∗/1000 | A | AT∗/1000 | |
| 20 | 0,90 | 18 | 1,24 | 25 |
| 40 | 0,83 | 33 | 1,46 | 58 |
| 60 | 0,77 | 46 | 1,63 | 98 |
| 80 | 0,71 | 57 | 1,76 | 141 |
В дополнение к равенству (6) положим:
|
|
(43) |
|
|
(44) |
|
|
(45) |
Тогда вместо (37) получаем
|
|
(46) |
Это есть окончательный вид соотношения, связывающего температуру ядра с электронной температурой туманности. Чтобы применить это соотношение к конкретным туманностям, надо еще вычислить коэффициенты В, С и D, а также дать формулы для нахождения средней степени ионизации в туманности.
Для вычисления коэффициентов В, С и D мы имеем следующие формулы. Согласно Cillie (см. статью, цитированную в главе I), энергия, излучаемая 1 см3 за 1 сек. при free-free transitions, равна
|
|
(47) |
а энергия, излучаемая при захвате на i-й уровень, равна
|
|
(48) |
При наших обозначениях первое из этих выражений есть nen+ƒ , а второе - nen+Ci(εi+hνic).
Согластно Shotaro Mlyamoto [9], для величины Di имеем
|
|
(49) |
где ![]() - среднее эффективное сечение для возбуждения i-гo состояния от нормального. Можно принять, что значения
- среднее эффективное сечение для возбуждения i-гo состояния от нормального. Можно принять, что значения ![]() даются таблицей:
даются таблицей:
| i | 2 | 3 | 4 | 5 |
| 1,0 | 0,2 | 0,1 | 0,06 |
если выражать ![]() в единицах a02π = 0,88 ⋅ 10-16 см2. Величина Dc определяется формулой, аналогичной (49), причем в этом случае
в единицах a02π = 0,88 ⋅ 10-16 см2. Величина Dc определяется формулой, аналогичной (49), причем в этом случае ![]() = 0,2 и вместо hν1c стоит энергия ионизации hν1i.
= 0,2 и вместо hν1c стоит энергия ионизации hν1i.
Значения коэффициентов В, С и D, вычисленные с помощью вышеуказанных формул, приведены в табл. XII.
Таблица XII
| Te/1000 | B | BTe/1000 | C/1000 | D/1000 |
| 5 | 1,02 | 5 | 12 | 0,001 |
| 7,5 | 1,04 | 8 | 12 | 3,0 |
| 10 | 1,06 | 11 | 12 | 250 |
| 12,5 | 1,08 | 14 | 12 | 2500 |
| 15 | 1,10 | 17 | 12 | 16000 |
Из табл. XII, между прочим, видно, что коэффициент D меняется с электронной температурой очень быстро. Это значит, что величину ![]() , входящую в соотношение (46), достаточно знать лишь приближенно. Мы можем указать, например, следующий способ для нахождения этой величины.
, входящую в соотношение (46), достаточно знать лишь приближенно. Мы можем указать, например, следующий способ для нахождения этой величины.
Принимая, что степень ионизации в туманности меняется согласно закону (11), мы получаем
|
|
(50) |
где ![]() есть степень ионизации, определяемая обычной ионизационной формулой [т.е. формулой (11) при τ=0]. Для нахождения величины
есть степень ионизации, определяемая обычной ионизационной формулой [т.е. формулой (11) при τ=0]. Для нахождения величины ![]() надо знать коэффициент делюции и электронную плотность при τ=0. Используя хорошо известные формулы
надо знать коэффициент делюции и электронную плотность при τ=0. Используя хорошо известные формулы
|
|
(51) |
|
|
(52) |
|
|
(53) |
где m∗ - фотографическая величина ядра и D" - угловой диаметр туманности в секундах дуги. Другая интересующая нac величина - число свободных электронов в 1 см3 при τ=0 - может быть найдена из формулы
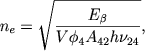
|
(54) |
где Eβ - энергия, излучаемая туманностью в линии Hβ. Принимая, что на долю линии Hβ приходится 1/15 часть полной анергии, излучаемой туманностью в видимой части спектра, и что толщина туманности равна 1/10 части ее радиуса, вместо (54)) получаем
|
|
(55) |
где mn - видимая величина туманности и r - расстояние до туманности в парсеках. Таким образом среднюю степень ионизации в туманности можно определить из формул (50), (11) (при τ=0), (53) и (55).
Соотношение (46) может быть использовано для нахождения электронной температуры туманности, если температура ядра уже найдена. Как известно, методы для определения температур ядер впервые были разработаны Zanstra [10]. Один из этих методов (метод "небулия") основан на предположении, что вся энергия, получаемая свободными электронами при фотоиониэации, идет на возбуждение линий "небулия". При пользовании этим методом температура ядра определяется из соотношения
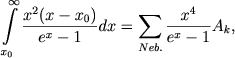
|
(56) |
в котором величины Ak (полученные из наблюдений) равны
|
|
(57) |
где Ek - полная энергия, излучаемая туманностью в данной линии, а Eν∗ - энергия, излучаемая ядром в единичном интервале частот в том же месте спектра. В действительности на возбуждение линий "небулия" расходуется только доля энергии свободных электронов. Согласно соотношению (46), эта доля равна ![]() . Поэтому вместо (56) мы получаем следующее, более точное соотношение для определения температуры ядра
. Поэтому вместо (56) мы получаем следующее, более точное соотношение для определения температуры ядра
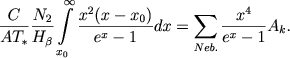
|
(58) |
Таким образом температуру туманности и температуру ядра следует находить путем совместного решения уравнений (46) и (58).
Выведенные уравнения мы применили к некоторым из планетарных туманностей. Результаты вычислений приведены в табл. XIII. В первом столбце дается номер туманности по каталогу NGC или JC, во втором столбце - отношение
![]() , по сводке Berman [11], в третьем - температура ядра, определенная методом "небулия", по данным Zanstra [10], Berman [12] и Page [13], в четвертом - исправленная температура ядра, в пятом - электронная температура туманности,
, по сводке Berman [11], в третьем - температура ядра, определенная методом "небулия", по данным Zanstra [10], Berman [12] и Page [13], в четвертом - исправленная температура ядра, в пятом - электронная температура туманности,
Таблица XIII
| Объект | T∗/1000 | Te/1000 | Излучение в непрерывном спектре | Возбуждение N1 и N2 | Столкновения с атомами водорода |
W | |||
| метод "небулия" |
испра- вленная |
||||||||
| NGC 7672 | 3,7 | 599 | 76 | 14 | 10 | 30 | 60 | 0,01 | 3 ⋅ 10-15 |
| NGC 7009 | 3,1 | 40 | 45 | 10 | 15 | 55 | 30 | 0,04 | 3 ⋅ 10-15 |
| NGC 6572 | 2,4 | 40 | 48 | 13 | 15 | 40 | 45 | 0,005 | 4 ⋅ 10-14 |
| NGC 6826 | 2,0 | 27 | 29 | 9 | 25 | 60 | 15 | 0,04 | 2 ⋅ 10-14 |
| JCII 4593 | 1,7 | 24 | 25 | 10 | 30 | 60 | 10 | 0,01 | 2 ⋅ 10-13 |
| NGC 6543 | 1,6 | 33 | 41 | 11 | 20 | 30 | 50 | 0,02 | 1 ⋅ 10-14 |
в шестом, седьмом и восьмом - доля энергии свободных электронов, расходуемая соответственно при захватах и free-free transitions, при столкновениях с атомами OIII и при столкновениях с атомами водорода, в девятом - величина ![]() и, наконец, в десятом - коэффициент дилюции.
и, наконец, в десятом - коэффициент дилюции.
Из рассмотрения табл. XIII можно сделать следующие выводы:
- Предположение Zanstra о переходе всей энергии свободных электронов в излучение линий "небулия" является весьма грубым. Таким путем электроны теряют лишь околополовины своей энергии. Соответственно этому температуры ядер, определенные методом "небулия", должны быть повышены на несколько тысяч или даже десятков тысяч градусов.
- Электронные температуры планетарных туманностей заключены в интервале 9000 - 14000°; . Строго говоря, эти значения являются верхней границей температур туманностей, так как электроны могут терять энергию еще другими, не учтенными нами способами. Для сравнения приведем электронные температуры туманностей, полученные другим методом, а именно - по отношению интенсивностей линий λ 4959 (N2) и λ 4363. Этот метод, впервые указанный В. А. Амбарцумяном [14], был применен к туманностям Miyamoto [9] и Menzel [15]. Первый автор получил температуры в интервале 10000 - 25000°; , а второй - в интервале 6000 - 10000°; . Расхождение между этими результатами обусловлено трудностью вычисления вероятностей неупругих столкновений электронов с атомами OIII.
Естественно думать, что электронные температуры совпадают с температурами протонов и нейтральных атомов водорода. Однако для туманностей, расширяющихся с градиентом скорости, Zanstra [8] указал одну причину, которая, по его мнению, ведет к крайне низким скоростям водородных атомов. Эта причина - торможение быстро летящих атомов при поглощении Lα-квантов. Zanstra произвел приближенный подсчет и получил, что каждый атом за время своей нейтральной жизни должен потерять почти всю свою кинетическую энергию. Однако, как уже указывалось, Zanstra получил неверное значение для плотности Lα-излучения. Кроме того, он не учитывал излучения, идущего от самих быстро летящих атомов. Поэтому вывод Zanstra является ошибочным. Более точные подсчеты (приводить которые мы здесь не будем) доказывают, что практически температуры электронов, протонов и нейтральных атомов водорода между собою совпадают. Поэтому электронные температуры, найденные нами в этом параграфе, являются температурами туманностей в целом.
Отметим еще один результат, вытекающий из соотношения (37). Как известно, наблюденный бальмеровский декремент несколько более крут, чем теоретический (вычисленный Cillie). Значительную часть этого расхождения Berman [11] удалось объяснить явлением пространственного покраснения. Все же в некоторых случаях расхождение осталось, и, вследствие этого, Miyamoto [9] выдвинул гипотезу о влиянии столкновений на бальмеровский декремент. Мы сейчас покажем, что это влияние незначительно.
Найдем отношение числа переходов с первого уровня на k-й под влиянием столкновения к числу захватов на k-й. уровень. Для всей туманности это отношение, очевидно, равно ![]() . Используя соотношение (37), мы можем написать следующую цепь неравенств:
. Используя соотношение (37), мы можем написать следующую цепь неравенств:
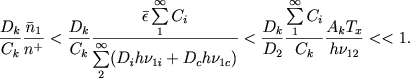
|
(59) |
Эти неравенства действительно устанавливают, что столкновения свободных электронов с водородными атомами не могут заметно изменить бальмеровский декремент, даваемый рекомбинацнонной теорией (точнее говоря, энергия, получаемая электронами при фотоионизации, недостаточна для этого). На самом деле небольшие расхождения между теорией и наблюдениями объясняются, невидимому, неравномерностью пространственного покраснения.
В заключение остановимся на методах для определения температур ядер туманностей. Кроме метода "небулия", о котором речь шла выше, Zanstra разработал еще бдин метод, для определения температур ядер, который для краткости мы назовем методом водорода. В основе этого метода лежит единственное предположение, что туманность поглощает все излучение, идущее от звезды за границей серии Лаймана. Так как из каждого Lα-кванта, поглощенного в туманности, возникает один и только один бальмеровский квант, то это предположение приводит к следующему соотношению для определения температуры ядра:
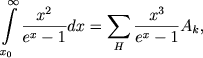
|
(60) |
где суммирование распространено на всю бальмеровскую серию (включая континуум).
Комбинируя соотношения (56) и (60), Stoy [16] получил новый метод для определения температур ядер - по отношению интенсивностей линий "небулия" и бальмеровской серии водорода. Применение этого метода к туманностям и новым Звездам (Stoy [16], Page [13], Oehler 18) привело к значительно более низким температурам, чем полученные методам Zanstra. Пользуясь вышеприведенными формулами, мы можем сейчас высказать следующие соображения о всех перечисленных методах для определения температур ядер туманностей.
-
При практическом применении метода водорода большие трудности возникают при определении величин Ak для линии Нα и для бальмеровекого континуума. Однако трудности легко обойти, если учесть результаты работы Cillie. Так как отношение числа квантов, излучаемых туманностями в линии Нβ, к общему числу бальмеровских квантов равно
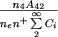 , то вместо соотношения (60) мы получаем
, то вместо соотношения (60) мы получаем
где величины Aβ и х в правой части относятся к линии Нβ. Для определения температуры ядра из этого соотношения точного значения Te не требуется, так как величина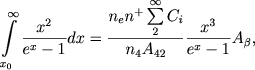
(61) 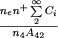 почти не меняется с Te (можно принять, что эта величина равно 9,2).
почти не меняется с Te (можно принять, что эта величина равно 9,2).
- Метод "небулия", основанный на допущении, что вся энергия свободных электронов переходит в излучение линий "небулия", дает, очевидно, нижнюю границу температуры ядра. Как было выяснено, после уточнения этого метода, температура ядра должна определяться из соотношения (58). Но подставляя в это соотношение значения А и С из формул (42) и (44), мы видим, что оно превращается в соотношение (61). Это означает, что уточненный метод "небулия" эквивалентен методу водорода. Физически такой результат вполне понятен, ибо оба метода Zanstra основаны на сравнении одних и тех же участков непрерывного спектра звезды (видимого и за границей серии Лаймана).
-
Если в правой части соотношения (46) пренебречь первым и третьим членами, то мы придем к уравнению
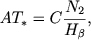
(62) которое соответствует методу Stoy. Вполне понятно, что при определении температур ядер из уравнения (62) должны получаться весьма низкие значения.
Таким образом мы приходим к следующему выводу: температуры ядер туманностей должны определяться методом водорода, т. е. из уравнений (60)) или (61); после этого температуры самих туманностей могут быть найдены из уравнения (46).
Можно, однако, указать другую точку зрения. Если температуры туманностей, определенные Menzel по отношению интенсивностей линий λ 4959 и λ 4363, правильны, то в соотношении (46) последний член оказывается малым, и это соотношение принимает вид
|
|
(63) |
Однако температуры ядер, определенные из уравнения (63), будут значительно ниже температур, определенных из уравнения (60). Это противоречие можно устранить, если сделать предположение, что распределение энергии в спектре ядра сильно отличается от распределения Планка. В таком случае уравнение (60) дает цветовую температуру, характеризующую отношение интенсивностей в видимой части спектра звезды и за границей серии Лаймана, а уравнение (63) - температуру, характеризующую распределение энергии за границей серии Лаймана. Соотношение (46) дает в этом случае верхнюю границу температуры туманности.
<< 3.2 Поле Lα-излучения | Оглавление | Глава IV. Оболочки новых звезд >>
|
Публикации с ключевыми словами:
оболочки звезд - перенос излучения
Публикации со словами: оболочки звезд - перенос излучения | |
|
См. также:
| |