Астронет > Движущиеся оболочки звезд

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Движущиеся оболочки звезд << 2.1 Нижняя граница атмосферы | Оглавление | 2.3 Контуры спектральных линий >>

2.2 Изменение возбуждения вдоль радиуса

Как было выяснено в предыдущей главе, степень возбуждения атомов в движущейся атмосфере зависит от двух параметров: от температуры звезды T_∗ и от параметра х. Для параметра х мы имеем

$x=\frac{1}{2un_1 x_{12} W} \frac{\overline{dv}}{ds},$ (15)

где u - средняя термическая скорость атомов, x₁₂ - средний коэффициент поглощения в спектральной линии, рассчитанный на один атом, и $\frac{\overline{dv}}{ds}$ - усредненный по направлениям градиент скорости. Чтобы найти, как меняется степень возбуждения вдоль радиуса, нам надо представить параметр x в виде функции от r.

Легко видеть, что в атмосфере, образованной выбрасываемой из звезды материей, градиент скорости равен

$\frac{dv}{ds} = \frac{dv}{dr} \cos^2\theta+\frac{v}{r}\sin^2\theta,$ (16)

где $\frac{dv}{dr}$ - градиент скорости вдоль радиуса и θ - угол между данными направлениями и радиусом-вектором. Если скорость истечения постоянная. то

$\frac{\overline{dv}}{ds} = \frac{2}{3} \frac{v}{r}.$ (17)

Уситывая (17), (5) и (2), вместо (15) находим

$x = x_0 \left(\frac{r}{r_0}\right)^3,$ (18)

где

$x_0 = \frac{v f(T_*)}{3ux_{12} r_0 {n_e^0}^2} .$ (19)

Так как n_e⁰r₀ = 0,5 ⋅ 10²⁴, а для линии L_α и x₁₂ = 6,8 ⋅ 10^-8, то для водорода

$x_0 = 10^{-17} \frac{vf(T_*)}{n_e^0} .$ (20)

При v = 100 км/сек, для двух рассмотренных выше случаев (T=20000°; и T=50000°; ) это дает х₀=0,001 и х₀=0,1.

Мы видим, что в случае истечения материи с постоянной скоростью параметр х возрастает пропорционально кубу радиуса. Следовательно, в этом случае степень возбуждения весьма быстро убывает с увеличением радиуса. Чтобы представить степень возбуждения в виде функции от r, надо вычислить х по формуле (18) и затем воспользоваться таблицами 2 и 3 предыдущей главы. Заметим, что такое представление будет верным только во внутренних частях атмосферы. Во внешних же частях атмосферы, где атмосфера прозрачна для излучения в линиях субординатных серий, величины $\frac{n_i}{n_1}$ будут просто пропорциональны $\frac{n_i n^+}{n_1}$ т.е. степень возбуждения будет убывать как $\frac{1}{r^2}$ .

Представляет интерес нахождение границы между непрозрачной и прозрачной частями атмосферы, т.е., иначе говоря, верхней границы обращающего слоя. Так как эта граница различна для разных линий, то для определенности мы найдем ее для линии Н_α, определяя ее соотношением

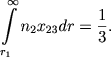
$\int\limits_{r_{1}}^{\infty} n_2 x_{23} dr = \frac{1}{3} .$ (21)

Для больших значений x мы приближенно имеем

$\frac{n_2}{n_1} = (1-p) \frac{B_{1c} \rho_{1c}^*}{xA_{21}} ,$ (22)

[см. формулу (25) предыдущей главы] и, используя (5), (18) и (21), получаем

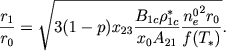
$\frac{r_1}{r_0} = \sqrt{3(1-p) x_{23} \frac{B_{1c} \rho_{1c}^*}{x_0 A_{21}} \frac{{n_e^0}^2 r_0}{f(T_*)}} .$ (23)

Для двух случаев, рассмотренных выше, формула (23) дает $\frac{r_1}{r_0}=12$ и $\frac{r_1}{r_0}=4$ . Таким образом мы видим, что рассматриваемые звезды обладают весьма протяженным обращающим слоем. Этот вывод, между прочим, должен иметь значение при вычислении контуров линий поглощения, образованных атмосферами этих звезд.

С вопросом об изменении степени возбуждения вдоль радиуса тесно связан вопрос о количестве энергии, излучаемой разными слоями атмосферы. Если степень возбуждения как функция от радиуса известна, то этот вопрос решается с помощью формул (8) и (9) (в которых, однако, интегрировать надо не по всему объему атмосферы, а только по интересующему слою). При такого рода вычислениях выясняются следующие важные обстоятельства:

Пусть H_k⁰ и H_k^' суть количества энергии, излучаемой в k-й линии бальмеровской серии соответственно обращающим слоем и прозрачной частью атмосферы. Мы, очевидно, имеем

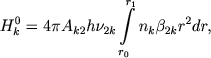
$H_k^0 = 4\pi A_{k2} h\nu_{2k} \int\limits_{r_0}^{r_1} n_k \beta_{2k} r^2 dr ,$ (24)

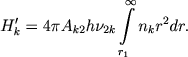
$H_k^{\prime} = 4\pi A_{k2} h\nu_{2k} \int\limits_{r_1}^{\infty} n_k r^2 dr .$ (25)

Вычисление этих интегралов показывает, что основную часть энергии излучает не прозрачная часть атмосферы, а обращающий слой. Так, например, в первом из наших случаев (T=20000°;) доля энергии, излучаемой прозрачной частью атмосферы, составляет только около 20%. Этот вывод противоречит общепринятому мнению и доказывает правильность нашей точки зрения.
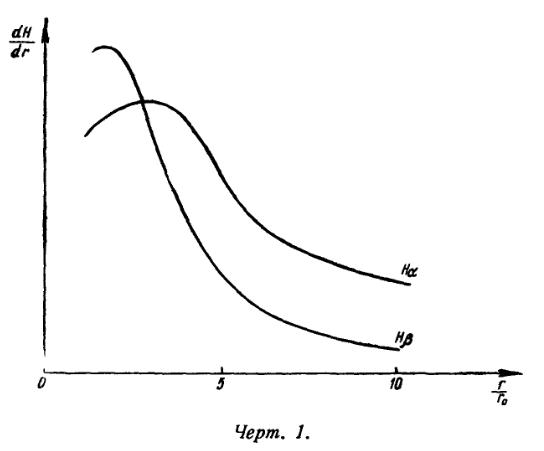
Пусть 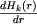$\frac{dH_k(r)}{dr}$ есть количество энергии, излучаемой в k-й бальмеровской линии сферическим слоем единичной толщины, находящимся на расстоянии r от центра звезды. Вычисления показывают, что для разных линий эта величина достигает максимума в разных местах. Для примера мы вычислили эту величину для линий H_α и H_β (при Т=20000°; ). Результаты вычислений в условных единицах представлены на черт. 1.
Из чертежа видно, что основная часть энергии в линии H_β излучается более глубокими слоями, чем в линии H_α. Например, половина энергии в линии H_β излучается внутри сферы радиуса r = 3r₀, а половина энергии в линии H_α - внутри сферы радиуса r = 6r₀. Этот вывод важен для объяснения отмеченной наблюдателями стратификации водородного излучения в протяженных атмосферах (см., например, статью

Goedicke о звезде W Cephei [3] и статью Baldwin о звезде γ Cassiopeiae [4]).
В заключение заметим, что, хотя изложенные выше результаты получены для вполне определенной модели атмосферы (скорость истечения материи постоянна, плотность убывает обратно пропорционально квадрату радиуса), однако, несомненно, что в общих чертах они справедливы для всех горячих сверхгигантов. Чтобы проделать подобное исследование для конкретной звезды, необходимо знать распределение плотностей и скоростей в ее атмосфере. Важный вопрос о том, как получить эти данные из наблюдений, может быть решен путем сравнения наблюденных и теоретических контуров спектральных линий. Проблеме теоретического определения контуров линий, образованных движущимися атмосферами, посвящается следующий параграф.

<< 2.1 Нижняя граница атмосферы | Оглавление | 2.3 Контуры спектральных линий >>

Публикации с ключевыми словами: оболочки звезд - перенос излучения Публикации со словами: оболочки звезд - перенос излучения
См. также: Сбрасывающая массивную оболочку звезда G79.29+0.46 Обнаружение горячего водяного пара в оболочке углеродной звезды. Оболочки в туманности Яйцо Освещённость Планетарные туманности

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце