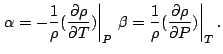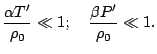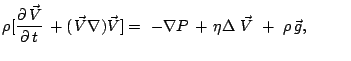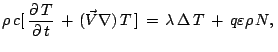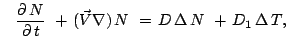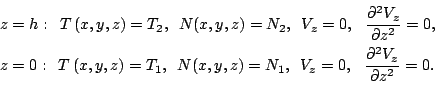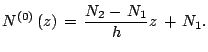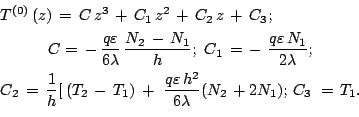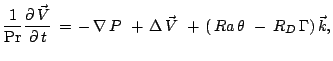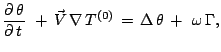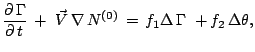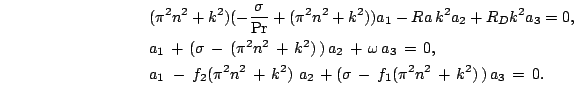<< 2. Уравнения конвекции | Оглавление | 4. Моделирование развитой конвекции >>
3. Условия возникновения конвекции в мантии
Возникает вопрос: а при каких условиях в системе, поведение которой контролируется
гравитационным полем и внутренними источниками энергии, как это
явно следует из (3)-(6), возможно стационарное
механическое равновесие? Если мы будем рассматривать сферический
слой, мощность которого ![]() много меньше радиуса Земли,
много меньше радиуса Земли, ![]() , т. е.
при
, т. е.
при ![]() , сферичностью можно пренебречь и слой рассматривать
как плоский. Совместим координатную плоскость декартовой системы
координат с нижней границей слоя. Ось
, сферичностью можно пренебречь и слой рассматривать
как плоский. Совместим координатную плоскость декартовой системы
координат с нижней границей слоя. Ось ![]() направим вдоль вектора
направим вдоль вектора
![]() .
.
Для того чтобы в явном виде выписать (3)-(6) как
систему, нам необходимо использовать уравнение состояния
![]() . Поскольку даже состав внутренних оболочек оценен
достаточно грубо, то для слоя мантии в качестве уравнения
состояния можно использовать приближение
. Поскольку даже состав внутренних оболочек оценен
достаточно грубо, то для слоя мантии в качестве уравнения
состояния можно использовать приближение
Следовательно, предполагается, что мощность слоя достаточно мала для того, чтобы можно было принять, что распределения температуры, давления и плотности хорошо описываются их средними значениями, которые мы обозначим
Тогда в стационарном состоянии механического равновесия (3)-(4) дают
Уравнение (9) называют условием распределения гидростатического давления в жидкости. Взяв
т. е. в однородном гравитационном поле гидростатически распределенная плотность может изменяться только вдоль вектора
Вопрос заключается в том, является ли это состояние устойчивым или произвольные,
даже малые возмущения могут вывести систему из механического равновесия. Мы имеем
дело с исследованием проблемы устойчивости системы. Состояние системы,
характеризующееся набором термодинамических параметров ![]() , называют
устойчивым по Ляпунову [7], если для любого
, называют
устойчивым по Ляпунову [7], если для любого
![]() существует
существует
![]() такое, что
такое, что
здесь
Для упрощения задачи примем широко используемое в геодинамике приближение
Буссинеска, [8], в котором изменение плотности учитывается только в
уравнении баланса импульса (3), а в остальных уравнениях системы ![]() принимается постоянной. Тогда из уравнения (6) следует
принимается постоянной. Тогда из уравнения (6) следует
![]() (приближение несжимаемой жидкости), и в уравнении (3) третий член
в правой части обращается в нуль. После стандартных преобразований [4, 8]
уравнение для баланса энтропии при дополнительном
условии
(приближение несжимаемой жидкости), и в уравнении (3) третий член
в правой части обращается в нуль. После стандартных преобразований [4, 8]
уравнение для баланса энтропии при дополнительном
условии
существенно упростится и можно записать
При этом уравнение состояния используется в виде
где в выражениях (14)-(18)
Применяя оператор
Условия в (22) на вертикальную компоненту скорости означают, что границы не проницаемые для жидкости и так называемые «скользкие» (последнее принято из соображений удобств последующих вычислений). Решение задачи (21)-(22) имеет вид
Подставляя (23) в (20), получим
Для характерных значений параметров в мантии
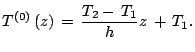
Тогда краевая задача для возмущений в линейном относительно малых возмущений приближении может быть приведена к виду
где
(14)-(17) не содержат нелинейных относительно возмущений членов, поскольку вошли только градиенты гидростатически равновесных распределений температуры и концентраций. Тогда входящие в (25)-(28) функции вида
С тем чтобы избавиться от члена с градиентом давления в (25)
(для возмущения давления весьма сложно сформулировать граничные
условия), используется стандартный прием. Возьмем
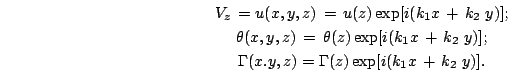 от
обеих частей уравнения и спроектируем на ось
от
обеих частей уравнения и спроектируем на ось ![]() . При этом будем
учитывать, что ни коэффициенты в уравнениях
(25)-(28), ни граничные условия не зависят от
горизонтальных координат. Поэтому выражения для пространственных
амплитуд можно выбрать в виде
. При этом будем
учитывать, что ни коэффициенты в уравнениях
(25)-(28), ни граничные условия не зависят от
горизонтальных координат. Поэтому выражения для пространственных
амплитуд можно выбрать в виде
где верхний индекс в скобках означает порядок производной по
Подставляя (30) в (25)-(27) с учетом(29), получим
Из условий существования нетривиального решения системы однородных уравнений (30) получаем
Представив декремент затухания в виде:
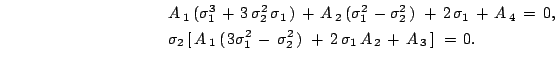 и разделяя действительную и мнимую части,
получим
и разделяя действительную и мнимую части,
получим
Таким образом, в системе возможны как монотонные, строго убывающие либо возрастающие, так и колебательные возмущения.
Особый интерес представляет состояние нейтральной устойчивости, т. е.
![]() ,
,
![]() при
при ![]() . Это граница между устойчивым и
неустойчивым состоянием. Как следует из (33), оно
достигается при
. Это граница между устойчивым и
неустойчивым состоянием. Как следует из (33), оно
достигается при 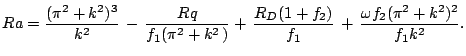 , откуда
, откуда
Для характерных условий в мантии параметр
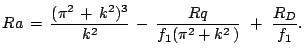 весьма мал и
(34) можно оставить в виде
весьма мал и
(34) можно оставить в виде
Из (35) видно, что устойчивость системы различна для возмущений различной длины волны,
Принципиальное значение имеет вклад второго члена, отражающего действие внутренних
источников тепла (
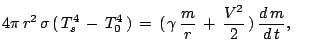 ). Их наличие приводит
к уменьшению плотности этого компонента смеси даже в том случае,
когда источники тепла связаны с более плотным компонентом смеси.
Отсюда следует парадокс устойчивости, впервые описанный в
[9, 10]. Он состоит в том, что при достаточной мощности
внутренних источников тепла, концентрация которых определяется
содержанием более плотного компонента смеси, имеется область
значений параметров, когда система остается в устойчивом
гидростатическом состоянии при увеличении концентрации тяжелого
компонента по направлению к верхней холодной границе плоского
слоя.
). Их наличие приводит
к уменьшению плотности этого компонента смеси даже в том случае,
когда источники тепла связаны с более плотным компонентом смеси.
Отсюда следует парадокс устойчивости, впервые описанный в
[9, 10]. Он состоит в том, что при достаточной мощности
внутренних источников тепла, концентрация которых определяется
содержанием более плотного компонента смеси, имеется область
значений параметров, когда система остается в устойчивом
гидростатическом состоянии при увеличении концентрации тяжелого
компонента по направлению к верхней холодной границе плоского
слоя.
Численное моделирование развитой конвекции показало, что система стремится вынести внутренние источники тепла, входящие в один из компонентов смеси к верхней холодной границе слоя [11].
<< 2. Уравнения конвекции | Оглавление | 4. Моделирование развитой конвекции >>
|
Публикации с ключевыми словами:
геофизика - строение Земли - конвекция
Публикации со словами: геофизика - строение Земли - конвекция | |
См. также:
Все публикации на ту же тему >> | |