<< Титульный лист
| Оглавление |
2. Уравнения конвекции >>
Представления о медленных, конвективных, движениях во внутренних оболочках
играют определяющую роль при изучении динамики планеты. Как это обычно бывает с
ключевыми проблемами, она оказалась комплексной, зависящей от многочисленных
физических и математических аспектов. Здесь мы в большей мере коснемся
математических вопросов, тогда как геофизическая сторона проблемы будет
затронута только по мере необходимости, что восполняется многочисленными обзорами
[1]-[3].
Итак, при внешнем воздействии в сплошной среде возникают внутренние напряжения,
вызывающие ее деформацию. Математически напряжения описываются в
каждой точке среды компонентами тензора напряжений,
 , а деформации также тензором 2-го ранга, тензором
деформаций,
, а деформации также тензором 2-го ранга, тензором
деформаций,  . При малых деформациях этот тензор линеен
относительно своих компонент. Диагональные компоненты имеют смысл
относительных удлинений вдоль главных осей тензора,
а недиагональные - углов поворота [4]. Вид зависимости
компонент тензора деформаций от тензора напряжений определяет
реологические свойства вещества. Среди разнообразных реализаций
этой зависимости особую роль играют два предельных варианта. При
линейной зависимости между компонентами тензора деформаций и
тензора напряжений выполняется закон Гука. Для изотропных сред его
можно записать в виде [4]
. При малых деформациях этот тензор линеен
относительно своих компонент. Диагональные компоненты имеют смысл
относительных удлинений вдоль главных осей тензора,
а недиагональные - углов поворота [4]. Вид зависимости
компонент тензора деформаций от тензора напряжений определяет
реологические свойства вещества. Среди разнообразных реализаций
этой зависимости особую роль играют два предельных варианта. При
линейной зависимости между компонентами тензора деформаций и
тензора напряжений выполняется закон Гука. Для изотропных сред его
можно записать в виде [4]
 |
(1) |
где

и
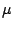
- соответственно модули всестороннего сжатия и
сдвига. Другой вариант предельной зависимости - приближение
вязкой жидкости:
 |
(2) |
По-видимому, именно анализ геофизических наблюдений позволил
установить, что реалогические свойства вещества зависят не только
от

-условий, но и от скорости изменения внешнего воздействия.
Так, относительно короткопериодных (периоды от долей секунды до
нескольких часов) возмущений, возникающих при землетрясениях или
взрывах, верхняя оболочка Земли проявляет свойства упругого
твердого тела (рис. 1 из [
5]) в котором сложное возмущение
распалось на два типа - волны сжатия,

, и волны сдвига

. При этом на каждой неоднородности возникают обменные
преломленные и отраженные волны. С другой стороны, в ответ на
медленно изменяющиеся воздействия, обусловленные снятием ледовой
нагрузки последнего оледенения под большими регионами, такими как
Фенноскандия, вещество проявляет линейную связь между напряжениями
и скоростью деформации, типа (
2), характерную для вязкой
жидкости [
3].
|
|
Рис. 1.
Скоростной разрез Земли, из [5] |
Поэтому понятно, что из сейсмических наблюдений мы не можем получить информацию о
глубине мантии, охваченной медленным вязким течением. Нужны дополнительные
наблюдения. Они получены из сопоставления состава вещества земной коры и мантии.
Результаты исследования состава мантийных образцов, выводимых на поверхность по
трубкам взрыва (кимберлитовые трубки), часть из которых является алмазоносными,
показало высокую выдержанность состава мантийного резервуара. И этот состав
соответствует составу одного из классов каменных метеоритов - углистых хондритов.
Но земная кора (оболочка, расположенная выше поверхности Мохоровичича, рис. 1)
резко обогащена относительно мантии такими элементами, как Fe, Al, Mg, Mn, а
содержание редкоземельных элементов и U, Th на два порядка превышает мантийное.
Многочисленные тонкие оценки, огромный вклад в которые внесен отечественной школой
акад. А. П. Виноградова [
6], показали, что для обеспечения такого состава коры
необходимо транспортировать к поверхности названные элементы из слоя мантии не
менее 1000 км. Имеется два физических механизма переноса не ионизированного
вещества в сплошной среде: диффузия и конвективный массоперенос. За время 4.6 млрд лет
(возраст Земли) диффузия при

- условиях коры может проработать 10
километровый слой пород. Для переработки 1000 км слоя потребуется в 10000 раз
большее время. Следовательно, такую транспортировку мог обеспечить только
конвективный массоперенос. Другим важнейшим аргументом в пользу наличия
конвективных течений в мантии является комплекс наблюдений, приведший к заключению
о перемещении литосферных плит относительно друг друга и нижележащей мантии [2, 3].
Здесь мы остановимся на особенностях конвекции в мантии и не будем затрагивать
проблемы магнитной гидродинамики ядра.
<< Титульный лист
| Оглавление |
2. Уравнения конвекции >>
![]() , а деформации также тензором 2-го ранга, тензором
деформаций,
, а деформации также тензором 2-го ранга, тензором
деформаций, ![]() . При малых деформациях этот тензор линеен
относительно своих компонент. Диагональные компоненты имеют смысл
относительных удлинений вдоль главных осей тензора,
а недиагональные - углов поворота [4]. Вид зависимости
компонент тензора деформаций от тензора напряжений определяет
реологические свойства вещества. Среди разнообразных реализаций
этой зависимости особую роль играют два предельных варианта. При
линейной зависимости между компонентами тензора деформаций и
тензора напряжений выполняется закон Гука. Для изотропных сред его
можно записать в виде [4]
. При малых деформациях этот тензор линеен
относительно своих компонент. Диагональные компоненты имеют смысл
относительных удлинений вдоль главных осей тензора,
а недиагональные - углов поворота [4]. Вид зависимости
компонент тензора деформаций от тензора напряжений определяет
реологические свойства вещества. Среди разнообразных реализаций
этой зависимости особую роль играют два предельных варианта. При
линейной зависимости между компонентами тензора деформаций и
тензора напряжений выполняется закон Гука. Для изотропных сред его
можно записать в виде [4]


