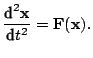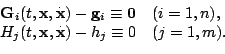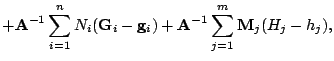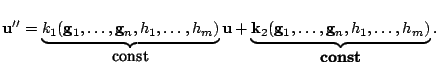<< 3. Методы теории специальных ... | Оглавление | 3.2. Сглаживающие преобразования >>
3.1. Линеаризация и регуляризация
Цель методов линеаризации и регуляризации состоит в том, чтобы представить уравнения движения в линейном и, самое главное, в регулярном виде.Рассмотрим сначала уравнения невозмущенного движения
Предположим, что уравнения (2) имеют интегралы
Условие независимости интегралов (3) не обязательно. Здесь
Далее введем временное и координатное преобразования:
которые позволяют перейти к новым переменным
Главная идея линеаризации и регуляризации состоит во введении в уравнения, записанные в новых переменных, интегральных соотношений (3). В результате уравнения принимают вид [1]
где штрих означает производную по
В возмущенном случае, применяя вышеизложенные преобразования, будем иметь слабонелинейные уравнения вида
Поскольку здесь интегральные параметры уже не являются постоянными и, кроме того, вследствие появления
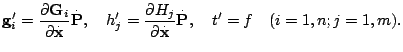
Таким образом, в результате подбора преобразований (4),
а также коэффициентов ![]() и
и
![]() можно получить
многочисленное семейство систем дифференциальных уравнений вида
(7). Среди таких систем широко используются на практике
системы уравнений в переменных Шперлинга-Боде [2]
и Кустаанхеймо-Штифеля [3]. В первой
можно получить
многочисленное семейство систем дифференциальных уравнений вида
(7). Среди таких систем широко используются на практике
системы уравнений в переменных Шперлинга-Боде [2]
и Кустаанхеймо-Штифеля [3]. В первой
<< 3. Методы теории специальных ... | Оглавление | 3.2. Сглаживающие преобразования >>
|
Публикации с ключевыми словами:
Небесная механика
Публикации со словами: Небесная механика | |
См. также:
Все публикации на ту же тему >> | |
Астрометрия
-
Астрономические инструменты
-
Астрономическое образование
-
Астрофизика
-
История астрономии
-
Космонавтика, исследование космоса
-
Любительская астрономия
-
Планеты и Солнечная система
-
Солнце