Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу << A.4 Элементы дифференциального и | Оглавление | A.6 Сферические функции >>

A.5 Криволинейные координаты

Если в области $ V$ трехмерного евклидова пространства заданы соотношения, ставящие в соответствие каждой точке $ (x,y,z)$ тройку чисел $ x^i,\ i=1,2,3$, причем

$\displaystyle x^1=f_1(x,y,z), \quad x^2=f_2(x,y,z), \quad x^3=f_3(x,y,z), $

то функции $ x^1, x^2, x^3$ называются криволинейными координатами точки.

Условие $ x^i=f_i(x,y,z)=\textrm{const},\ i=1,2,3$ определяет координатную поверхность. Две координатных поверхности, соответствующие различным координатам $ x^i, x^j, (i\neq j)$ пересекаются по координатной линии, соответствующей третьей координате $ x^k$.

Единичные векторы $ {\mathbf{i}}_1(x^1,x^2,x^3), {\mathbf{i}}_2(x^1,x^2,x^3), {\mathbf{i}}_3(x^1,x^2,x^3)$ касательные к координатным линиям $ x^1, x^2, x^3$ являются локальными базисными векторами.

В качестве локальных базисных векторов можно выбрать тройку векторов (не обязательно единичных), которые определяются уравнениями:

$\displaystyle {\mathbf{e}}_1(x^1,x^2,x^3)=\sqrt{g_{11}}\,{\mathbf{i}}_1, \quad {\mathbf{e}}_2(x^1,x^2,x^3)=\sqrt{g_{22}}\,{\mathbf{i}}_2, \quad {\mathbf{e}}_2(x^1,x^2,x^3)=\sqrt{g_{33}}\,{\mathbf{i}}_3, $

направленных по координатным линиям, где $ g_{ii}$ -- компоненты метрического тензора:

$\displaystyle g_{ik}(x^1,x^2,x^3)=\left.\Bigl(\frac{\partial{x}}{\partial{x}^i}\frac{\partial{x}}{\partial{x}^k} + \frac{\partial{y}}{\partial{x}^i}\frac{\partial{y}}{\partial{x}^k} + \frac{\partial{z}}{\partial{x}^i}\frac{\partial{z}}{\partial{x}^k}\Bigr)\right\vert _{(x^1,x^2,x^3)}. $

Локальные базисные векторы $ {\mathbf{e}}_1,{\mathbf{e}}_2, {\mathbf{e}}_3$ могут быть выражены через орты $ {\mathbf{i}},{\mathbf{j}}, {\mathbf{k}}$ декартовой системы координат по формулам:

$\displaystyle {\mathbf{e}}_i = \frac{\partial{x}}{\partial{x}^i}{\mathbf{i}} + \frac{\partial{y}}{\partial{x}^i}{\mathbf{j}} + \frac{\partial{z}}{\partial{x}^i}{\mathbf{k}}. $

Функции $ \frac{\partial{x}}{\partial{x}^i}, \frac{\partial{y}}{\partial{x}^i}, \frac{\partial{z}}{\partial{x}^i}$ являются направляющими косинусами орта $ {\mathbf{e}}_i$ по отношению к декартовым осям $ Ox, Oy, Oz$.

В качестве локальных базисных векторов можно выбрать тройку векторов $ {\mathbf{e}}^1, {\mathbf{e}}^2, {\mathbf{e}}^3$:

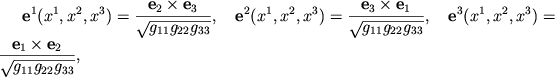
$\displaystyle {\mathbf{e}}^1(x^1,x^2,x^3)=\frac{{\mathbf{e}}_2\times {\mathbf{e}}_3} {\sqrt{g_{11}g_{22}g_{33}}}, \quad {\mathbf{e}}^2(x^1,x^2,x^3)=\frac{{\mathbf{e}}_3\times {\mathbf{e}}_1} {\sqrt{g_{11}g_{22}g_{33}}}, \quad {\mathbf{e}}^3(x^1,x^2,x^3)=\frac{{\mathbf{e}}_1\times {\mathbf{e}}_2} {\sqrt{g_{11}g_{22}g_{33}}}, $

направленных перпендикулярно к координатным поверхностям.

В базисе $ {\mathbf{e}}_1,{\mathbf{e}}_2, {\mathbf{e}}_3$ координаты вектора $ \mathbf{a}$ называются ковариантными координатами:

$\displaystyle a_i = a_i(x^1,x^2,x^3)={\mathbf{a}}\cdot{\mathbf{e}}_i,\ i=1,2,3, $

а в базисе $ {\mathbf{e}}^1, {\mathbf{e}}^2, {\mathbf{e}}^3$ -- контравариантными:

$\displaystyle a^i = a^i(x^1,x^2,x^3)={\mathbf{a}}\cdot{\mathbf{e}}^i,\ i=1,2,3. $

Справедливы формулы:

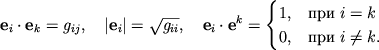
$\displaystyle {\mathbf{e}}_i\cdot {\mathbf{e}}_k=g_{ij}, \quad \vert{\mathbf{e}}_i\vert = \sqrt{g_{ii}}, \quad {\mathbf{e}}_i\cdot {\mathbf{e}}^k= \begin{cases} 1,& \textrm{при}\ i=k\\ 0,& \textrm{при}\ i\neq k. \end{cases}$

В частном случае прямоугольных декартовых координат $ x^1=x, x^2=y, x^3=z$ имеем:

$\displaystyle {\mathbf{e}}_1={\mathbf{e}}^1={\mathbf{i}}_1={\mathbf{i}}, \quad {\mathbf{e}}_2={\mathbf{e}}^2={\mathbf{i}}_2={\mathbf{j}}, \quad {\mathbf{e}}_3={\mathbf{e}}^3={\mathbf{i}}_3={\mathbf{k}}. $

Система криволинейных координат $ x^1, x^2, x^3$ является ортогональной, если

$\displaystyle g_{ik}(x^1,x^2,x^3)=0\ \textrm{при}\ i\neq k $

в каждой точке $ (x^1, x^2, x^3)$. Координатные линии, а значит, и векторы локального базиса $ {\mathbf{i}}_1, {\mathbf{i}}_2, {\mathbf{i}}_3$ будут перпендикулярны друг к другу в каждой точке.

Элемент объема $ dV$ в криволинейных координатах равен:

$\displaystyle dV = \sqrt{g}\,dx^1dx^2dx^3,\ \sqrt{g}= \sqrt{g_{11}g_{22}g_{33}}\,. $

Интеграл по объему от функции $ f(x,y,z)=f[x(x^1,x^2,x^3), y(x^1,x^2,x^3), z(x^1,x^2,x^3)]$ по ограниченной области $ V$ равен

$\displaystyle \int_V f(x,y,z)dV$ $\displaystyle = \iiint_V f(x,y,z)dx dy dz =$    
$\displaystyle =\iiint_V f[x(x^1,x^2,x^3), y(x^1,x^2,x^3), z(x^1,x^2,x^3)] \sqrt{g}dx^1dx^2dx^3.$    

Интеграл по объему не зависит от выбора системы координат и может быть выражен непосредственно через тройные интегралы по $ x,y,z$ или $ x^1, x^2, x^3$.

В сферических координатах $ \sqrt{g}=r^2\sin\theta$.


<< A.4 Элементы дифференциального и | Оглавление | A.6 Сферические функции >>

Публикации с ключевыми словами: астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени
См. также:
Все публикации на ту же тему >>

Мнения читателей [13]
Оценка: 3.5 [голосов: 304]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования