A.4 Элементы дифференциального и интегрального исчисления
Дифференциал функции ![]() в точке
в точке ![]() , если он существует,
равен:
, если он существует,
равен:
Дифференциал функции
![]() , если он
существует, равен:
, если он
существует, равен:
Если ![]() -- действительная функция, имеющая в интервале
-- действительная функция, имеющая в интервале
![]()
![]() -ую производную
-ую производную ![]() , то
, то
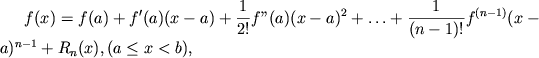
Градиентом скалярной функции
![]() называется
векторная функция, определяемая формулой:
называется
векторная функция, определяемая формулой:
Полный дифференциал ![]() скалярной функции
скалярной функции
![]() , соответствующий перемещению точки на
, соответствующий перемещению точки на
![]() равен:
равен:
Дифференциал
![]() радиус-вектора
радиус-вектора
![]() вдоль кривой
вдоль кривой
![]() , описываемой уравнением
, описываемой уравнением
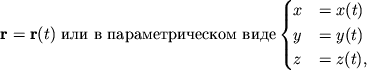
Квадрат элемента длины равен
Преобразование дифференциалов из сферической в декартову систему координат имеет вид:
<< A.3 Декартовы прямоугольные и | Оглавление | A.5 Криволинейные координаты >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |
Мнения читателей [13]
Астрометрия
-
Астрономические инструменты
-
Астрономическое образование
-
Астрофизика
-
История астрономии
-
Космонавтика, исследование космоса
-
Любительская астрономия
-
Планеты и Солнечная система
-
Солнце