A.3 Декартовы прямоугольные и сферические координаты вектора
Если базисные векторы или орты
![]() взаимно перпендикулярны и определяют оси системы координат
взаимно перпендикулярны и определяют оси системы координат
![]() , то разложение
, то разложение
Базисными векторами сферической системы координат является тройка
единичных векторов
![]() , направленных в сторону увеличения соответствующих
координат:
, направленных в сторону увеличения соответствующих
координат: ![]() -- расстояния,
-- расстояния, ![]() -- кошироты,
-- кошироты, ![]() -- долготы. Разложение вектора
-- долготы. Разложение вектора
![]() по базису имеет вид:
по базису имеет вид:
Декартовы координаты вектора
![]() выражаются
через сферические координаты
выражаются
через сферические координаты
![]() следующим
образом:
следующим
образом:
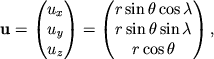
Единичные векторы
![]() в декартовых координатах имеют вид:
в декартовых координатах имеют вид:
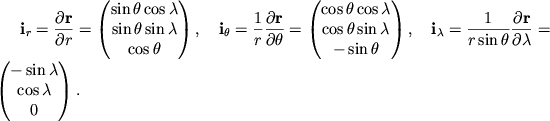
Преобразование между компонентами вектора в декартовом и сферическом базисе имеет вид:
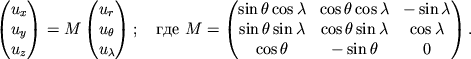
Обратное преобразование имеет вид:
<< A.2 Линейная алгебра | Оглавление | A.4 Элементы дифференциального и >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |
Мнения читателей [13]
Астрометрия
-
Астрономические инструменты
-
Астрономическое образование
-
Астрофизика
-
История астрономии
-
Космонавтика, исследование космоса
-
Любительская астрономия
-
Планеты и Солнечная система
-
Солнце