A.6 Сферические функции
Гравитационный потенциал ![]() во всех точках, находящихся на
поверхности и вне Земли, удовлетворяет уравнению Лапласа:
во всех точках, находящихся на
поверхности и вне Земли, удовлетворяет уравнению Лапласа:
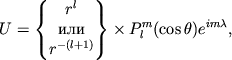
При ![]() получается уравнение Лежандра. В функциях
получается уравнение Лежандра. В функциях
![]() верхний индекс 0 обычно опускают.
верхний индекс 0 обычно опускают.
Определим сферические функции как
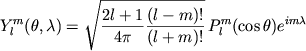
Полиномы Лежандра представляют собой решения уравнения Лапласа,
обладающие осевой симметрией. Очевидно, если ![]() , то сферические
функции
, то сферические
функции
![]() не зависят от долготы, и
называются зональными. Потенциал, разлагающийся только по
зональным функциям, можно записать в виде ряда по степеням
расстояния
не зависят от долготы, и
называются зональными. Потенциал, разлагающийся только по
зональным функциям, можно записать в виде ряда по степеням
расстояния ![]() от начала координат, коэффициентами которого
являются полиномы Лежандра. Они зависят только от полярного
расстояния
от начала координат, коэффициентами которого
являются полиномы Лежандра. Они зависят только от полярного
расстояния ![]() .
.
Присоединенные функции Лежандра являются ортогональными функциями, т.е.
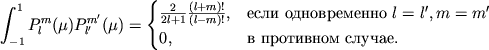
Каждая дважды дифференцируемая действительная функция
![]() , такая что
, такая что
![]() и определенная при
и определенная при
![]() и
и
![]() на поверхности сферы, может быть
разложена в сходящийся ряд
на поверхности сферы, может быть
разложена в сходящийся ряд
![$\displaystyle =\sum_{j=0}^{\infty}\left[\frac{1}{2}\alpha_{j0}P_j(\cos\theta) +\sum_{m=0}^j P^m_j(\cos\theta)(\alpha_{jm}\cos m\lambda +\beta_{jm}\sin m\lambda)\right] =$](https://images.astronet.ru/pubd/2003/06/11/0001190894/tex/formula1072.gif) |
||
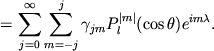 |
Коэффициенты разложения находятся следующим образом:
где
<< A.5 Криволинейные координаты | Оглавление | B. Основные термины >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |